利用回归直线方程预测

下面举一个利用回归直线方程进行预测的例子.

例2　某公司总经理认为，公司每年所获利润取决于当年投入的研究经费.表23.3提供了最近6年的有关数据.如果2014年公司投入研究经费1300万元，试预测该年公司的利润.

表23.3　公司利润与研究经费的关系

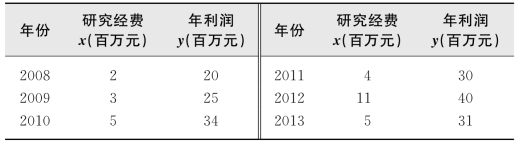
解　根据表23.3中的数据，计算出相应的xy和x2的值，于是得到表23.4.

表23.4　公司利润与研究经费关系的计算表

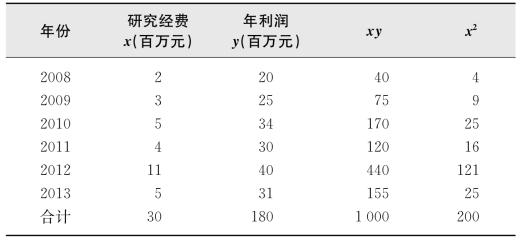
根据表23.4可得：

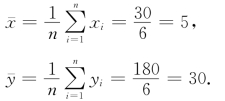
于是有

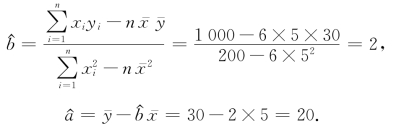
由上述方程可知，公司每年所获利润随着研究经费的增加而不断提高.

算得相关系数为

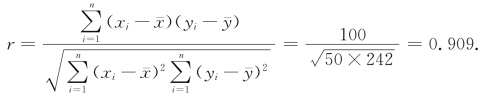
又n＝6，查相关系数检验表得

因为，所以变量x与y之间的线性关系显著，因此可用上述回归方程预测2014年该公司的利润为

＝20＋2×13＝46（百万元）.

具有相关关系的两个变量，散点的分布趋势不一定都是一条直线；更常见的是呈现为一条曲线.这时就需要观察分析它比较符合哪种类型的曲线，然后配出这条曲线的方程.常见的曲线类型有双曲线、指数曲线、对数曲线和幂函数曲线等.

可是，要确定曲线方程中的参数往往比较困难.我们可以通过变量变换将非线性关系转化成线性关系，然后再用最小二乘法求出参数的估计值.

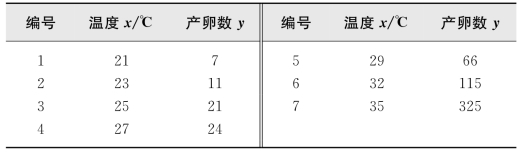
例3　一条红铃虫的产卵数y与温度x有关.经观察得到一组数据如表23.5所示.试求y关于x的回归方程.

表23.5　红铃虫产卵数与温度之关系

解　先根据表23.5的数据画出散点图，如图23.3所示.

可以看出，y与x之间的关系是非线性的；随着x的逐步增大，y先是缓慢增大，后来则是快速增大.即曲线先是缓慢上升，随后则快速上升.因此，可用指数曲线来描述红铃虫产卵数y与温度x之间的关系.于是有

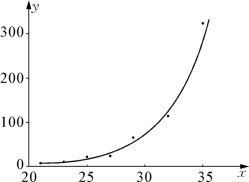
图23.3　红铃虫散点图

将上式两边同时取底数为e的对数，得

令u＝ln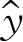，α＝lna；则有

u＝α＋bx.

于是将y与x之间的非线性回归问题转化为u与x之间的线性回归问题.将表23.5中的数据转换为表23.6中的数据.

表23.6　由表23.5变换得到的数据

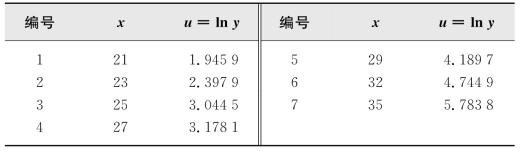
根据表23.6中数据可算得

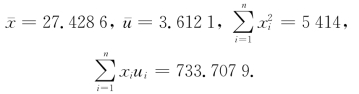
利用（23.4）式和（23.3）式可得

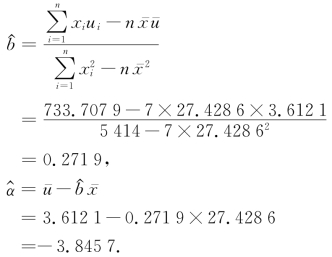
于是得到u关于x的回归方程

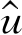＝-3.8457＋0.2719x.

因此y关于x的回归方程为

即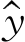＝0.02137e0.2719x.