网络的结构和学习算法

一、BP网络的结构和学习算法

BP网络是一种单向传播的多层前馈网络，由输入层、输出层和隐含层构成。在BP网络中，单隐含层网络的应用最为普遍，也叫三层前馈网络，其结构如图3.9所示。

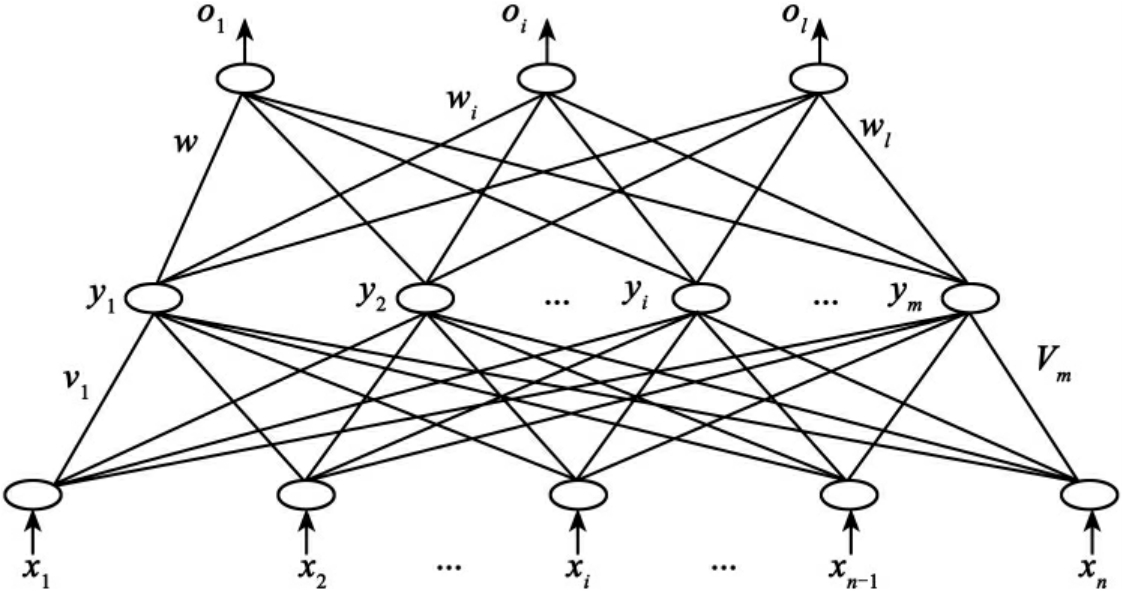
图3.9　三层BP网络结构

BP网络采用误差反向传播算法，这是一种基于梯度下降的δ规则学习算法。其基本思想是:整个网络的学习由信号的正向传播和误差的反向传播两个过程组成。在正向传播过程中，输入信号从输入层输入，经过网络的权值、阈值和神经元的传递函数作用后，从输出层输出。此时，如果输出层与期望层之间的误差大于规定值，则进行修正，转入误差反向传播阶段。误差反传是将输出误差，通过隐含层向输入层逐层返回，并将误差按“递度下降”原则“分摊”给各层神经元，并修改各层神经元的权值与偏差。以上两个过程是反复进行的，权值不断调整的过程，也就是网络训练过程，此循环一直进行到网络的输出误差减少到允许值，或到达设定的训练次数为止。其学习过程及步骤如:

如图3.9所示的三层网络结构，设

输入向量为X_k=(x₁，x₂，…，x_n);

期望输出向量为D_k=(d₁，d₂，…，d_l);

隐含层单元输入向量S_k=(s₁，s₂，…，s_m)，隐含层输出向量为Y_k=(y₁，y₂，…，y_m);

输出层单元输入向量L_k=(l₁，l₂，…，l_l)，输出层输出向量为O_k=(o₁，o₂，…，o_l);

输入层到隐含层之间的连接权v_ij，i=1，2，…，n，j=1，2，…，m;

隐含层到输出层之间的连接权w_jt，j=1，2，…，m，t=1，2，…，l;

隐含层各单元的输出阈值θ_j，j=1，2，…，m;输出层各单元输出阈值γ_t，t=1，2，…，l;

参数k=1，2，…，p。

第一步，初始化。给每个连接权值v_ij、w_jt，阈值θ_j与γ_t赋予区间(－1，1)内的随机数值。

第三步，输入样本X_k=(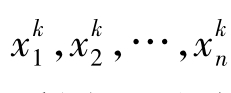)、连接权值v_ij和阈值θ_j，计算隐含层各单元的输入s_j，然后用s_j通过传递函数，计算隐含层各单元的输出y_j。

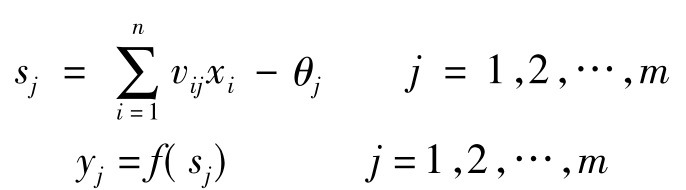
第四步，利用隐含层的输出y_j、连接权值w_jt、阈值γ_t，计算输出层各单元的输入L_t，然后利用传递函数，计算输出层各单元的响应O_t。

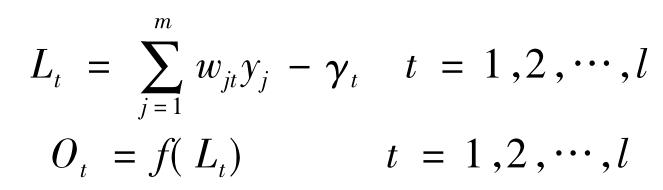
第六步，利用连接权w_jt、输出层的一般化误差c_t和隐含层的输出y_j，计算隐含层各单元的一般化误差。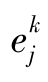

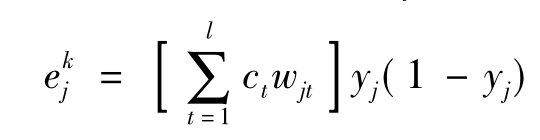
第七步，利用输出层各单元的一般化误差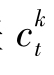，与隐含层各单元的输出y_j，来修正连接权w_jt、阈值γ_t。

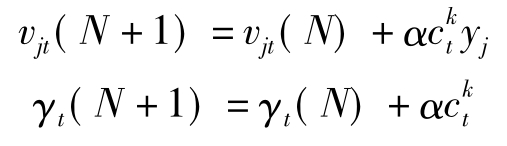
t=1，2，…，l，j=1，2，…，m，0＜α＜1

第八步，利用隐含层各单元的一般化误差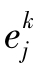，输入层各单元的输入X_k=(x₁，x₂，…，x_n)，来修正连接权值v_ij和阈值θ_j。

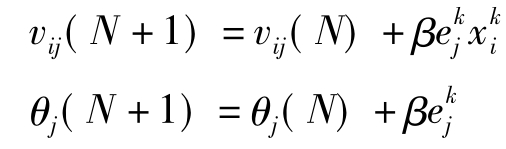
i=1，2，…，n，j=1，2，…，m，0＜β＜1

第九步，随机选取下一个学习样本向量，提供给网络，返回到步骤三，直到P个训练样本训练完毕。

第十步，重新从P个学习样本中随机选取一组输入和目标样本，返回步骤三，直到网络全局误差E，小于预先设定的一个极小值，即网络收敛。如果学习次数大于预先设定的值，网络就无法收敛。

第十一步，学习结束。

从上述分析可以看出，第七步至第八步为网络误差的“逆传播过程”，第九步至第十步则用于完成训练和收敛过程。