一、因素分析的基本原理[16]
因素分析方法的目的是要将各个观测变量表示成少数几个潜变量(公共因素)的线性加权之和。这样就可使原来用n个观测变量来描述个体特征转化为用少数几个更为本质的公共因素来描述,从而达到简化现象、揭示本质的目的。在数学上,由于观测变量(因变量)与潜变量(自变量)之间的线性关系是多样化的,采用不同的数学准则,就会得到不同的线性模型。通常采用两种不同的数学准则,因而因素分析一般有两种线性模型。
(一)全分量模型
从一组相关的观测变量中决定公共因素的第一种数学准则,是希望每次取得的一个公共因素的方差在观测变量的全部方差(或剩下的全部方差)中所占的比例最大。这个思想是由英国统计学家Pearson首先提出的,其方法由美国统计学家Hotelling完成。这种方法的线性模型是:
Z1i=a11F1i+a12F2i+…+a1nFni,
Z2i=a21F1i+a22F2i+…+a2nFni,
……
Zni=an1F1i+an2F2i+…+annFni.
i=1,2,…,n
也可简写为:
Zj=aj1F1+aj2F2+…+ajnFn.
j=1,2,…,n (3-1)
式(3-1)中的公共因素数等于观测变量数n。也就是各个观测变量用n个新的因素来线性表示。其中观测变量与因素都假定为标准化变量。这种模型称做全分量模型(full component model),这种分析方法称做主成分分析(principal component analysis)。
如果已知个体在n个因素上的得分,利用这种方法可精确地重新求得个体在n个观测变量上的得分,n个因素能够解释观测变量的全部方差。但是在实际使用中,人们总是只取少数几个对观测变量的方差贡献最大的为首因素。于是模型就成为:
Zj=aj1F1+aj2F2+…+ajmFm+αjej.j=1,2,…,n;m<n. (3-2)
式(3-2)常称做主成分分析模型。误差项αjej表示被忽略的几项的和。
(二)公共因素模型
从观测变量决定公共因素的第二种数学准则,是使抽取到的因素尽可能好地再生观测变量之间的相关,或者说能对观测变量之间的相关作出最好的分解。由这种数学准则导出的数学模型就是传统的或经典的公共因素模型(common factor model):
Zj=aj1F1+aj2F2+…+ajmFm+djUj.j=1,2,…,n;m<n. (3-3)
在公共因素模型中,因素被划分为两部分,为首部分的m个因素称做公共因素,每一个公共因素至少对两个或两个以上的观测变量有影响;剩下的一个因素U只对相应的一个观测变量有影响,所以称做唯一性因素(unique factor)。公共因素模型表示n个观测变量的各个变量均可表示成m个公共因素和一个唯一性因素的线性加权之和。其中公共因素用以解释观测变量之间的相关,唯一性因素用以解释观测变量除去公共因素的影响以后所剩下的那部分方差。不失为一般性,在模型(3-3)中观测变量Z、公共因素F和唯一性因素U都假定为标准化标量,它们的数学期望为0,标准差为1;而且n个唯一性因素Uj(j=1,2,…,n)之间互相独立,各个唯一性因素Uj与各个公共因素Fp(p=1,2,…,m)之间也互相独立。
(三)因素的度量
因素分析可以划分为两类问题,一类问题研究怎样以一组假设的因素来线性地表示观测变量;另一类问题则是研究怎样以已知的观测变量来线性地表示假设的因素结构。我们以主成分因素的度量为例来说明第二类问题的解决过程。
在实际分析中,通常采用的是式(3-2)的模型,即只取前m个影响大的分量,这时式(3-2)的矩阵表达式是:
Zn×1=An×mfm×1 (3-4)
其中Zn×1是观测资料矩阵,An×m是公共因素系数矩阵,fm×1是得分矩阵,n为变量数。
通过换算,因素分数可由下式求取:
fm×1=(A'm×nAn×m)-1A'm×nZn×1 (3-5)
因为A'm×nAn×m=Λm×m,Λm×m是由相关矩阵Rn×n的前m个特征根为对角元而构成的对角阵,所以:
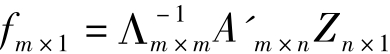
设fp是向量f的第p个分量,则:
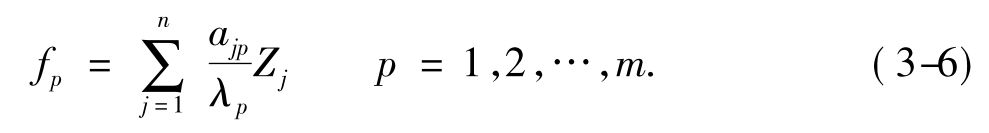
式(3-6)是一个代数表达式,不存在统计估计的问题。方程中的系数是由相应的主成分的负荷除以该主成分的特征根得到的。
主成分的另一个重要性质是任何旋转主成分也能方便地用变量的线性组合来表示。若An×m是主成分的初始负荷矩阵,Tn×m是交换矩阵,则旋转主成分的负荷矩阵:
Bn×m=An×mTm×m
变量的新的解是:
Zn×1=Bn×mgm×1
其中gm×1表示不同于原列向量fm×1的旋转主成分的列向量。类似于求取fm×1的表达式的方法可求得:
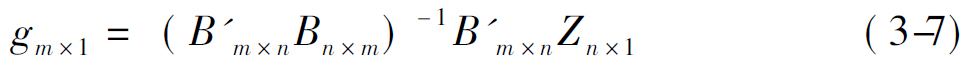
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。














