因子分析模型（卫海英，）

1．因子分析模型（卫海英，2002）

（1）初始因子模型

例：为了了解学生的知识和能力，随即抽取80名学生，每人回答30题，问题涉及面很广，但总的来讲，主要是测试学生的语文水平、数学推导、艺术修养、历史知识、生活常识5个方面，每个方面称为公共因子。可以设想每个学生的成绩X_i，其标准化成绩x_i＝（X_i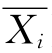－）／S_i（i＝1，2，…，80），上述5个公共因子的线性函数表示为

其中：F₁，F₂，…，F₅为5个公共因子，它们是不可测的，只是一个抽象的概念。其系数a_i1，a_i2，…，a_i5叫做因子负荷（或载荷、权数），表示第i个学生在5个方面的能力，μ_i是第i个学生的知识能力不能被5个因子包括的部分，称为特殊因子，假定μ_iN（0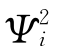）。因子分析的任务就是要估计F_j的个数及a_ij和方差，然后给因子F_j一个合理的解释。若难以找到合理解释，需进一步作因子旋转，以求旋转后能得到合理的解释。

将问题一般化，则因子分析的一般模型可写成：设某问题中的测量指标有X₁，X₂，…，X_p，其标准化指标为x_i（i＝1，2，…，p），各指标均受m（m＜p）个因子支配，同时每个指标还受一个特殊因子的制约，于是，标准化变量x_i可用因子F和特殊因子u线性表示，即

此模型有两个特点：一是模型不受量纲的影响；二是因子负荷不是唯一的。这种非唯一性从表面上看是不利的，但通过因子轴的旋转，可使新的因子更具有鲜明的实际意义。

（2）旋转后的因子模型

当初始因子模型（公式5）求得后，一般来说，载荷矩阵的结构比较复杂，不易于因子的解释，若用公共因子线性组合表达标准化指标则更容易做出有意义的解释，即：使得矩阵A中各列元素向更小（0）和向更大（1）两极分化，但保持同一行中各元素平方和（公因子方差）不变，实现这一目的的变换方法叫因子轴的旋转。通过因子轴的旋转，可求得对公共因子命名和解释的结果。设从公共因子F旋转到公共因子G，则公式5变为

式中的b_ij仍称为因子载荷。

（3）因子得分模型

无论是公式5还是公式6的因子模型，都是将指标表示为公因子的线性组合。在因子分析中，还可以将公因子表示为指标的线性组合，这样就可以从指标的观测值估计各个公共因子的值，此值称为因子得分。即

（4）模型的有关假设

①线性假设。模型为线性模型。

②独立性假设。各特殊因子之间以及特殊因子与所有公因子之间均相互独立。

③公因子都是均数为0、方差为1的独立正态随机变量，其协方差矩阵为单位矩阵。