因子分析模型

二、因子分析模型

（一）基本原理

设m个可能存在相关关系的测试变量Z₁，Z₂，…，Z_m含有p个独立的公共因子F₁，F₂，…，F_P（m≥p），测试变量Z_i含有独特因子ε_i（i＝1，2，…，m），诸ε_i间互不相关，且与F_j（j＝1，2，…，p）也互不相关，每个Z_i可由p个公共因子和自身对应的特殊因子ε_i线性表出⁽¹⁷⁾：

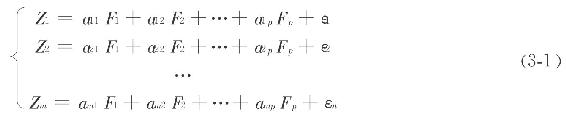
用矩阵表示为：

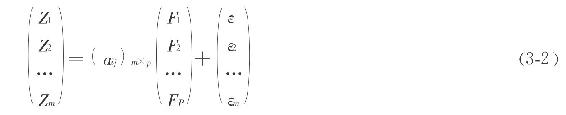
模型简记为：

满足：（1）p≤m；

（2）cov（F，ε）＝0（即F与ε是不相关的）；

（3）E（F）＝0，cov（F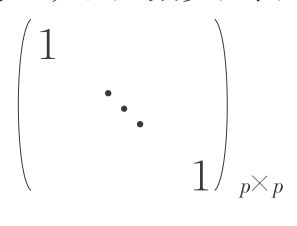）＝＝I_p，即F₁，F₂，…，F_P不相关，且均值皆为0，方差皆为1；

（4）E（ε）＝0，cov（ε）＝I_m，即ε₁，ε₂，…，ε_m不相关，且都是标准化的变量，假定Z₁，Z₂，…，Z_m也是标准化的，但并不相互独立。

式（3-3）中的A称为因子载荷矩阵，其元素（即式（3-1）中各方程的系数）a_ij表示第i个变量Z_i在第j个公共因子F_j上的载荷，简称因子载荷。如果把Z_i看成p维因子空间的一个向量，则a_ij表示Z_i在坐标轴F_j上的投影，表示第i个原始变量与第j个因子变量的相关系数。a_ij的绝对值越大，则Z_i与F_j的关系越强。

因子分析的目的就是通过式（3-1）或（3-2）以F代Z，由于一般有p＜m，从而达到简化变量维数的目标，这样既可减轻收集信息的工作量，且各综合指标代表的信息又不会重叠。

（二）基本步骤

围绕浓缩变量提取因子的核心目标，因子分析通常包括以下四个主要步骤：

（1）相关性判定。借助变量的相关矩阵、KMO检验⁽¹⁸⁾和Bartlett检验⁽¹⁹⁾方法进行分析，相关矩阵是因子分析直接要用的数据，根据结果进一步判断待分析的原始变量是否适合作因子分析。

（2）提取因子。将变量综合成少数几个因子（称为公共因子）是因子分析的核心思想，在这一步要确定公共因子的形式和公共因子求解的方法。

（3）因子旋转。建立因子分析模型的目的不仅要找出公共因子，更重要的是要知道每个公共因子的明确意义，这一步的目的是利用旋转方法使因子变量具有可解释性。

（4）计算因子得分。因子得分是各个因子在每个样本上的得分值，有了因子得分值就可以在其他的分析中使用这些因子⁽²⁰⁾。