模型自相关的消除

模型自相关的消除_劳动力市场分割与农民工就业实证研究

1． 模型的自相关检验

对模型(5－12)，用杜宾—瓦尔森(Durbin－Watson)d检验如下:

d=0．492

n=21，k=3，假定显著水平α=5%

从D－W表中可以查到dl=1．026，du=1．669

因为d=0．492＜dl=1．026，根据D－Wd检验判定规则，可以得出结论: 在模型(5－12)中误差项中存在正的自相关。这与古典线性回归模型第四条基本假设: 任意两个误差项之间不相关，即cov(εit，εjt) =0，i≠j，是不符合的。

2． 模型存在自相关的后果

当模型(5－12)存在自相关时，OLS估计量虽然是线性的和无偏的，但不是最优线性无偏估计量(BLUE)，OLS估计量的方差是有偏的，从而使t值不准确，有时导致t检验不可靠。在具体应用中，有必要采取一些补救措施对自相关加以消除。

3． 自相关的消除及游程检验

由于序列相关可能导致非常严重的后果，并且进一步检验的成本很高，因此应该采取一些补救措施。

对模型yt=β0+β1x1t+β2x2t+β4x4t+εt(5－13)

假设误差项服从马尔可夫一阶自回归AR(1)过程:

εt=ρεt－1+νt－1≤ρ≤1

其中，ν满足CLRM的基本假定: E(υt) =0，var(υt) =σ2υ， υt～N(0，σ2υ)，cov(υt，υt－m) =0，σ2υ是常量，m为任一常数，ρ是可知的，可以通过以下方法计算获得。

杜宾—瓦尔森(Durbin-Watson)d统计量，定义为:

对模型(5－13)进行变换，使得变换后模型的误差项是序列独立的，然后再用OLS方法进行估计，则可得到最优线性无偏估计量(BLUE)，这种方法称之为广义最小二乘法(GLS方法)。

将模型(5－13)中的变量滞后一期，记为:

yt－1=β0+β1x1，t－1+β2x2，t－1+β4x4，t－1+εt－1(5－14)

将方程(5－14)的两边同时乘以ρ，得到:

ρyt－1=ρβ0+ρβ1x1，t－1+ρβ2x2，t－1+ρβ4x4，t－1+ρεt－1 (5－15)

方程(5－14)与方程(5－15)相减，考虑到εt=ρεt－1+νt，得:

yt－ρyt－1=β0×(1－ρ) +β1×(x1t－ρx1，t－1) +β2×(x2t－ρx2，t－1) +β4×(x4t－ρx4，t－1) +νt(5－16)

将方程(5－16)改写为:

y*t=β*0+β1x*1t+β2x*2t+β4x*4t+νt(5－17)

其中:

y*t=yt－ρyt－1t=2，3，…，T

x*1t=x1t－ρx1，t－1t=2，3，…，T

x*2t=x2t－ρx2，t－1t=2，3，…，T

x*4t=x4t－ρx4，t－1t=2，3，…，T

β*0=β0×(1－ρ) t=2，3，…，T

对模型(5－13)，当t=1时，进行Prais-Winsten变换:

y1=β0+β1x11+β2x21+β4x41+ε1(5－18)

方程(5－18)乘以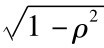得:

方程(5－19)改写为:

y*1=β*0+β1x*11+β2x*21+β4x*41+υ1(5－20)

其中:

结合方程(5－17)和方程(5－20)得到:

根据上述方法，将表5－6的数据变换成如表5－11所示。

用SPSS软件，运用GLS方法，得到如下结果:

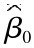=8282．795

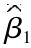=－5635．812

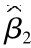=－6578．787

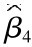=－3．836

表5－11 表5－6变换后的数据(ρ=0．754)

因此，消除自相关后，模型(5－12)优化成模型(5－21):

s．e． =(430．626) (1164．564) (2215．242) (8．940)

t=(19．234) ( －4．839) ( －2．970) (0．429)

p值=(0．000) (0．000) (0．009) (0．674)

R2=0．890

F值为43．128，分子自由度d．f．为3，分母自由度d．f．为16

Durbin－Watson的d值为0．773

模型(5－21)与模型(5－12)相比，有两个方面表现得较优:一是劳动力市场单位性质分割程度变量的估计参数β4＜0，说明农民工就业与劳动力市场单位分割负相关。二是模型的Durbin－Watson的d值提高到0．773，自相关现象在一定程度上得到消除。当然R2和F值有点降低，但并不妨碍对模型的定性解释和F检验的通过。

d统计量值为0．773，按照杜宾—瓦尔森(Durbin－Watson)d检验法，可知道模型(5－21)仍然存在自相关。但有的文献认为，从变换后的回归中所计算的d统计量可能并不适合于自相关的检验，因为如果将它用作这一目的，就表明初始误差项并不遵循AR (1)，比如说它可能遵循AR(2)。

游程检验是非参数检验，可以用来检验变换后的模型是否存在自相关现象。现在用游程检验来验证。

原假设: 模型(5－13)中ε是随机的。

备择假设: 模型(5－13)中ε不是随机的，即存在自相关。

用SPSS软件，记录模型(5－21)中不同观察值误差项的符号依次为:

( －)( －)( +)( +)( +)( +)( +)( +)( +)( －)( －) ( －)( －)( －)( +)( －)( +)( +)( +)( +)

观察值的总个数N=21

正的误差项的个数N1=12

负的误差项的个数N2=7

游程个数k=6

查史威德—艾森哈特(Swed－Eisenhart)临界值表，显著性水平为5%时的临界的游程值为6。实际的游程个数等于史威德—艾森哈特临界值，因此拒绝零假设，也就是说模型(5－21)中的数据仍然存在自相关。

当然我们可以继续对模型进行上述变换或采取其他措施，直到自相关现象消失为止。为了节省篇幅，本书对模型的优化到此为止。