利用上面得到的数据,分别将内容获益值、过程获益值和PISA数学测评成绩作为自变量,将中考数学测评成绩作为因变量,进行线性回归分析。这里采用向前回归方式,运用SPSS 19.0所得回归结果如表7-14所示。
表7-14 内容、过程获益值和PISA数学测评成绩对中考数学测评成绩的回归分析结果(一)输入/移去的变量b

a.已输入所有请求的变量;
b.因变量:中考数学测评成绩。
模型汇总
(续表)
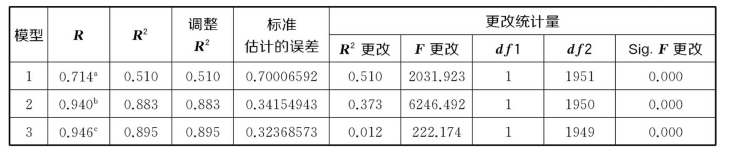
a.预测变量:(常量)PISA数学测评成绩;
b.预测变量:(常量)PISA数学测评成绩,过程获益值;
c.预测变量:(常量)PISA数学测评成绩,过程获益值,内容获益值。
从表7-14可以看到,PISA数学测评成绩只能解释中考数学测评成绩差异的51%,而过程获益值变量的加入,能增加37.3%的解释率,在此基础上继续加入内容获益值变量,解释率进一步增加1.2%。两个获益值能共同解释中考数学测评成绩差异的38.5%。在回归分析中,将过程获益值先于内容获益值纳入回归分析。从统计意义上,过程获益率对中考数学测评成绩的差异解释程度要比内容获益率高。PISA数学测评的成绩、过程获益值和内容获益值三个变量共同能解释了中考数学测评成绩差异的89.5%。对依次加入上述三个变量的三种模型进一步分析,所得回归结果如表7-15所示。
表7-15 内容、过程获益值和PISA数学测评成绩对中考数学测评成绩的回归分析结果(二)Anovad
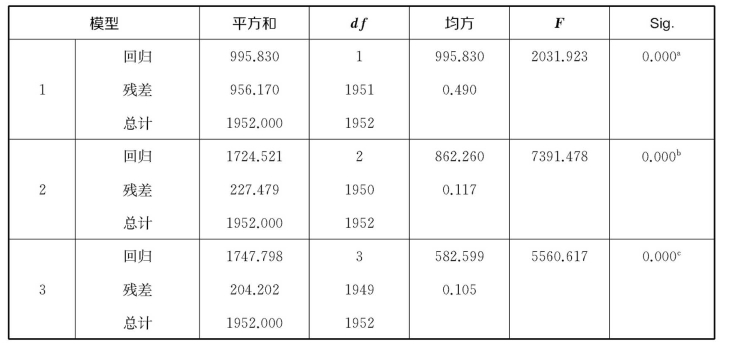
a.预测变量:(常量)PISA数学测评成绩;
b.预测变量:(常量)PISA数学测评成绩,过程获益值;
c.预测变量:(常量)PISA数学测评成绩,过程获益值,内容获益值;
d.因变量:中考数学测评成绩。
系数a
(续表)
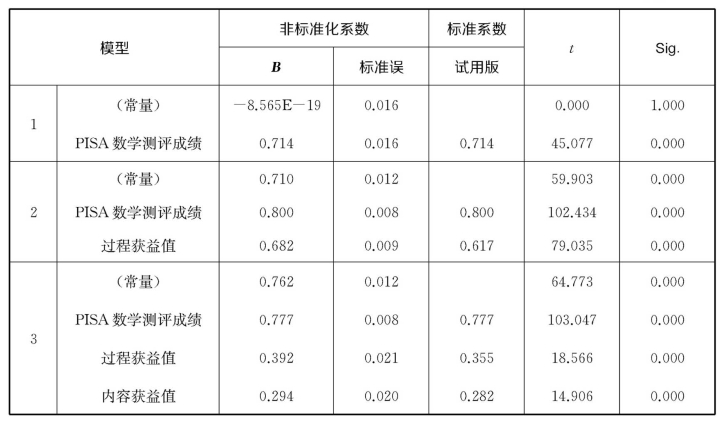
a.因变量:中考数学测评成绩。
从表7-15可以看到,当过程获益值和内容获益值共同作为解释变量时,PISA数学测评成绩每提升1个单位,中考数学测评成绩可提升0.777个单位;过程获益值每提升1个单位,中考数学测评成绩可提升0.392个单位;内容获益值每提升1个单位,中考数学测评成绩可提升0.294个单位。对中考数学测评成绩来说,两个数学测评在过程维度上差异的影响,明显高于在内容领域上差异的影响。同时,从显著性检验结果来看,三个自变量的加入,结果显示有显著性,表示还可有其他变量能够解释中考数学测评成绩。
从上述分析中可以看到,在内容领域和过程维度上,中考数学测评与PISA数学测评的差异性,对中考数学测评成绩个体差异的解释程度是很大的。同时可以看出,过程维度上的差异在对两种测评结果差异的解释率上要高出内容领域上的差异。实际上过程维度上的差异性,在两者的试题分布表中可以直接体现出。从PISA数学测评的过程维度看中考数学测评的试题分布,可以发现缺失了问题解决的表述,也缺乏解释/评估。而这两者在中考数学测评的目标中是有要求的,如对文字语言、图形语言、符号语言进行相互转化,对问题解决的结果进行合理解释等。这反映出在该中考数学测评中对问题解决测评的缺乏,以及在试题表征上的不足,也在一定程度上反映出目前教学中的实际状况——对问题解决教学的认识不足或不完整。
以上分析进一步促使我们慎重对待目标分析框架中内容和过程两个方面的设计。设计的差异会直接影响最后的成绩,以及群体差异的解释率。对于中考数学测评这种高利害性的测评而言,这是值得重点关注的。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
















