不同类型国际品牌价值驱动因素研究

第三节　不同类型国际品牌价值驱动因素研究

由本书的国际品牌新概念框架可知，国际品牌可分为全球品牌、双区域国际品牌、区域国际品牌和天生国际品牌，表明国际品牌成长是一个持续动态发展的过程。对于不同成长阶段国际品牌的价值的驱动因素是否相同也是一个需要深入研究的问题。鉴于天生国际品牌样本量太小，本节只对全球品牌、双区域国际品牌和区域国际品牌的价值驱动因素进行研究。

一、不同类型国际品牌样本的探索性因子分析

1.不同类型国际品牌样本的选取

本节将收集的国际品牌样本总体根据国际品牌类型分为3个子样本:全球品牌样本、双区域国际品牌样本和区域国际品牌样本，3个不同子样本的观察值分别为40、61和162，如表6－34所示。

2.不同类型国际品牌子样本数据的因子分析适用性检验

利用SPSS 15.0软件对3个不同类型国际品牌的子样本数据进行因子分析适用性检验，分别得到4个自变量的相关关系矩阵，如表6－31、6－32和6－33所示，来自不同行业的许多变量之间存在着高度相关，大多数变量之间的相关系数大于0.3，表明这三个不同的样本数据都适合做因子分析。

表6－31　　　　　全球品牌样本的相关系数矩阵

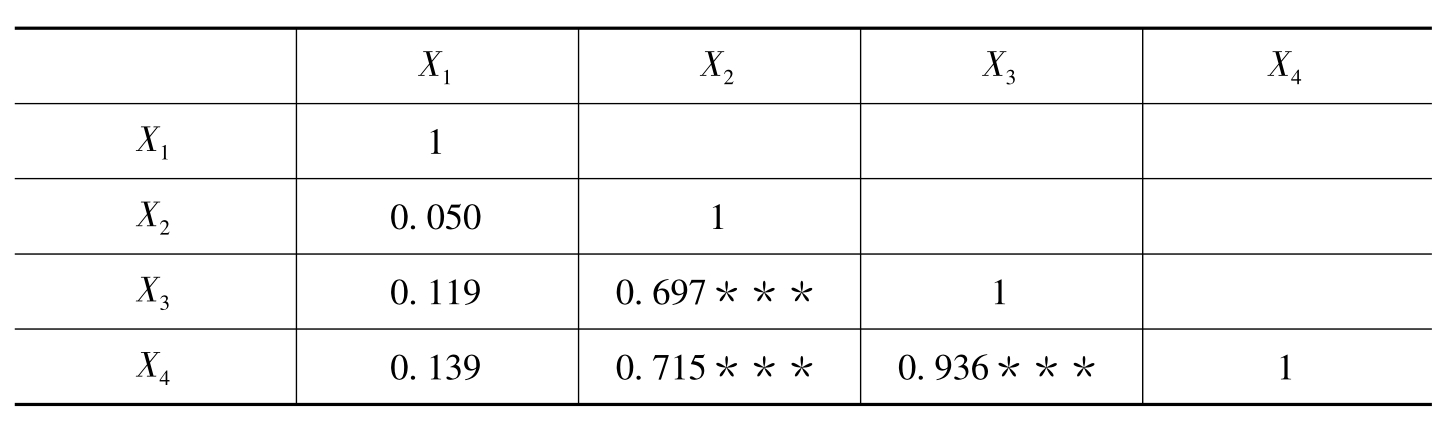
注:＊＊＊表示在1%水平上显著，＊＊表示在5%水平上显著，*表示在10%水平上显著

表6－32　　　　　双区域国际品牌样本的相关系数矩阵

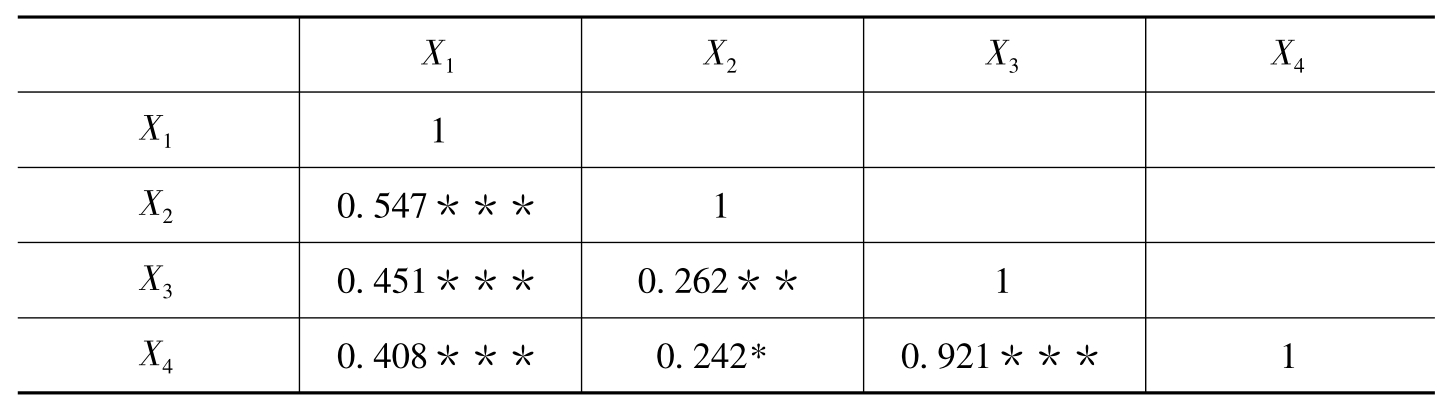
注:＊＊＊表示在1%水平上显著，＊＊表示在5%水平上显著，*表示在10%水平上显著

表6－33　　　　　区域国际品牌样本的相关系数矩阵

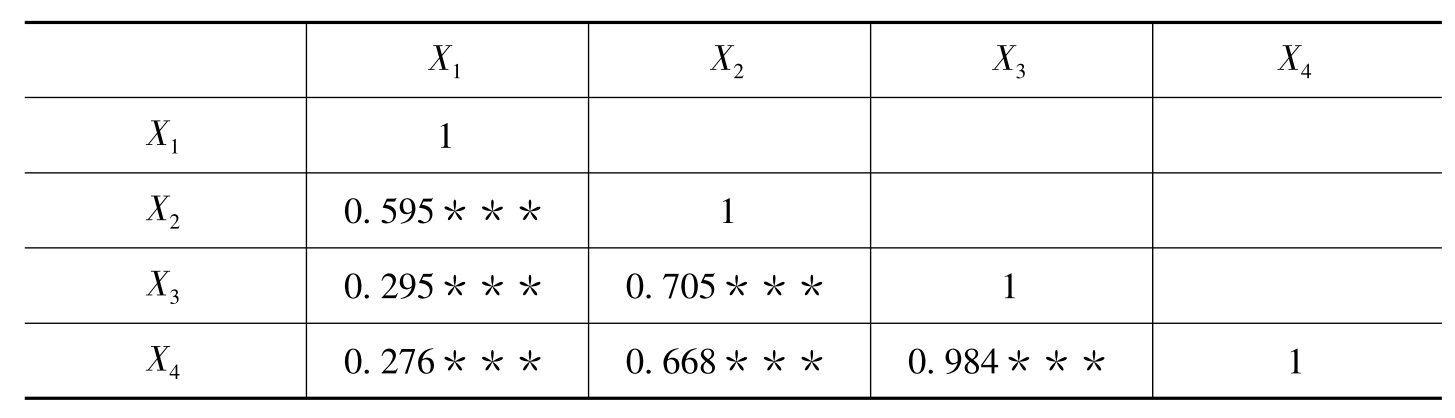
注:＊＊＊表示在1%水平上显著，＊＊表示在5%水平上显著，*表示在10%水平上显著

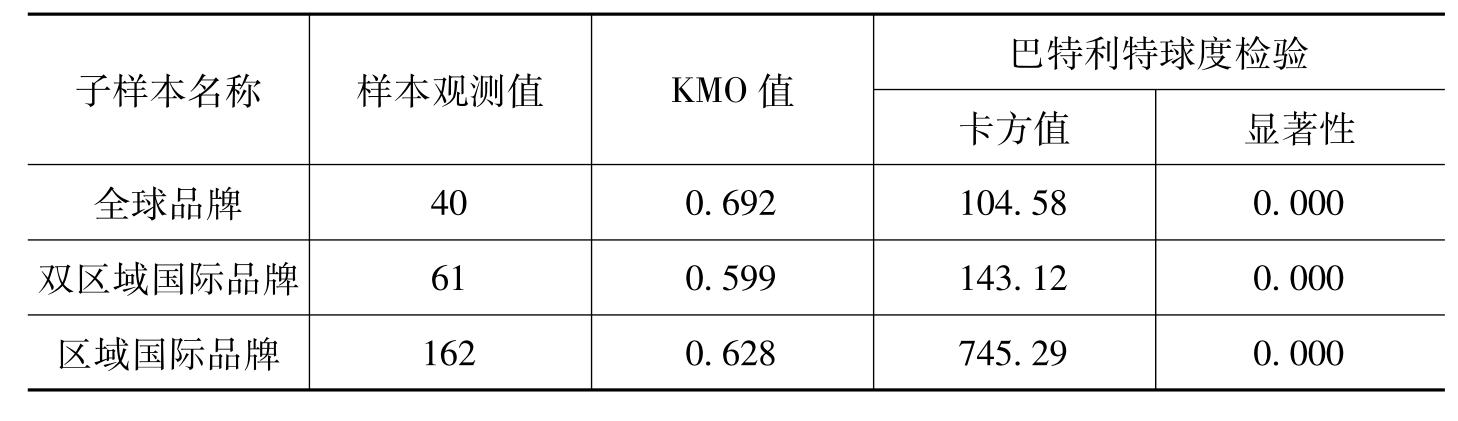
分别对3个不同类型国际品牌的样本数据进行KMO与巴特利特球度检验，验证结果如表6－34所示。全球品牌、双区域国际品牌和区域国际品牌样本数据的KMO值分别为0.692、0.599、0.628，都大于0.5，表明这3个子样本数据适合进行因子分析。根据巴特利特球度检验显示，全球品牌、双区域国际品牌和区域国际品牌样本数据的卡方统计值分别为104.58、143.12、745.29，显著性水平P＜0.01，巴特利特球度检验显示变量之间具有相关性。可见，3个不同类型国际品牌的子样本数据均通过两项验证性检验，表明3个子样本数据适合进行因子分析。

表6－34　　　　　不同类型国际品牌样本的因子验证分析指标

二、全球品牌价值驱动因素分析

1.探索性因子分析评估结果分析

利用SPSS 15.0采用主成分分析法提取公共因子，分析结果如表6－36所示。其中，只有1个公共因子的特征值大于1，方差累积贡献率为64.78%，没有达到公共因子累计方差超过85%的标准，不能很好地反映全部变量指标信息。因此，将进一步进行因子旋转分析，利用最大方差正交旋转法进行因子旋转，得到旋转后因子载荷矩阵，如表6－36所示。

表6－35　　　　　全球品牌的相关矩阵的特征值、方差贡献率和累积贡献率

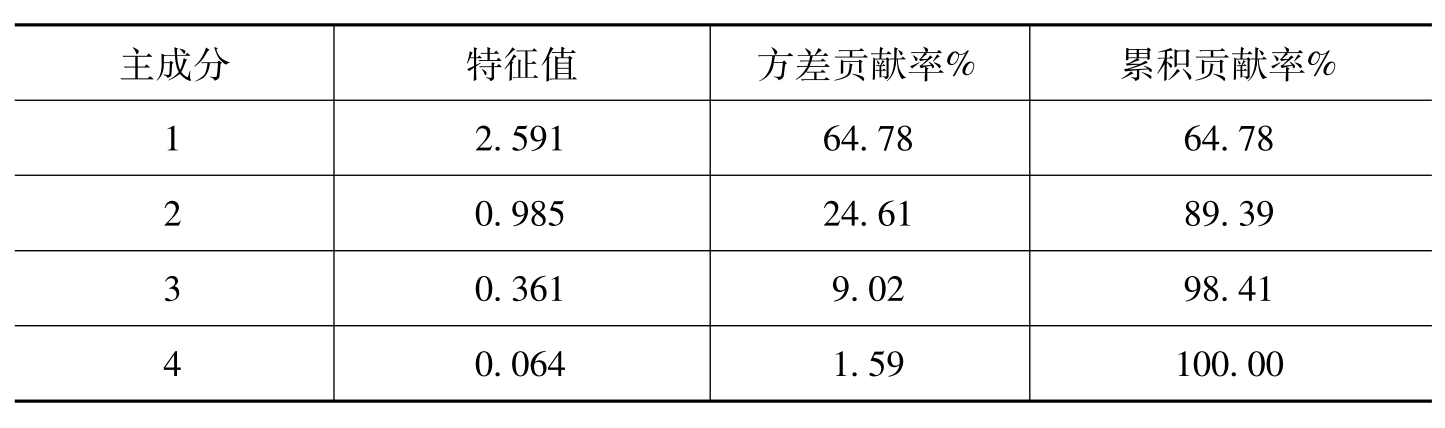
注:利用主成分分析法提取公共因子

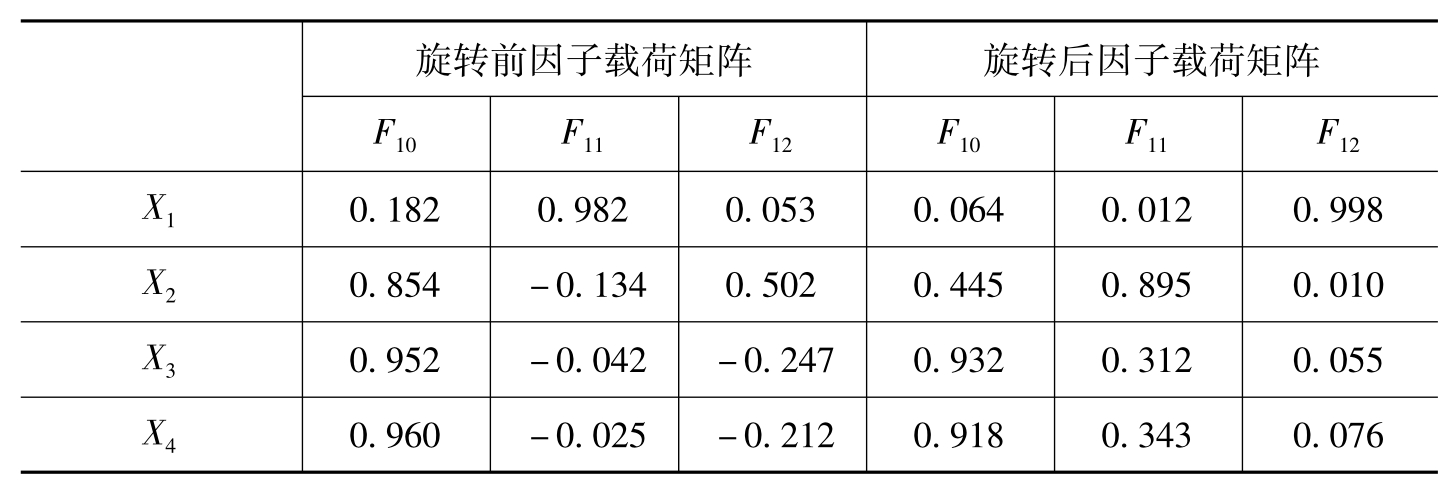
由表6－36旋转前因子载荷矩阵可知，直接提取三个公共因子，不能赋予三个公共因子合理的经济解释。为了解决各个公共因子的典型代表变量不很突出的问题，还将进行因子旋转分析。利用最大方差正交旋转法进行因子旋转，得到旋转后因子载荷矩阵，如表6－36所示。其中，F₁₀在X₃(营业利润)和X₄(净利润)上的载荷较大，载荷量分别为0.932和0.918，这两个变量基本上反映了全球品牌为企业带来的市场业绩，将F₁₀命名为市场业绩因子; F₁₁在X₂(研发费用)上的载荷较大，载荷量为0.895，这个变量基本上反映了全球品牌的产品研发设计能力，将F₁₁命名为产品研发设计能力因子; F₁₂在X₁(广告费用)上的载荷最大，载荷量为0.998，反映了全球品牌的营销沟通能力，将F₁₂命名为营销沟通能力因子。

表6－36　　　　　全球品牌样本旋转前后因子载荷矩阵

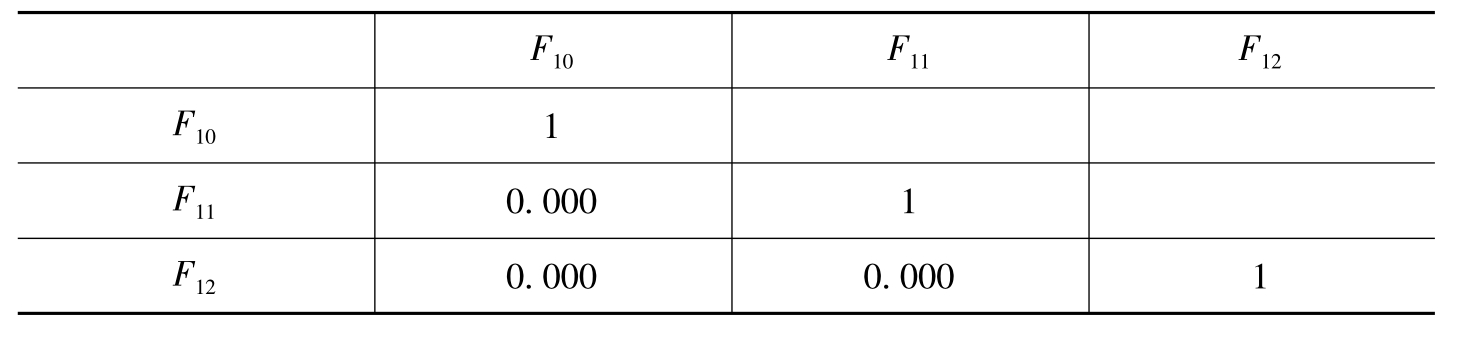
由表6－37估计回归因子分数的协方差矩阵(即三个公共因子间的相关矩阵)可知，样本数据利用最大方差正交旋转法进行因子旋转后，三个

公共因子F₁₀、F₁₁和F₁₂是完全不相关的，表明旋转后得到的结果可靠。

表6－37　　　　　估计回归因子分数的协方差矩阵

2.计算公共因子得分

因子分析的目的是减少变量个数，以便在进一步分析中用较少的公共因子代替原有变量进行数据建模。由于公共因子是不可观测的隐变量，需通过计算因子得分给提取的公共因子赋值。因子得分求解的过程就是以原始变量的线性组合来表示公共因子，因子得分系数是原始变量的权重。利用回归法估计因子得分，因子得分函数是:

F_j=β_j1 X₁+β_j2 X₂+…+β_jp X_p(p= 1，2，3，4，5; j= 1，2，3)上式中，β为回归法得出的因子得分系数，具体的因子得分系数如表6－38所示。

表6－38　　　　　全球品牌的因子得分系数

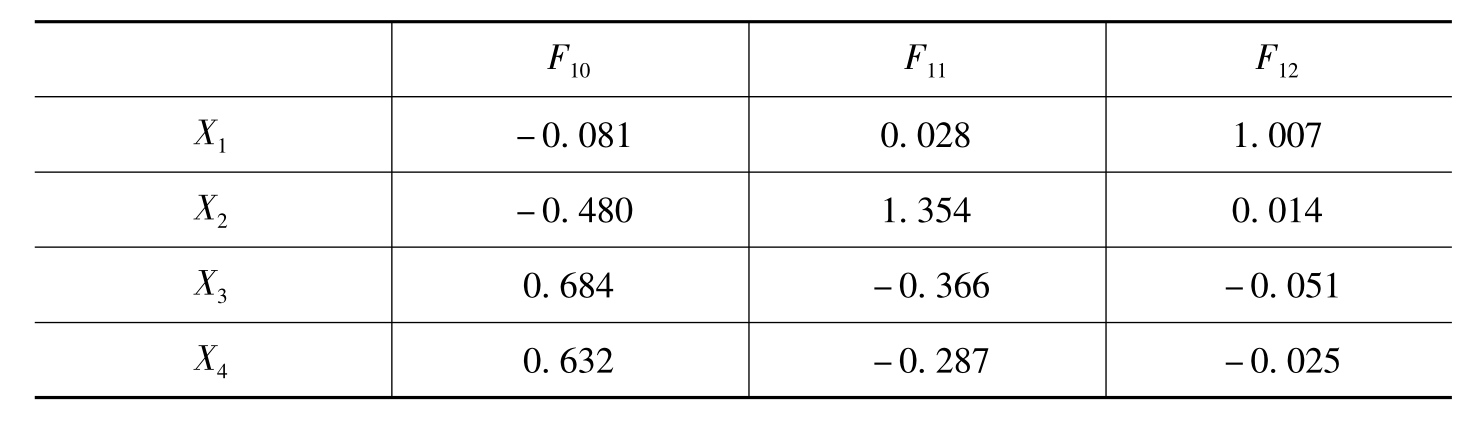
由此可得到市场业绩因子(F₁₀)、产品研发设计能力因子(F₁₁)、营销沟通能力因子(F₁₂)三个公共因子得分的计算公式为:

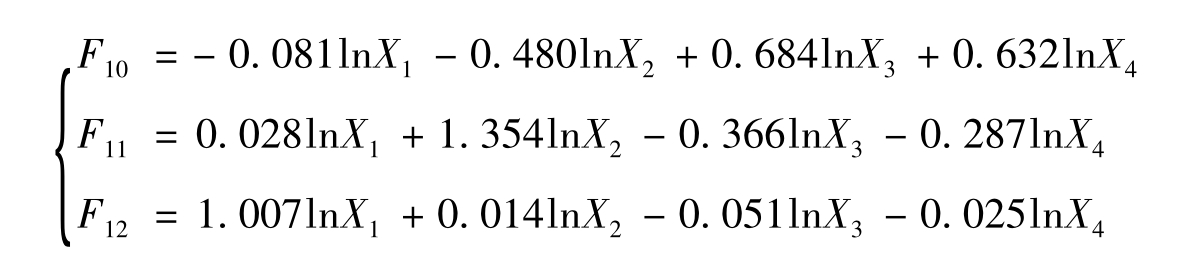
(公式4)

这三个公共因子是否是全球品牌价值的驱动因素，对全球品牌价值成长的影响程度是多少，尚需进行回归分析予以验证。

3.研究假设

根据探索性因子分析结果，全球品牌价值的驱动因素包括三个方面:企业市场业绩、产品研发设计能力和营销沟通能力。这三个驱动因素是否对全球品牌价值的成长具有显著影响，需要进一步进行深入分析。因此，提出如下假设:

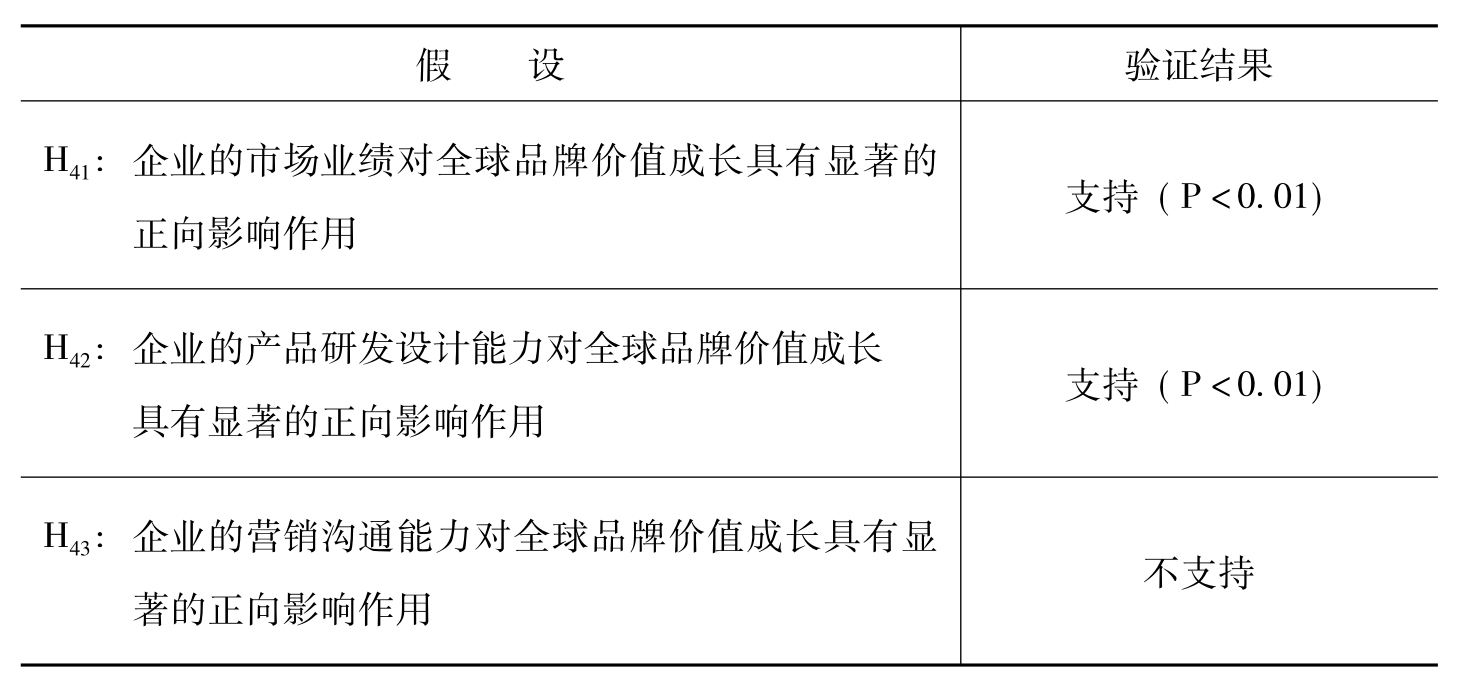
H₄₁:企业的市场业绩对全球品牌价值成长具有显著的正向影响作用。

H₄₂:企业的产品研发设计能力对全球品牌价值成长具有显著的正向影响作用。

H₄₃:企业的营销沟通能力对全球际品牌价值成长具有显著的正向影响作用。

根据上述提出的研究假设，建立多元回归方程，如下所示:

ln Y₄=β₄₀+β₄₁ F₁₀+β₄₂ F₁₁+β₄₃ F₁₂+ε₄(模型4)

Y₄表示全球品牌价值;

F₁₀表示市场业绩驱动因子;

F₁₁表示产品研发设计能力驱动因子;

F₁₂表示营销沟通能力驱动因子。

4.实证分析过程

由于F₁₀、F₁₁和F₁₂是通过探索性因子分析得到的公共因子，不能直接获得观测值，因此，它们的取值利用公式4计算得到，即因子得分。国际品牌价值(Y₄)的数据来自2001—2008年Interbrand“全球品牌100强”发布的全球品牌价值。F₁₀、F₁₁和F₁₂的取值是利用自变量观测值的对数值根据公式4计算得到。为了保证处理数据的一致性，将因变量的取值也取对数。

利用SPSS 15.0对多元回归模型的变量进行相关分析，计算各个变量之间的皮尔森相关系数，检验各个变量之间的相关关系。如表6－39所示，3个自变量F₁₀、F₁₁和F₁₂与ln Y₄有显著正相关关系。由表6－37估计回归因子分数的协方差矩阵可知，3个自变量之间是完全不相关的，因此，自变量之间不会存在多重共线性的问题，可以直接进行多元回归分析。

表6－39　　　　　全球品牌样本各变量的皮尔森相关系数矩阵和描述性统计分析

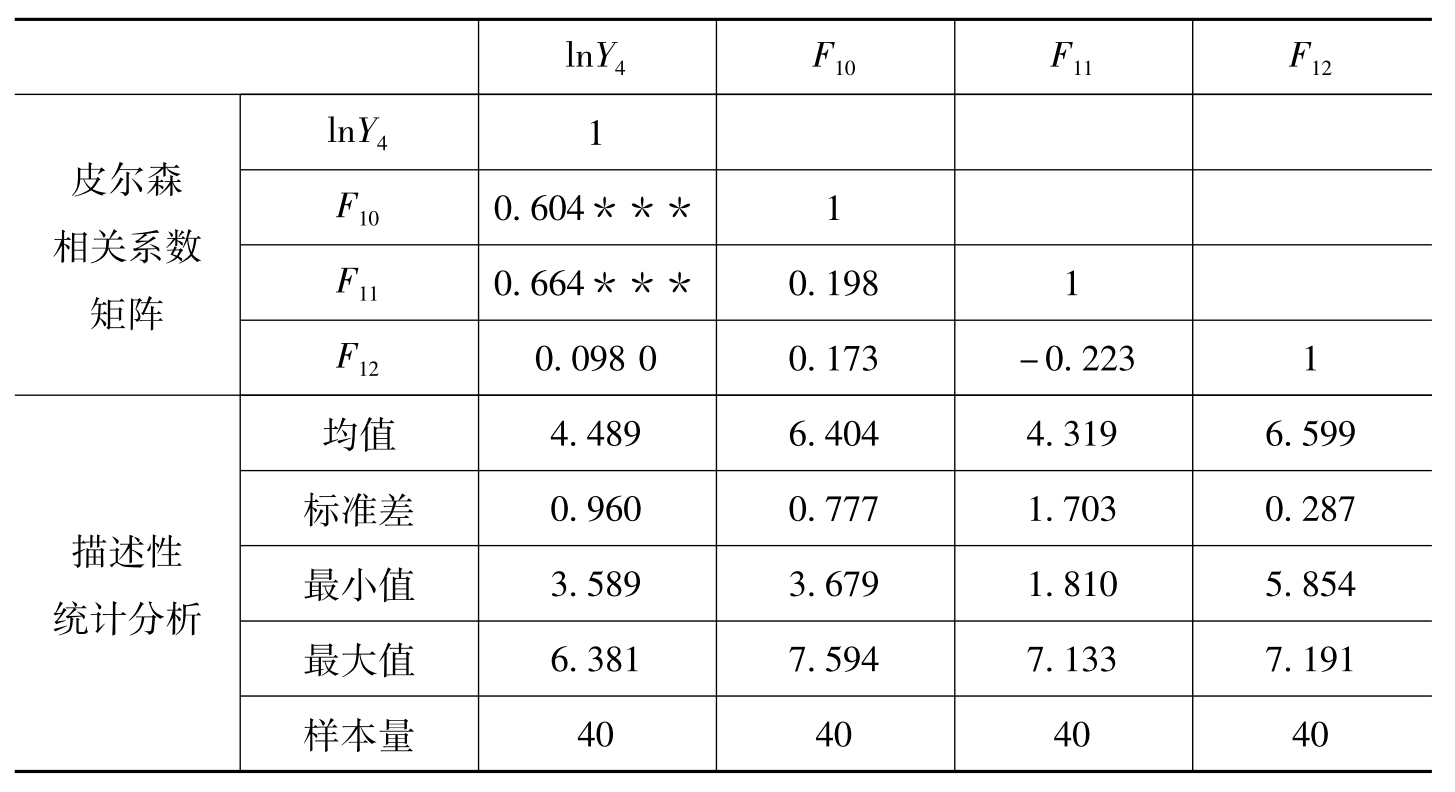
注:＊＊＊表示在1%水平上显著，＊＊表示在5%水平上显著，*表示在10%水平上显著

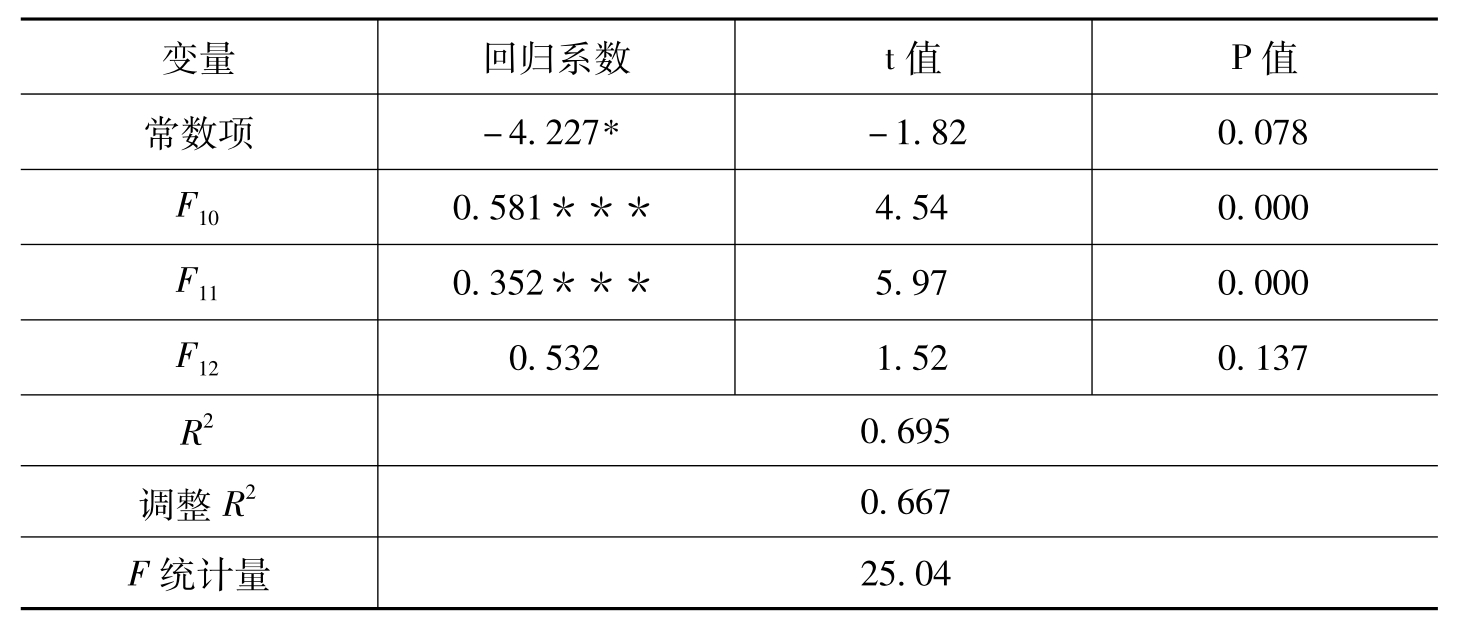
利用SPSS 15.0对全球品牌样本数据进行多元回归分析，模型4的回归系数如表6－40所示。回归模型4的R²= 0.695，调整R²= 0.667，表示回归方程拟合优度较好。F= 25.04(P＜0.01)，表明多元回归模型4通过显著性检验。由表6－40可知，模型5的F₁₀和F₁₁的回归系数在1%水平上通过显著性检验，表明F₁₀和F₁₁对全球品牌价值成长具有显著的正向影响作用; F₁₂的回归系数没有通过显著性检验，表明F₁₂对全球品牌价值成长没有显著的正向作用。

表6－40　　　　　模型4的参数估计结果

根据模型4的回归结果，市场业绩因子(F₁₀)、产品研发设计能力因子(F₁₁)对全球品牌价值成长具有显著的正向影响作用，H₄₁和H₄₂假设得到支持，而营销沟通能力因子(F₁₂)对全球品牌价值成长的影响不明显，H₄₃假设不成立，如表6－41所示。

表6－41　　　　　模型4假设检验验证结果总结

5.研究结果分析

由模型4的回归系数可知，市场业绩因子(F₁₀)、产品研发设计能力因子(F₁₁)对全球品牌价值驱动模型的贡献率分别为0.581和0.352，前者的贡献率高于后者，是第一大驱动因素，表明企业的市场业绩对全球品牌价值增值的影响程度较大，企业产品研发设计能力对全球品牌价值成长的影响作用相对较小。

三、双区域国际品牌价值驱动因素分析

1.探索性因子分析评估结果分析

利用SPSS 15.0采用主成分析法提取公共因子，分析结果如表6－42所示。其中，有2个公共因子的特征值大于1，方差累积贡献率为87.47%。为了能够较好地与全球品牌子样本的研究结果进行对比分析，将进一步进行因子旋转分析，利用最大方差正交旋转法进行因子旋转，得到旋转后因子载荷矩阵，如表6－43所示。

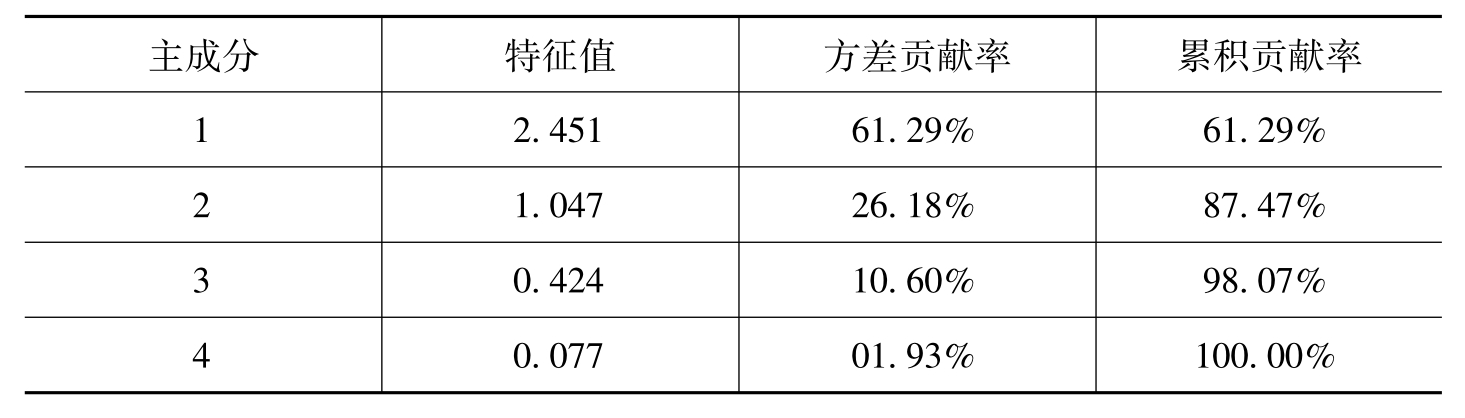
注:利用主成分分析法提取公共因子

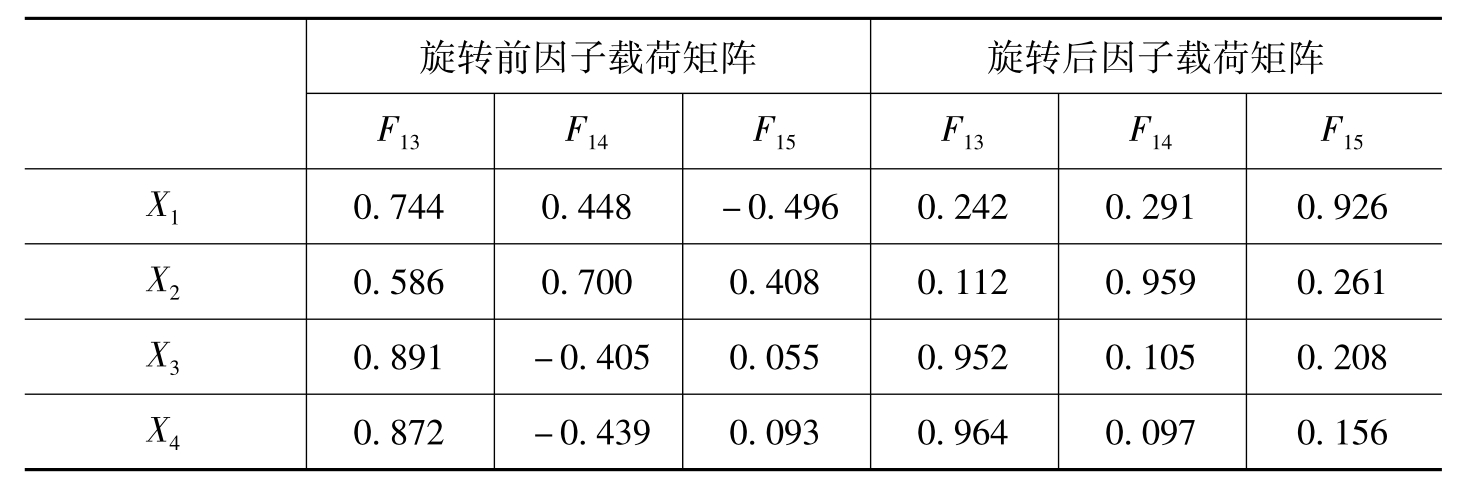
由表6－43旋转前因子载荷阵可知，直接提取三个公共因子，不能赋予三个公共因子合理的经济解释。为了解决各个公共因子的典型代表变量不很突出的问题，还将进行因子旋转分析。利用最大方差正交旋转法进行因子旋转，得到旋转后因子载荷矩阵，如表6－43所示。其中，F₁₃在X₃(营业利润)和X₄(净利润)上的载荷较大，载荷量分别为0.952和0.964，这两个变量基本上反映了双区域国际品牌为企业带来的市场业绩，将F₁₃命名为市场业绩因子; F₁₄在X₂(研发费用)上的载荷较大，载荷量为0.959，这个变量基本上反映了双区域国际品牌的产品研发设计能力，将F₁₄命名为产品研发设计能力因子; F₁₅在X₁(广告费用)上的载荷最大，载荷量为0.926，反映了双区域品牌的营销沟通能力，将F₁₅命名为营销沟通能力因子。

表6－43　　　　　双区域国际品牌样本旋转前后因子载荷矩阵

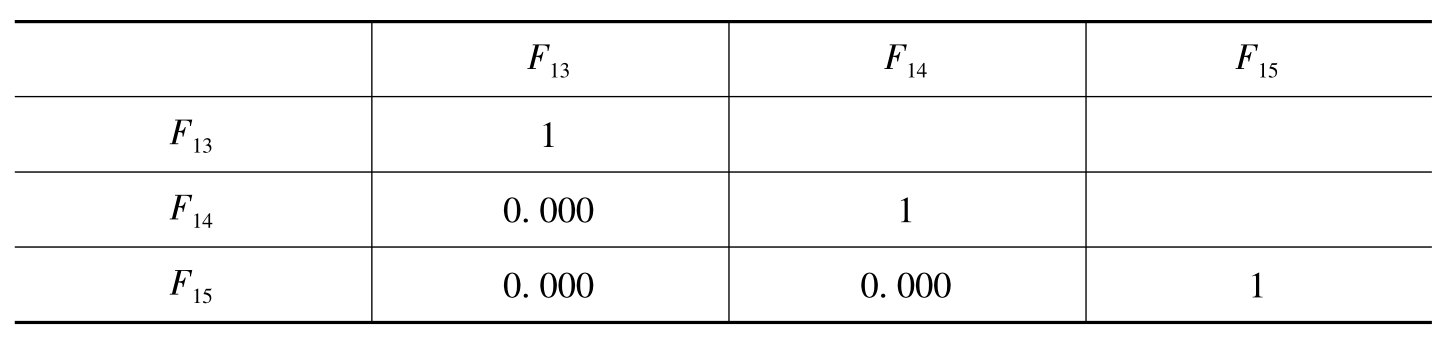
由表6－44估计回归因子分数的协方差矩阵(即三个公共因子间的相关矩阵)可知，样本数据利用最大方差正交旋转法进行因子旋转后，三个公共因子F₁₃、F₁₄和F₁₅是完全不相关的，表明旋转后得到的结果可靠。

表6－42　　　　　　双区域国际品牌的相关矩阵的特征值方差贡献率和累积贡献率

表6－44　　　　　估计回归因子分数的协方差矩阵

2.计算公共因子得分

因子分析的目的是减少变量个数，以便在进一步分析中用较少的公共因子代替原有变量进行数据建模。由于公共因子是不可观测的隐变量，需通过计算因子得分给提取的公共因子赋值。因子得分求解的过程就是以原始变量的线性组合来表示公共因子，因子得分系数是原始变量的权重。利用回归法估计因子得分，因子得分函数是:

F_j=β_j1 X₁+β_j2 X₂+…+β_jp X_p(p= 1，2，3，4，5; j= 1，2，3)上式中，β为回归法得出的因子得分系数，具体的因子得分系数如表6－45所示。

表6－45　　　　　双区域国际品牌的因子得分系数

由此可得到市场业绩因子(F₁₃)、产品研发设计能力因子(F₁₄)、营销沟通能力因子(F₁₅)三个公共因子得分的计算公式为:

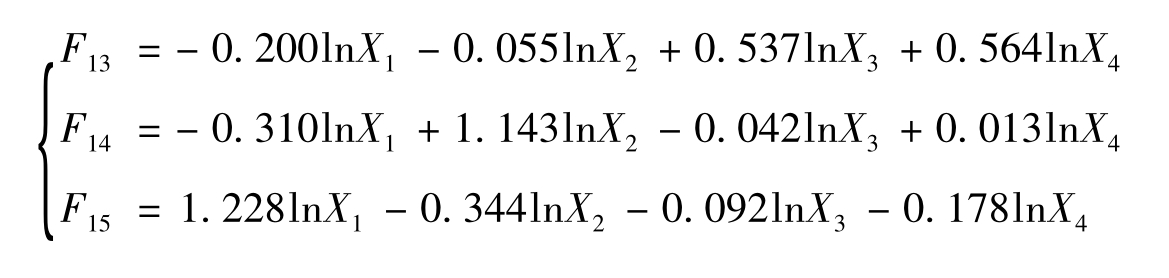
(公式5)

这三个公共因子是否是双区域国际品牌价值的驱动因素，对其品牌价值成长的影响程度是多少，需要进一步进行回归分析予以验证。

3.研究假设

根据探索性因子分析结果，双区域国际品牌价值的驱动因素包括三个方面:企业的市场业绩、产品研发设计能力和营销沟通能力。这三个驱动因素是否对双区域国际品牌价值的成长具有显著影响，需要进一步进行深入分析。因此，提出如下假设:

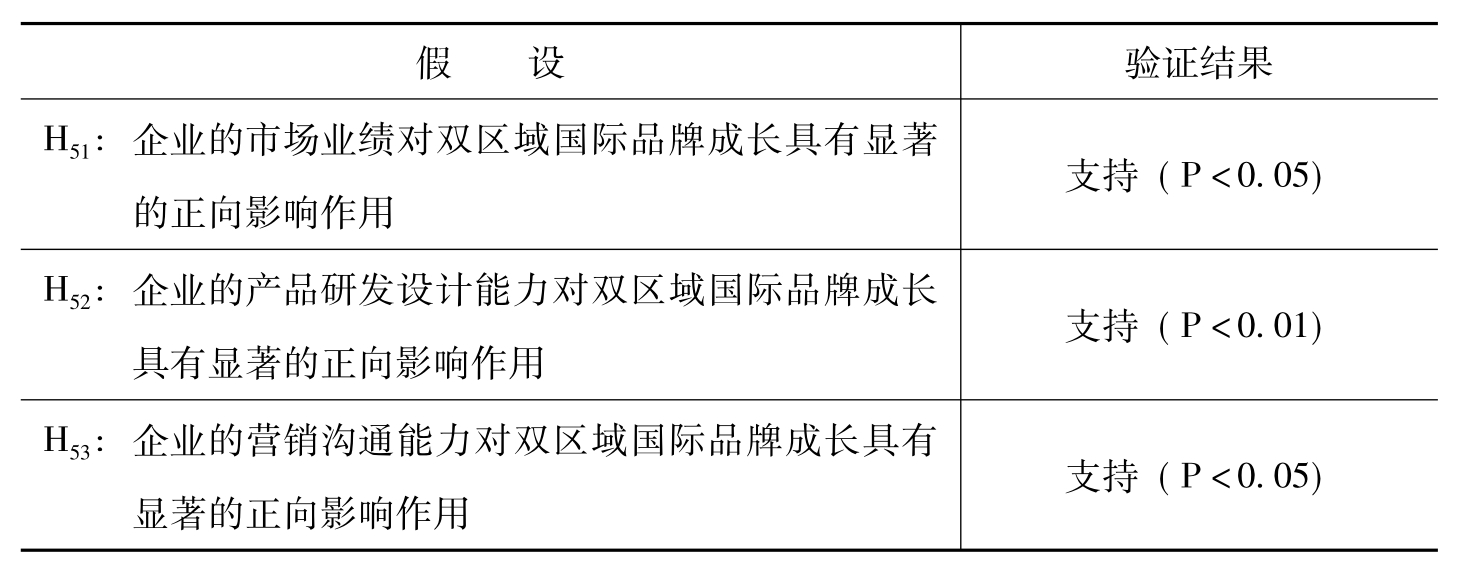
H₅₁:企业的市场业绩对双区域国际品牌成长具有显著的正向影响作用。

H₅₂:企业的产品研发设计能力对双区域国际品牌成长具有显著的正向影响作用。

H₅₃:企业的营销沟通能力对双区域国际品牌成长具有显著的正向影响作用。

根据上述提出的研究假设，建立多元回归方程，如下所示:

ln Y₅=β₅₀+β₅₁ F₁₃+β₅₂ F₁₄+β₅₃ F₁₅+ε₅(模型5)

Y₅表示双区域国际品牌价值; F₁₃表示市场业绩驱动因子;

F₁₄表示产品研发设计能力驱动因子;

F₁₅表示营销沟通能力驱动因子。

4.实证分析过程

由于F₁₃、F₁₄和F₁₅是通过探索性因子分析得到的公共因子，不能直接获得观测值，因此，它们的取值利用公式5计算得到，即因子得分。双区域国际品牌价值(Y₅)的数据来自2001—2008年Interbrand“全球品牌100强”发布的双区域国际品牌价值。F₁₃、F₁₄和F₁₅的取值是利用自变量观测值的对数值根据公式5计算得到。为了保证处理数据的一致性，将因变量的取值也取对数。

利用SPSS 15.0对多元回归模型的变量进行相关分析，计算各个变量之间的皮尔森相关系数，检验各个变量之间的相关关系。如表6－46所示，自变量F₁₃、F₁₄和F₁₅与Y₅有显著正相关关系。由表6－44估计回归因子分数的协方差矩阵可知，三个自变量之间是完全不相关的，因此，自变量之间不会存在多重共线性的问题，可以直接进行多元回归分析。

表6－46　　　　　双区域国际品牌样本各变量的皮尔森相关系数矩阵和描述性统计分析

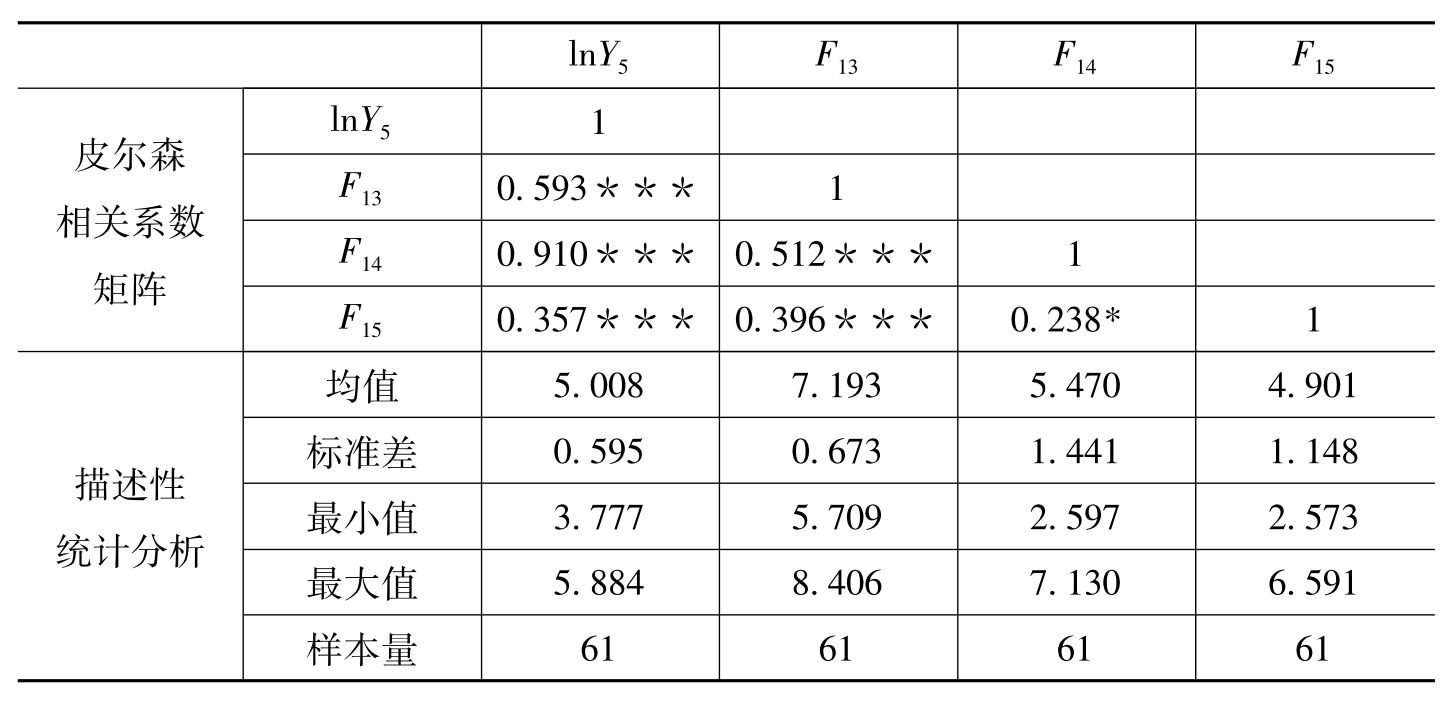
注:＊＊＊表示在1%水平上显著，＊＊表示在5%水平上显著，*表示在10%水平上显著

利用SPSS 15.0对双区域国际品牌样本数据进行多元回归分析，模型5的回归系数如表6－47所示。回归模型5的R²= 0.861，调整R²= 0.853，表明模型5的拟合优度较好。F= 113.49(P＜0.01)，表明多元回归模型5通过显著性检验。由表6－47可知，模型5的回归系数F₁₃和F₁₅均在5%水平上通过显著性检验，F₁₄在1%水平上通过显著性检验，表明F₁₃、F₁₄和F₁₅都对Y₅具有显著的正向影响作用。

表6－47　　　　　模型5的参数估计结果

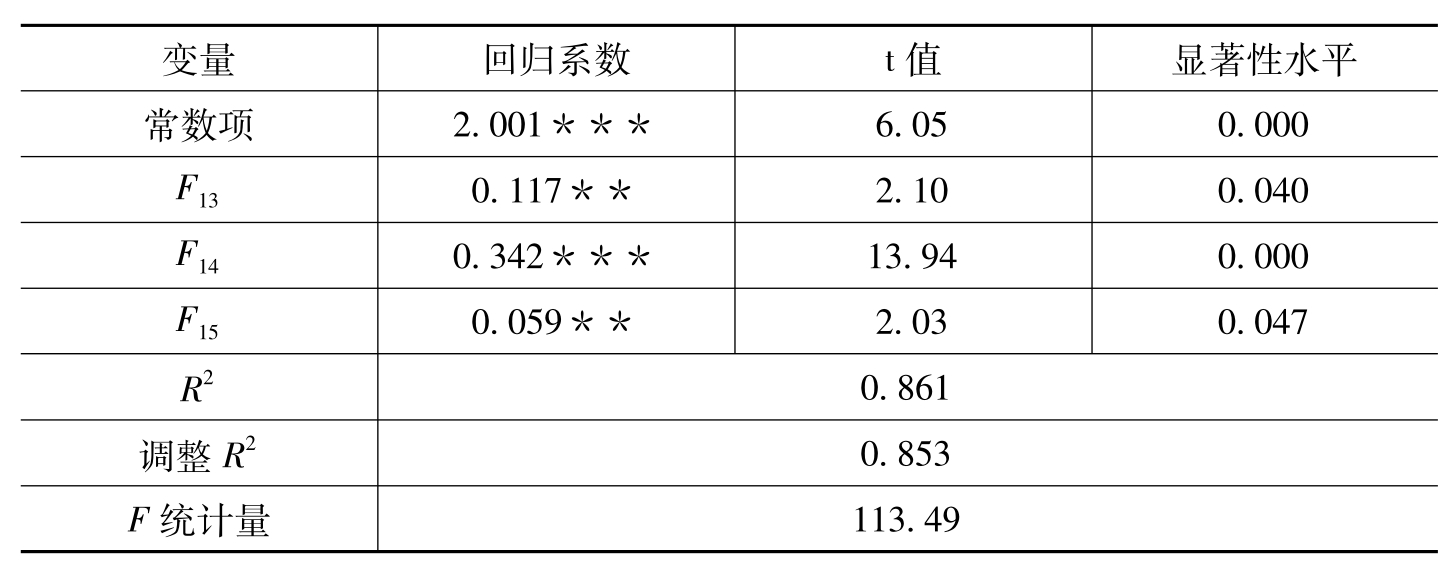
注:＊＊＊表示在1%水平上显著，＊＊表示在5%水平上显著，*表示在10%水平上显著

根据模型5的回归结果，市场业绩因子(F₁₃)、产品研发设计能力因子(F₁₄)、营销沟通能力因子(F₁₅)都对双区域国际品牌成长具有显著的正向影响作用，H₅₁、H₅₂、H₅₃都得到支持，如表6－48所示。

表6－48　　　　　模型5假设检验验证结果总结

5.研究结果分析

由模型5的回归系数可知，市场业绩因子(F₁₃)、产品研发设计能力因子(F₁₄)、营销沟通能力因子(F₁₅)对双区域国际品牌价值驱动模型的贡献率分别为0.117、0.342和0.059，市场业绩因子对双区域国际品牌成长的影响作用相对较大，另外两个驱动因子对双区域国际品牌成长的影响作用相对较小。

四、区域国际品牌价值驱动因素分析

1.探索性因子分析评估结果分析

利用SPSS 15.0采用主成分分析法提取公共因子，分析结果如表6－49所示。其中，只有1个公共因子的特征值大于1，方差累积贡献率为70.88%，没有达到公共因子累计方差超过85%的标准。因此，将进一步进行因子旋转分析，利用最大方差正交旋转法进行因子旋转，得到旋转后因子载荷矩阵，如表6－50所示。

表6－49　　　　　区域国际品牌的相关矩阵的特征值、方差贡献率和累积贡献率

续表

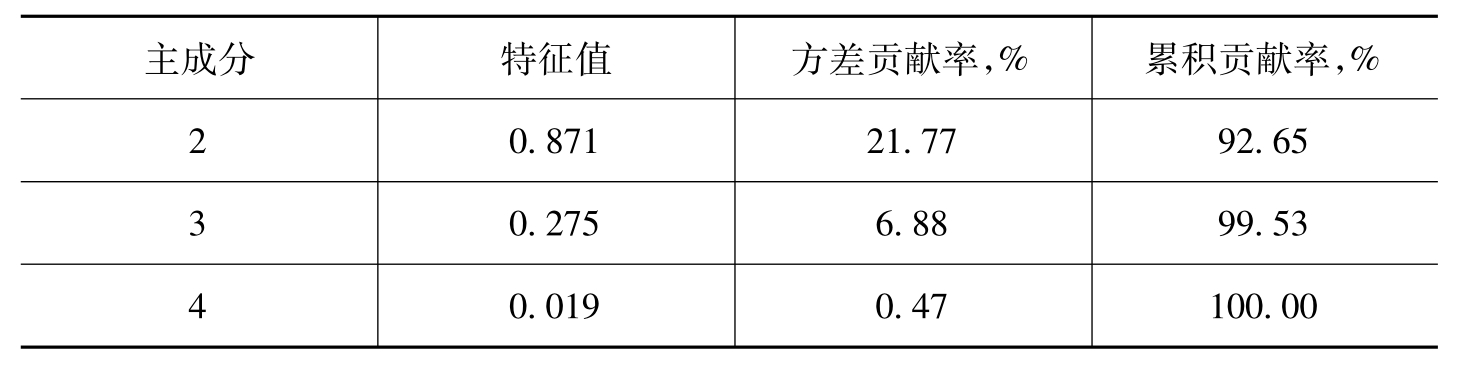
注:利用主成分分析法提取公共因子

由表6－50旋转前因子载荷阵可知，直接提取三个公共因子，不能赋予三个公共因子合理的经济解释。为了解决各个公共因子的典型代表变量不很突出的问题，还将进行因子旋转分析。利用最大方差正交旋转法进行因子旋转，得到旋转后因子载荷矩阵，如表6－50所示。其中，F₁₆在X₃(营业利润)和X₄(净利润)上的载荷较大，载荷量分别为0.940和0.958，这两个变量基本上反映了区域国际品牌为企业带来的市场业绩，将F₁₆命名为市场业绩因子; F₁₇在X₁(广告费用)上的载荷最大，载荷量为0.953，反映了区域国际品牌的营销沟通能力，将F₁₇命名为营销沟通能力因子; F₁₈在X₂(研发费用)上的载荷较大，载荷量为0.841，这个变量基本上反映了区域国际品牌的产品研发设计能力，将F₁₈命名为产品研发设计能力因子。

表6－50　　　　　区域国际品牌样本旋转前后因子载荷矩阵

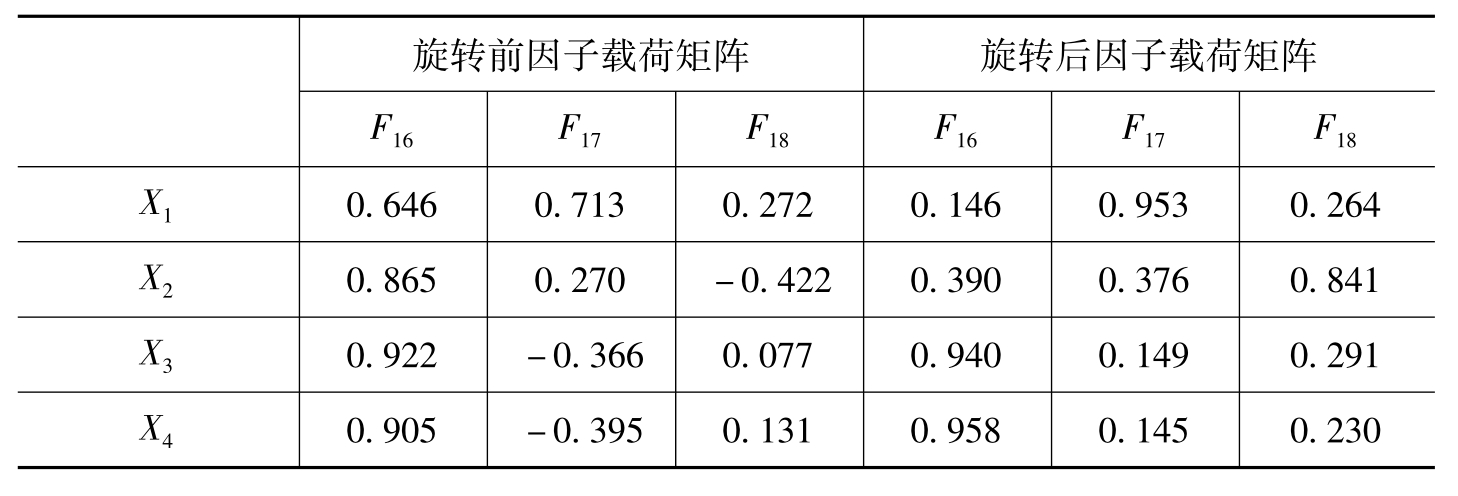
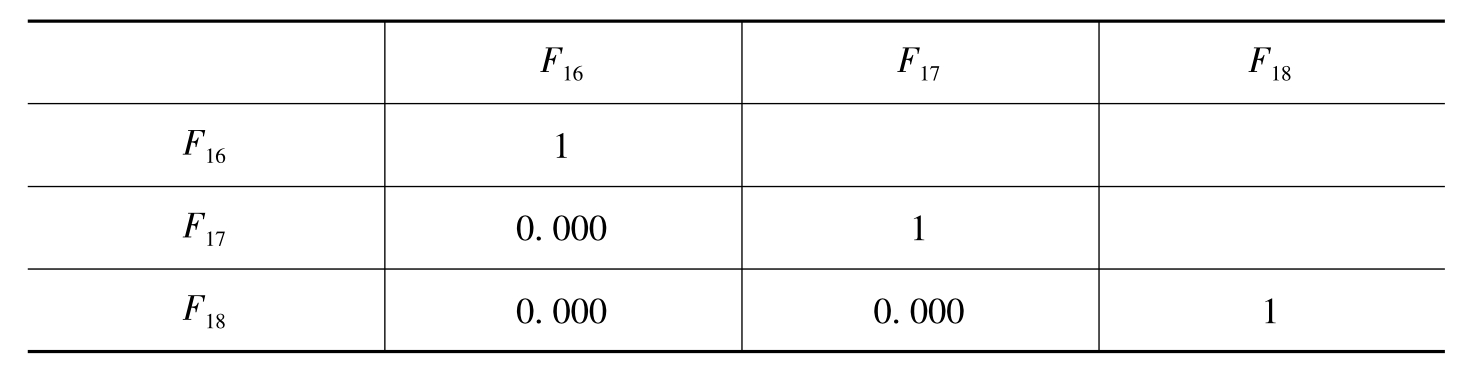
由表6－51估计回归因子分数的协方差矩阵(即三个公共因子间的相关矩阵)可知，样本数据利用最大方差正交旋转法进行因子旋转后，三个公共因子F₁₆、F₁₇和F₁₈是完全不相关的，表明旋转后得到的结果可靠。

表6－51　　　　　估计回归因子分数的协方差矩阵

2.计算公共因子得分

因子分析的目的是减少变量个数，以便在进一步分析中用较少的公共因子代替原有变量进行数据建模。由于公共因子是不可观测的隐变量，需通过计算因子得分给提取的公共因子赋值。因子得分求解的过程就是以原始变量的线性组合来表示公共因子，因子得分系数是原始变量的权重。利用回归法估计因子得分，因子得分函数是:

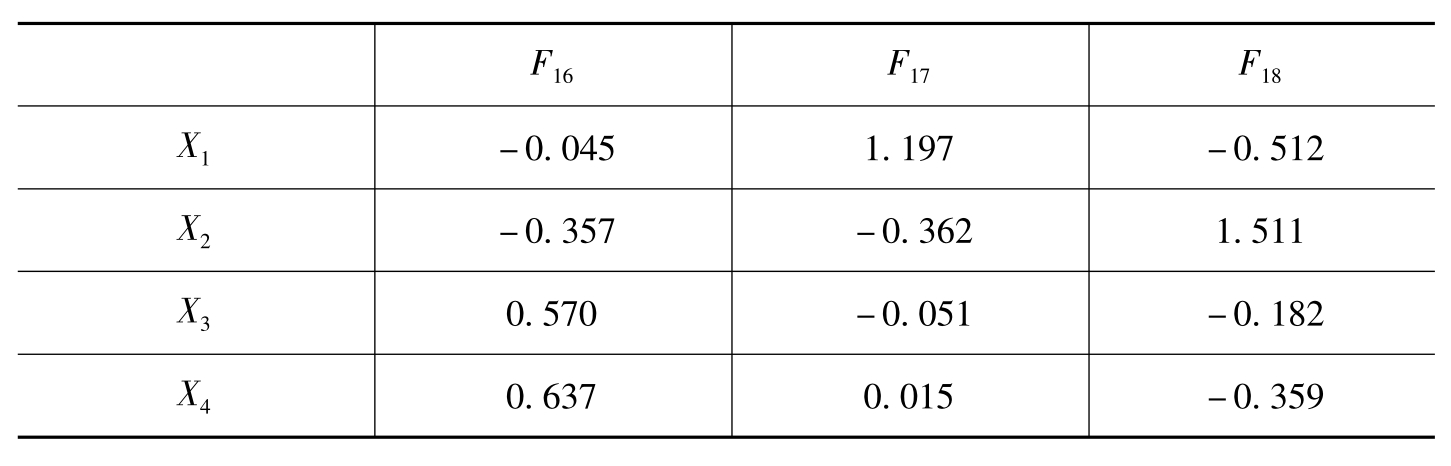
F_j=β_j1 X₁+β_j2 X₂+…+β_jp X_p(p= 1，2，3，4，5; j= 1，2，3)上式中，β为回归法得出的因子得分系数，具体的因子得分系数如表6－52所示。

表6－52　　　　　区域国际品牌的因子得分系数

由此可得到市场业绩因子(F₁₆)、营销沟通能力因子(F₁₇)和产品研发设计能力因子(F₁₈)三个公共因子得分的计算公式为:

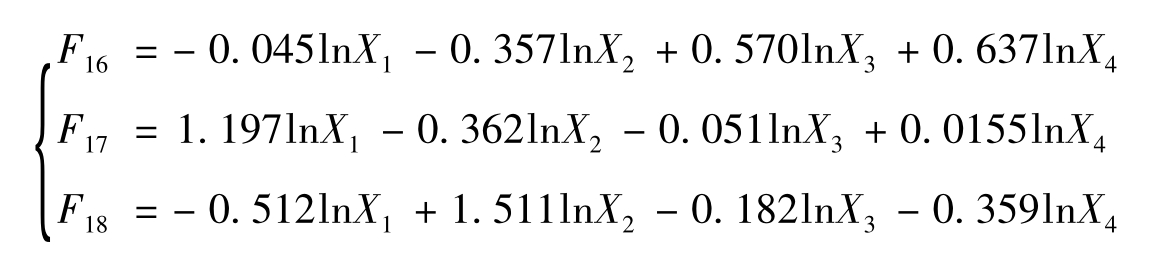
(公式6)

这三个公共因子是否是区域国际品牌价值的驱动因素，对其品牌价值成长的影响程度是多少，需要进一步进行回归分析予以验证。

3.研究假设

根据探索性因子分析结果，区域国际品牌成长的驱动因素包括三个方面:市场业绩、营销沟通能力和产品研发设计能力。这三个驱动因素是否对区域国际品牌价值的成长具有显著影响，需要进一步进行深入分析。因此，提出如下假设:

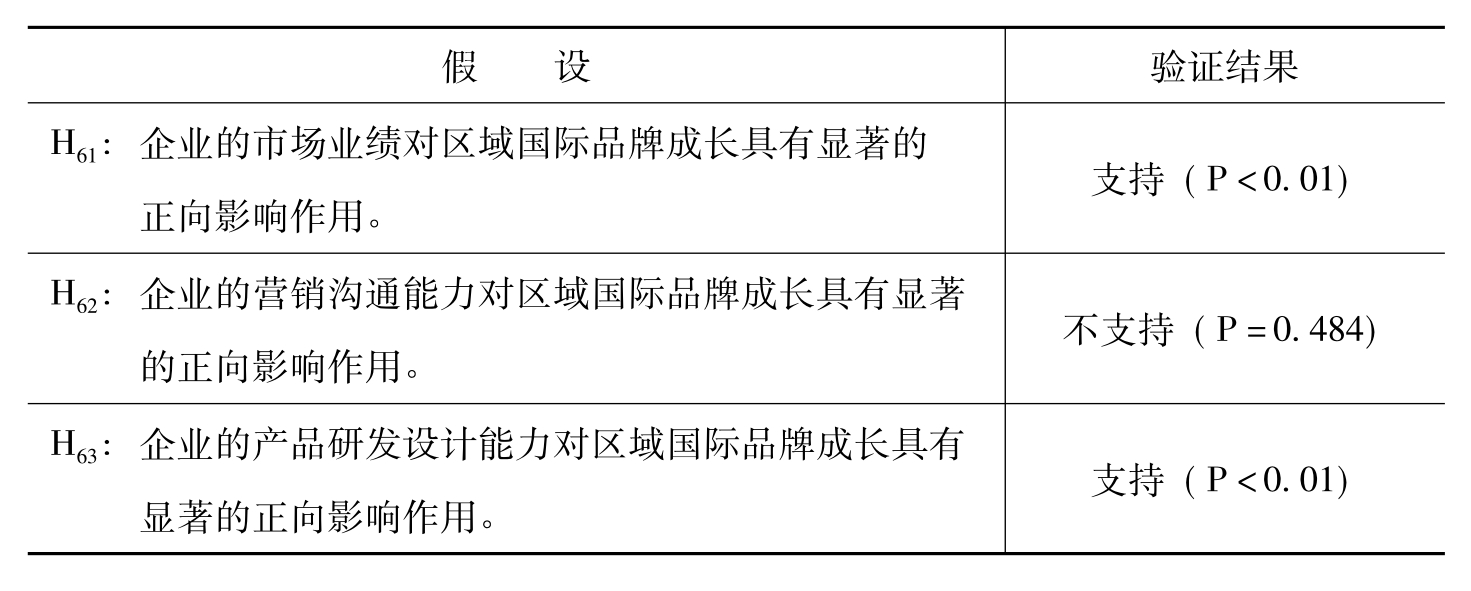
H₆₁:企业的市场业绩对区域国际品牌成长具有显著的正向影响作用。

H₆₂:企业的营销沟通能力对区域国际品牌成长具有显著的正向影响作用。

H₆₃:企业的产品研发设计能力对区域国际品牌成长具有显著的正向影响作用。

根据上述提出的研究假设，建立多元回归方程，如下所示:

ln Y₆=β₆₀+β₆₁ F₁₆+β₆₂ F₁₇+β₆₃ F₁₈+ε₆(模型6)

Y₆表示区域国际品牌价值; F₁₆表示市场业绩驱动因子;

F₁₇表示营销沟通能力驱动因子;

F₁₈表示产品研发设计能力驱动因子。

4.实证分析过程

由于F₁₆、F₁₇和F₁₈是通过探索性因子分析得到的公共因子，不能直接获得观测值，因此，它们的取值利用公式6计算得到，即因子得分。国际品牌价值(Y₆)的数据来自2001—2008年Interbrand“全球品牌100强”发布的区域国际品牌价值。F₁₆、F₁₇和F₁₈的取值是利用自变量观测值的对数值根据公式6计算得到。为了保证处理数据的一致性，将因变量的取值也取对数。

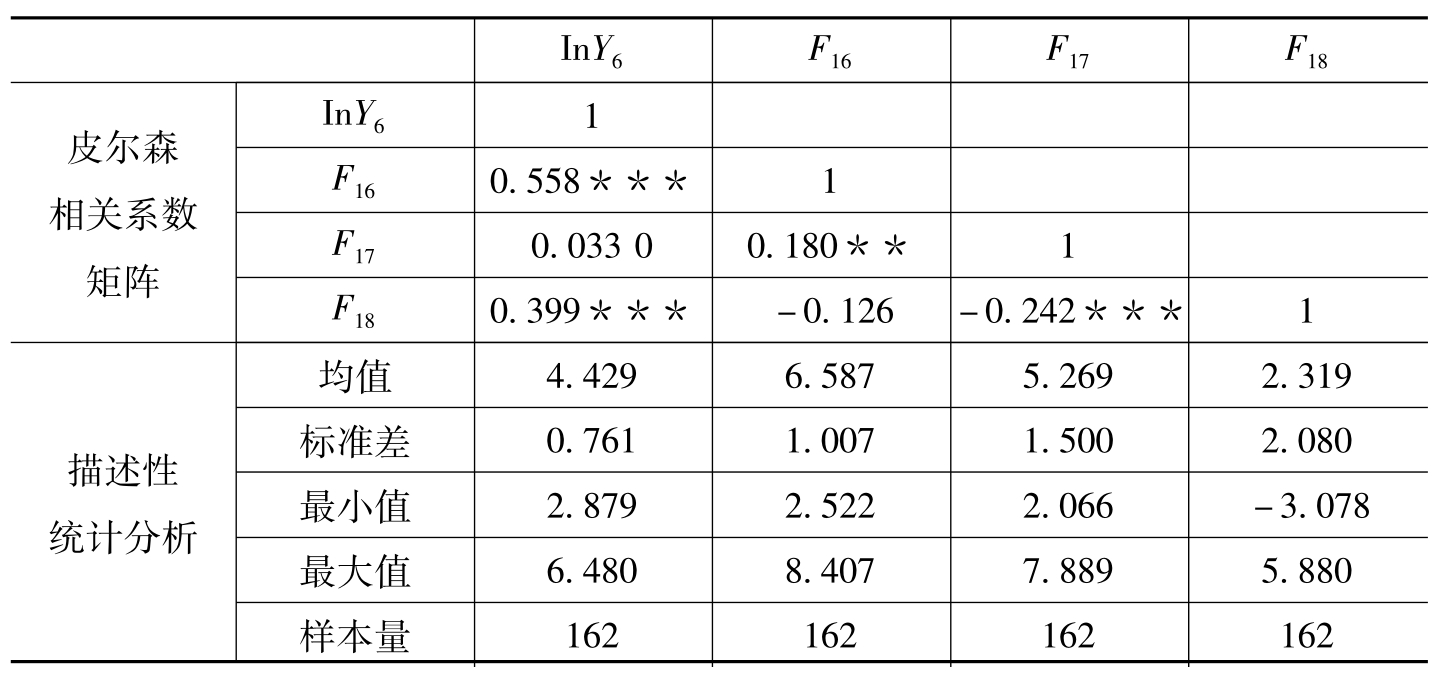
利用SPSS 15.0对多元回归模型的变量进行相关分析，计算各个变量之间的皮尔森相关系数，如表6－53所示，自变量F₁₆、F₁₈与Y₆有显著正相关关系，自变量F₁₇与Y₆没有显著相关关系。由表6－51估计回归因子分数的协方差矩阵可知，三个自变量之间是完全不相关的，因此，自变量之间不会存在多重共线性的问题，可以直接进行多元回归分析。

注:＊＊＊表示在1%水平上显著，＊＊表示在5%水平上显著，*表示在10%水平上显著

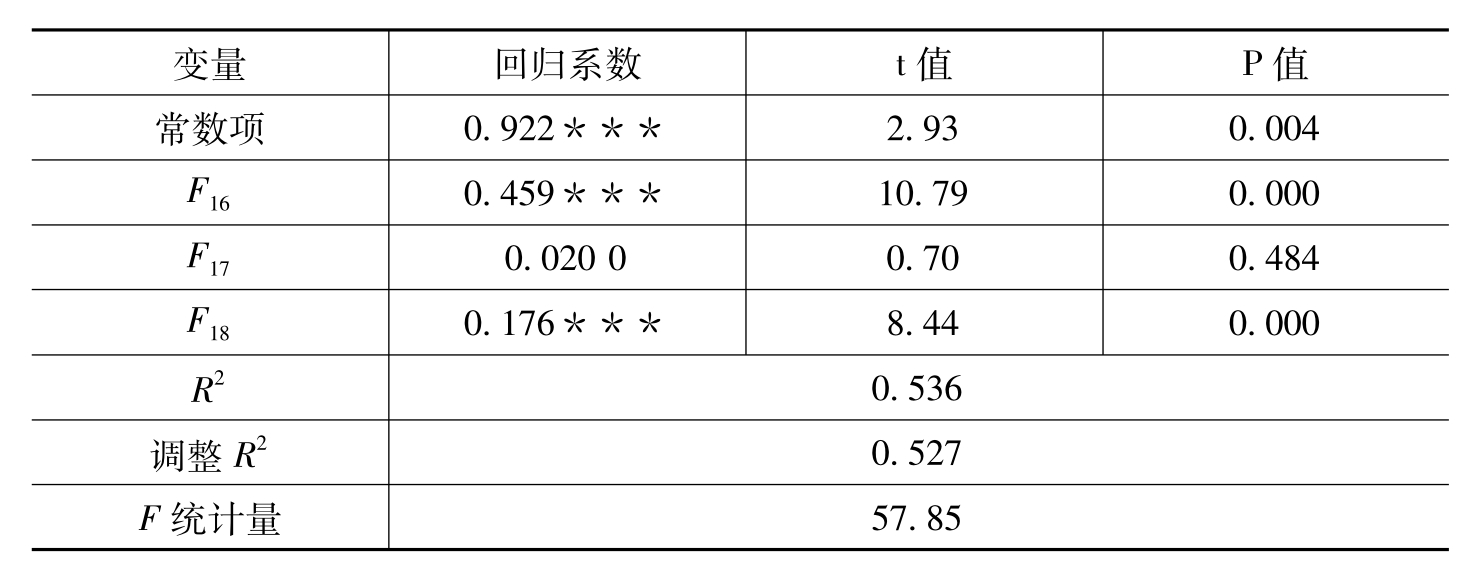
利用SPSS 15.0对区域国际品牌样本数据进行多元回归分析，模型6的回归系数如表6－54所示。回归模型6的R²= 0.536，调整R²= 0.527，表明模型6的拟合优度较好。F= 57.85(P＜0.01)，表明多元回归模型6通过显著性检验。由表6－54可知，模型6的F₁₆和F₁₈的回归系数均在1%水平上通过显著性检验，表明F₁₆和F₁₈对区域国际品牌成长具有显著的正向影响作用; F₁₇的回归系数没有通过显著性检验，表明F₁₇对区域国际品牌成长不具有显著影响。

表6－54　　　　　模型6的参数估计结果

注:＊＊＊表示在1%水平上显著，＊＊表示在5%水平上显著，*表示在10%水平上显著

表6－53　　　　　区域国际品牌样本各变量的皮尔森相关系数矩阵和描述性统计分析

根据模型6的回归结果，市场业绩因子(F₁₆)、产品研发设计能力因子(F₁₈)对区域国际品牌成长具有显著的正向影响作用，H₆₁和H₆₃假设得到支持，而营销沟通能力因子(F₁₇)对区域国际品牌成长的影响不明显，H₆₂假设不成立，如表6－55所示。

表6－55　　　　　模型6假设检验验证结果总结

5.研究结果分析

由模型6的回归系数可知，市场业绩因子(F₁₆)对区域国际品牌成长的贡献率为0.459，远远高于另外一个驱动因子的贡献率，是第一大驱动因素，表明企业的市场业绩对区域国际品牌价值增值的影响程度较大;产品研发设计能力因子(F₁₈)对区域国际品牌价值驱动模型的贡献率为0.176，表明企业产品研发设计能力对区域国际品牌价值增值的影响程度较小;营销沟通能力因子(F₁₇)对区域国际品牌成长没有显著影响作用。

五、小结

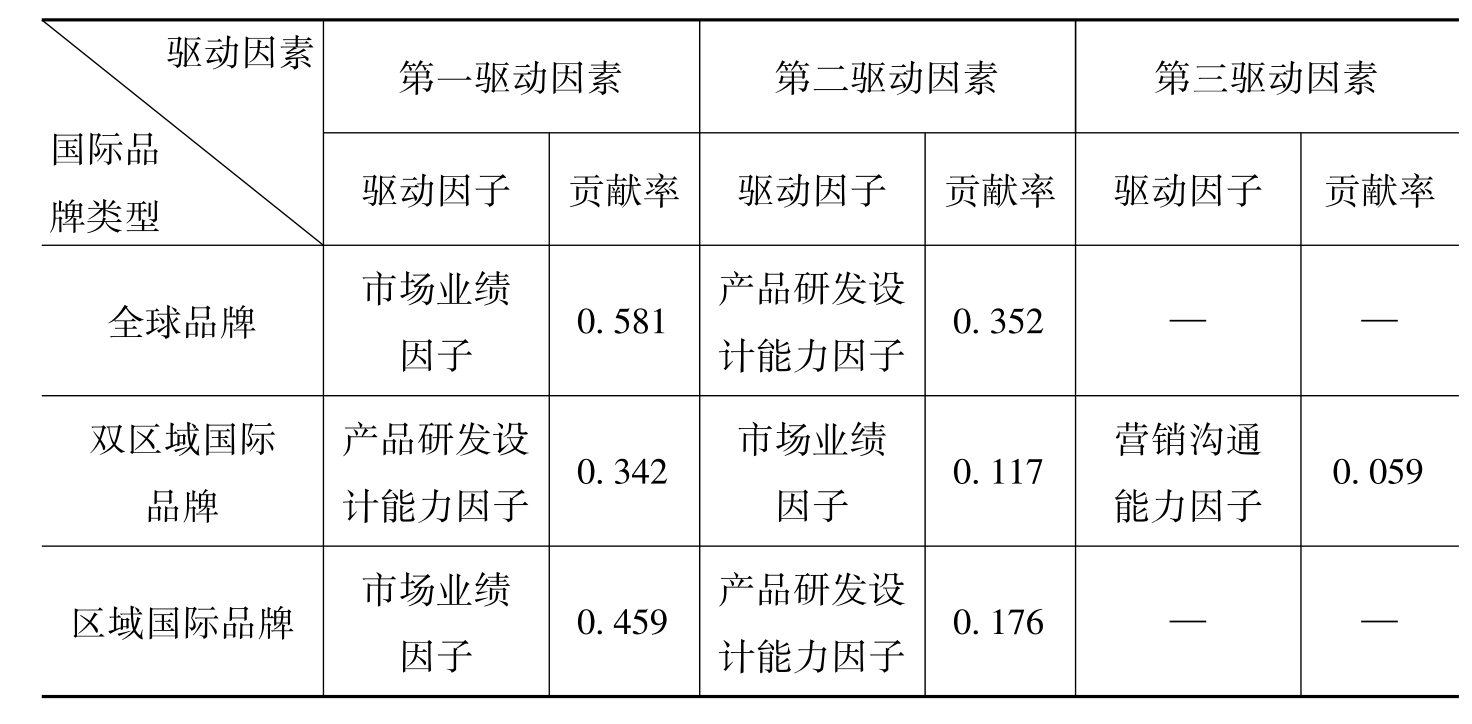
由不同类型国际品牌价值驱动因素分析结果可知，全球品牌、双区域国际品牌和区域国际品牌价值驱动因素存在着差异，如表6－56所示:①双区域国际品牌与全球品牌和区域国际品牌的驱动因素不同，它有3个驱动因子，包括市场业绩因子、产品研发设计因子和营销沟通能力因子;而全球品牌和区域国际品牌成长驱动因子都只有2个，分别是市场业绩因子和产品研发设计因子。②三类国际品牌的第一大驱动因子也各不相同，双区域国际品牌的第一驱动因子是产品研发设计能力因子，而全球品牌和区域国际品牌的第一大驱动因子都是市场业绩因子。

表6－56　　　　　不同类型国际品牌价值驱动因素及其贡献分析