第三节 误差修正模型
一、误差修正模型(ECM)
前面所讲的传统经济模型描述了经济变量之间的长期均衡关系,但是在现实经济生活中,变量之间的关系很少处在均衡点上,它们之间通常是短期的或非均衡的关系。
长期均衡模型为:y*t=α0+α1x*t+ut,其中α1为变量y关于变量x的长期弹性。
假如有如下分布滞后形式:
yt=β0+β1xt+β2xt-1+δyt-1+ut
可以得出:
Δyt=β1Δxt-λ(yt-1-α0-α1xt-1)+ut
其中,λ=1-δ,α0=β0/(1-δ),α1=(β1+β2)/(1-δ)
于是上式可以表示为:
Δyt=β1Δxt-λ·ecmt-1+ut,0<λ<1,其中β1为变量y关于变量x的短期弹性。
其中的ecm就是我们所说的误差修正项。如果yt-1>α0+α1xt-1,则有ecmt-1>0,使得Δyt减少;反之亦然。
二、ECM模型的建立
1.Granger表述定理
如果变量x与y之间存在协整关系,那么它们之间的短期非均衡关系总能有一个误差修正模型表示,即
Δyt=lagged(Δy,Δx)-λ·ecmt-1+ut,0<λ<1。
2.ECM模型的估计
方法一:EG两步法
①进行协整分析,估计协整回归向量。
②用协整回归向量的长期均衡关系参数来构建误差修正项,加入到误差修正模型,然后用OLS法估计参数。
方法二:直接估计法
在对变量之间的协整关系进行检验之后,打开误差修正模型中非均衡误差项括号,直接对下面所列的式子进行OLS法估计。
Δyt=λα0+β1Δxt-λyt-1+λα1xt-1+ut
当然我们注意到不同方法得出的结果一般都不一样。
3.例子
本章第二节中我们已经分析了中国人均居民消费(CONSP)与人均GDP之间存在协整关系,下面试图建立它们的ECM模型。
①在命令窗口中输入“genr lnc=log(consp)”,点回车键,生成时间序列{conspt}的自然对数序列{ln ct}。同理输入“genr lng=log(gdp)”,生成时间序列{gdpt}的自然对数序列{ln gt}。对原序列取自然对数后不会改变变量之间的统计性质,同时得到较平稳的序列。经过上述处理后,我们得到序列{ln ct}和{ln gt},如图10-11所示。
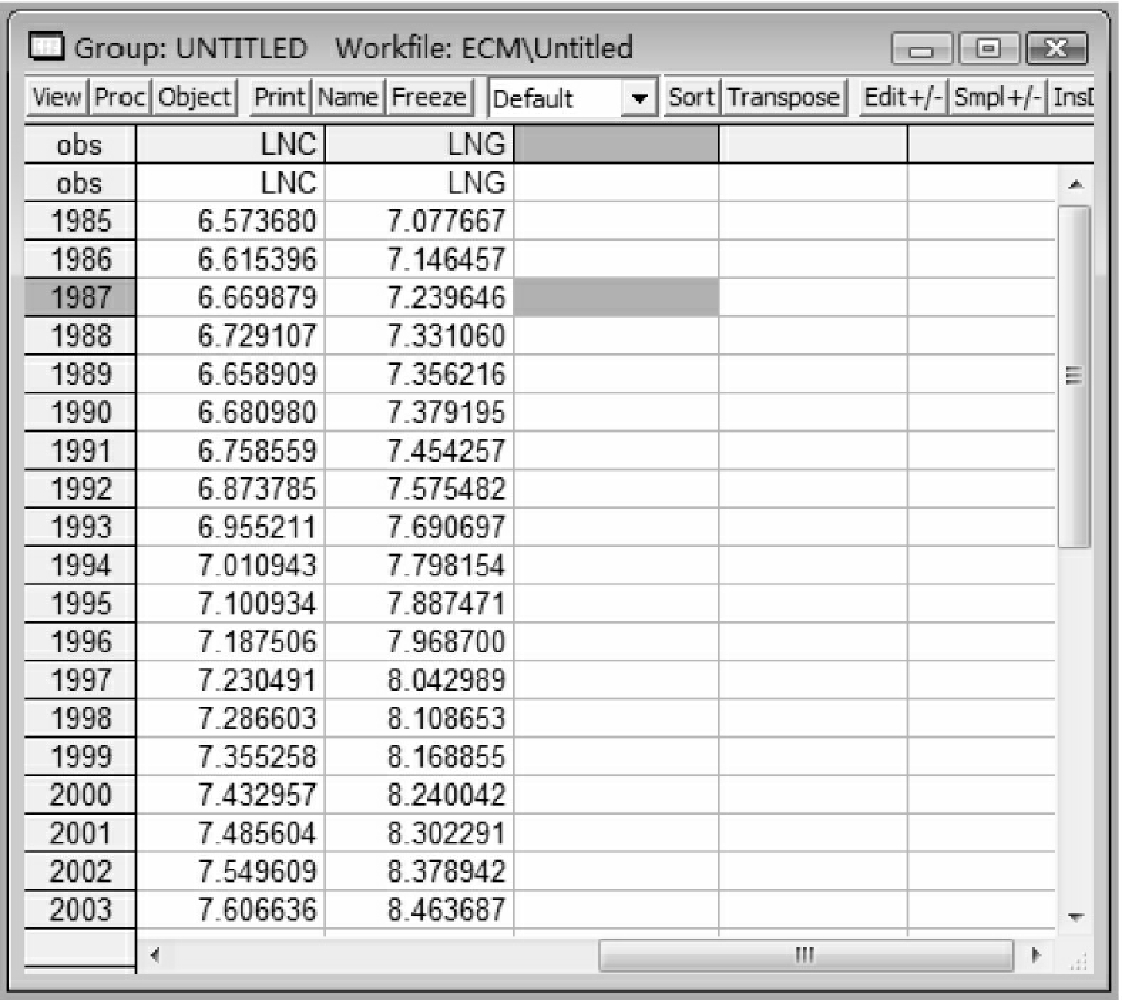
图10-11
②根据EG检验第一步,要对序列{ln ct}和{ln gt}的单整性进行分析。按照前面进行协整分析的知识,分别对这两个序列进行单位根ADF检验,检验结果如图10-12和图10-13所示,因此观察t统计量或者p值,可以认为在10%的显著水平上这两个序列都是一阶单整的时间序列,它们之间可能存在协整关系。
③以ln ct为被解释变量,ln gt为解释变量进行协整回归:点击Quick,选择Equation Estimation,如图10-14所示,输入“lnc lng”,表示回归方程中不含截距项。
④协整回归结果如图10-15所示,于是有:
ln ct=0.906ln gt
(437.56)R2=0.9592D.W=0.164
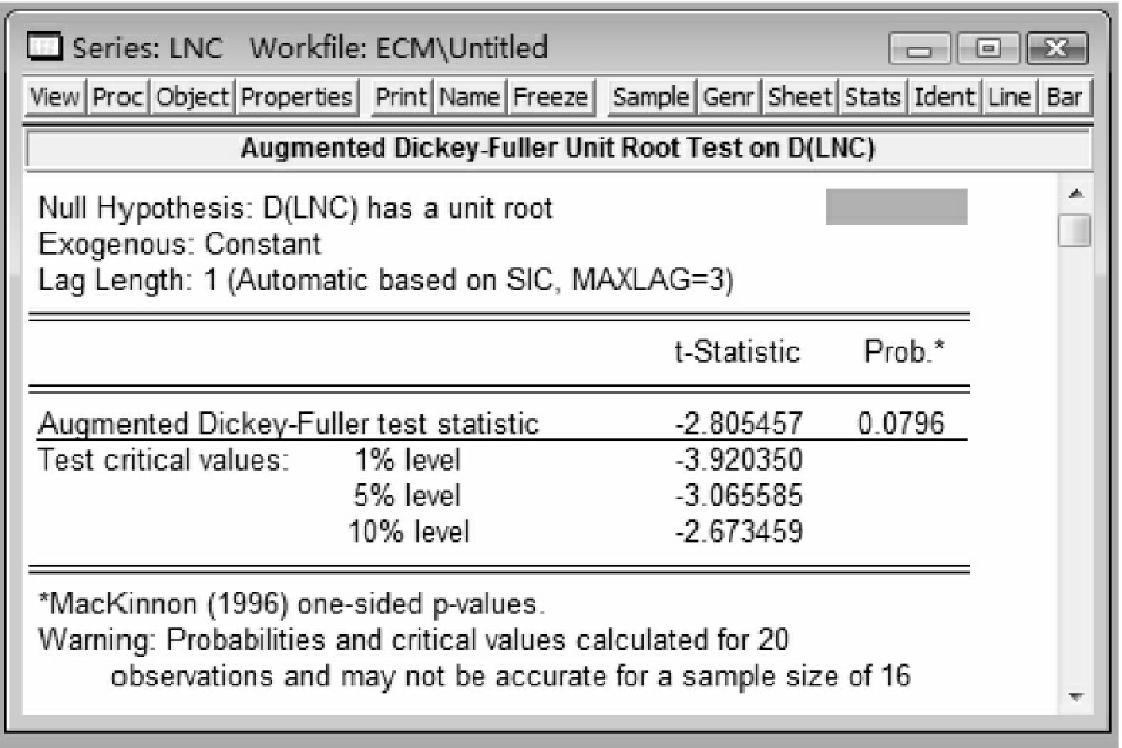
图10-12
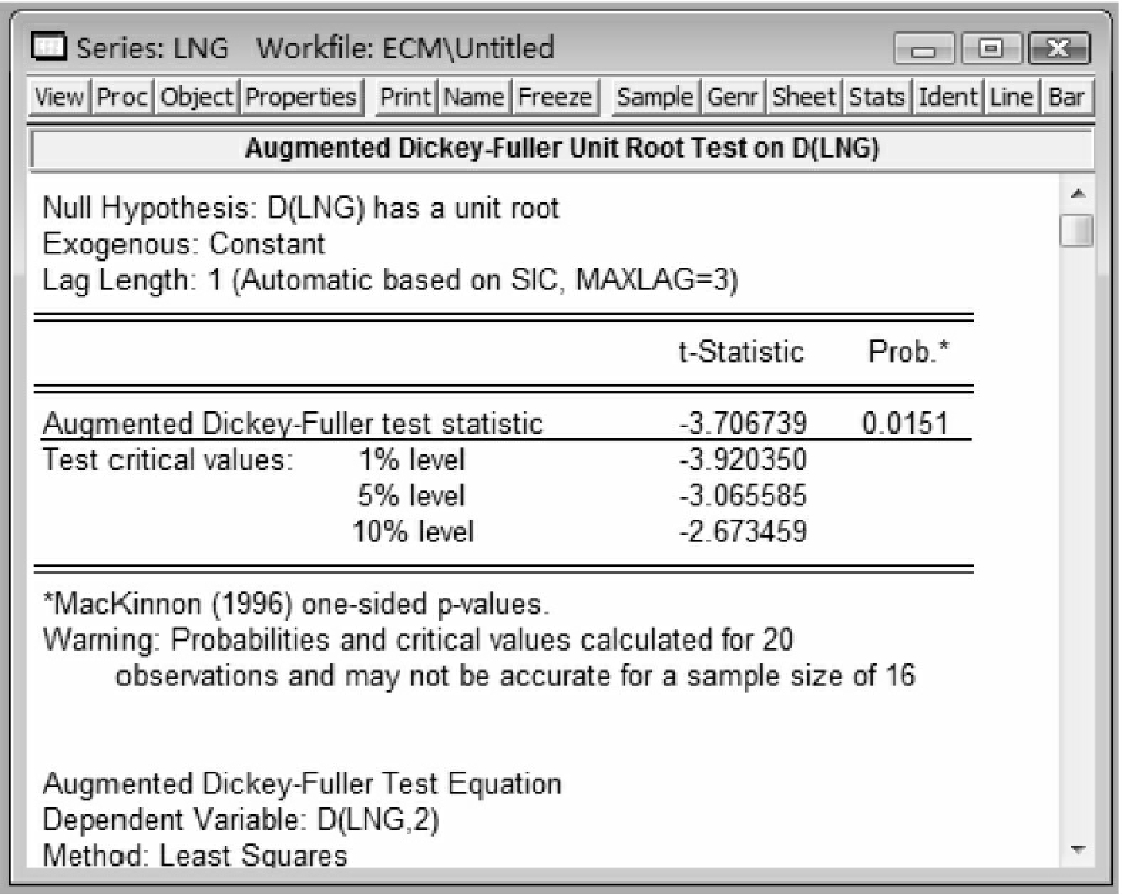
图10-13
无论从模型系数的显著性,还是从判定系数来看,这个模型都是拟合得非常好的,但是这种关系是否成立,换句话说,是否出现了伪回归现象,这需要进行进一步检验。如图10-15所示。
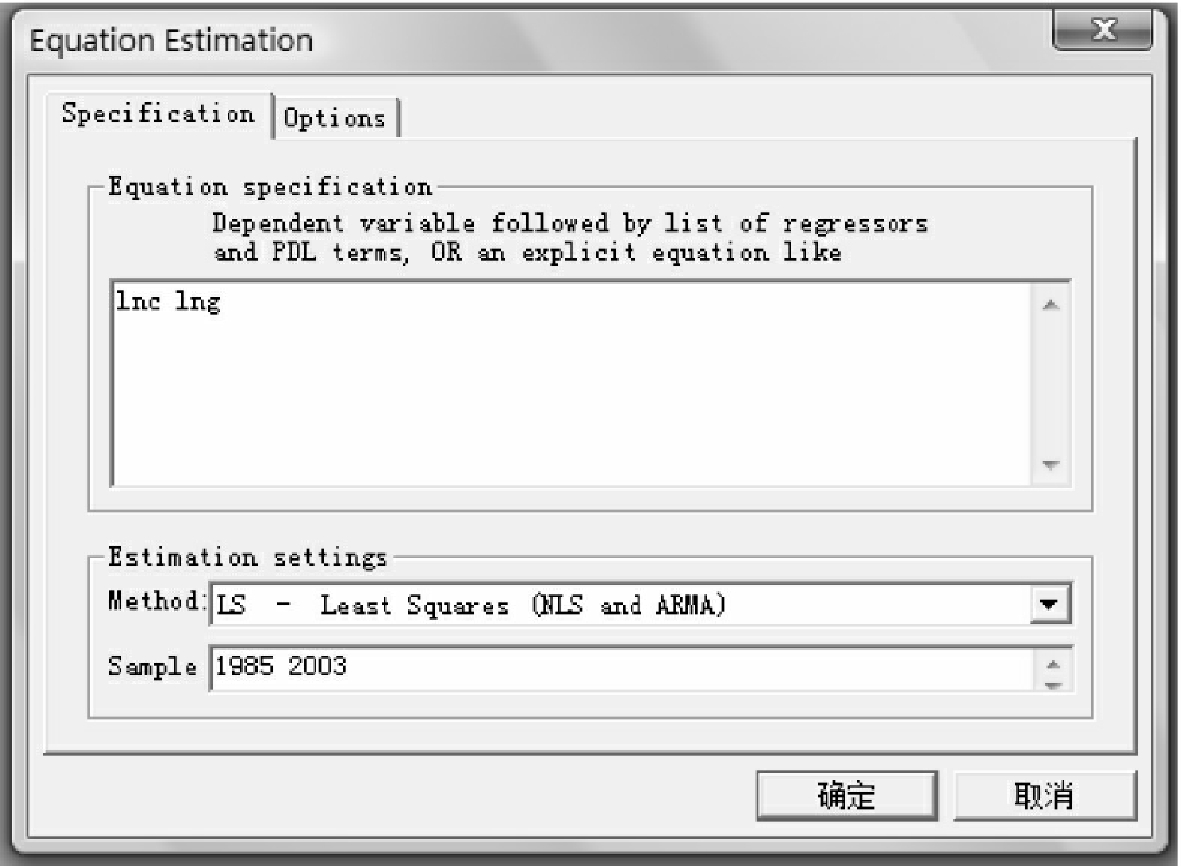
图10-14
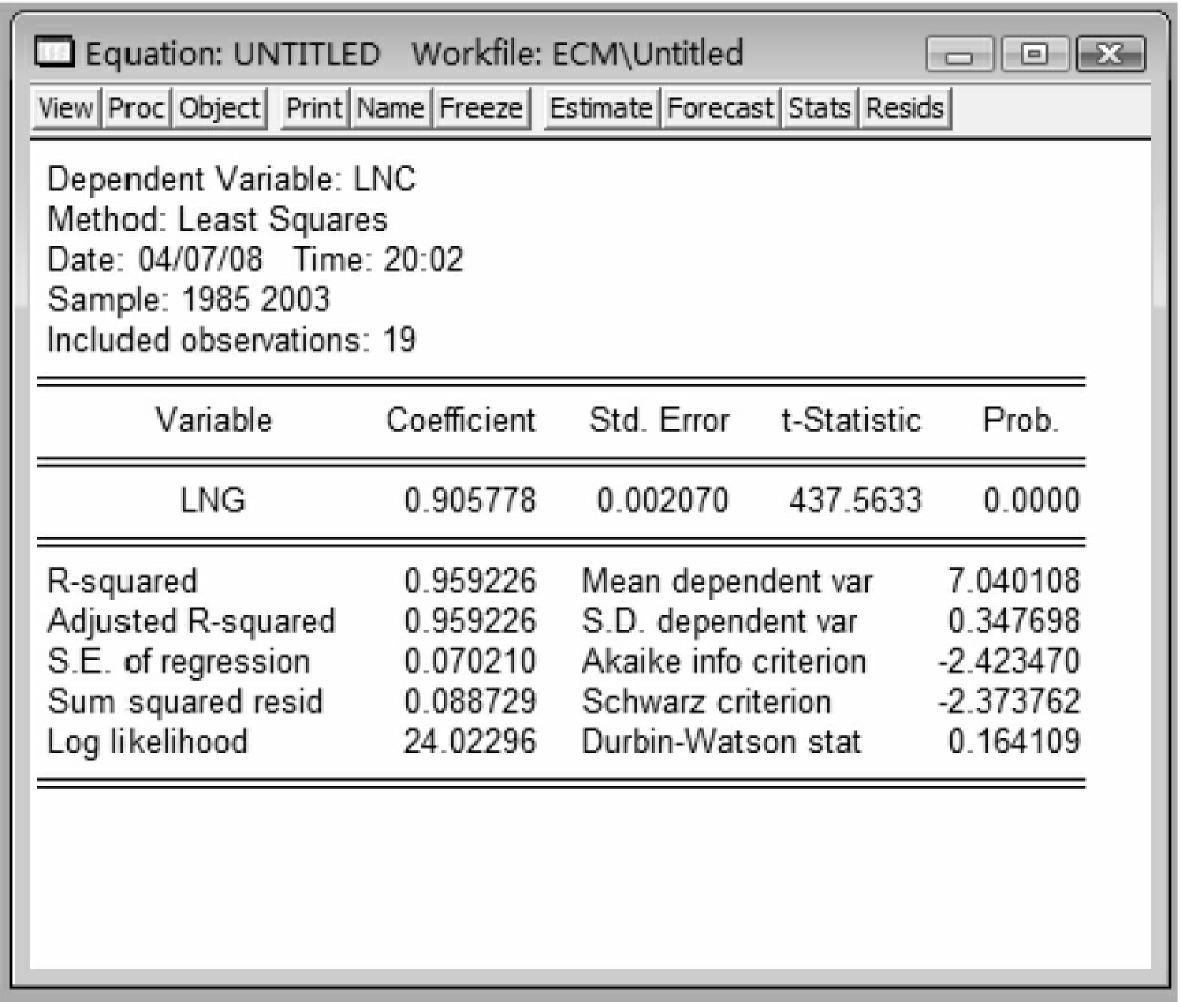
图10-15
⑤在命令窗口输入genr u=resid,使得时间序列{ut}等于残差序列。为了说明序列{ln ct}和{ln gt}之间的协整性,需要判定序列{ut}的单整阶数。同样,对序列{ut}进行单位根ADF检验的输出结果如图10-16所示,说明序列{ut}是平稳的时间序列,或者说是零阶单整的,因此序列{ln ct}和{ln gt}之间是(1,1)阶协整的。上面的协整回归模型就是变量lnCONSPt和lnGDPt的长期稳定均衡关系,长期弹性为0.9058。
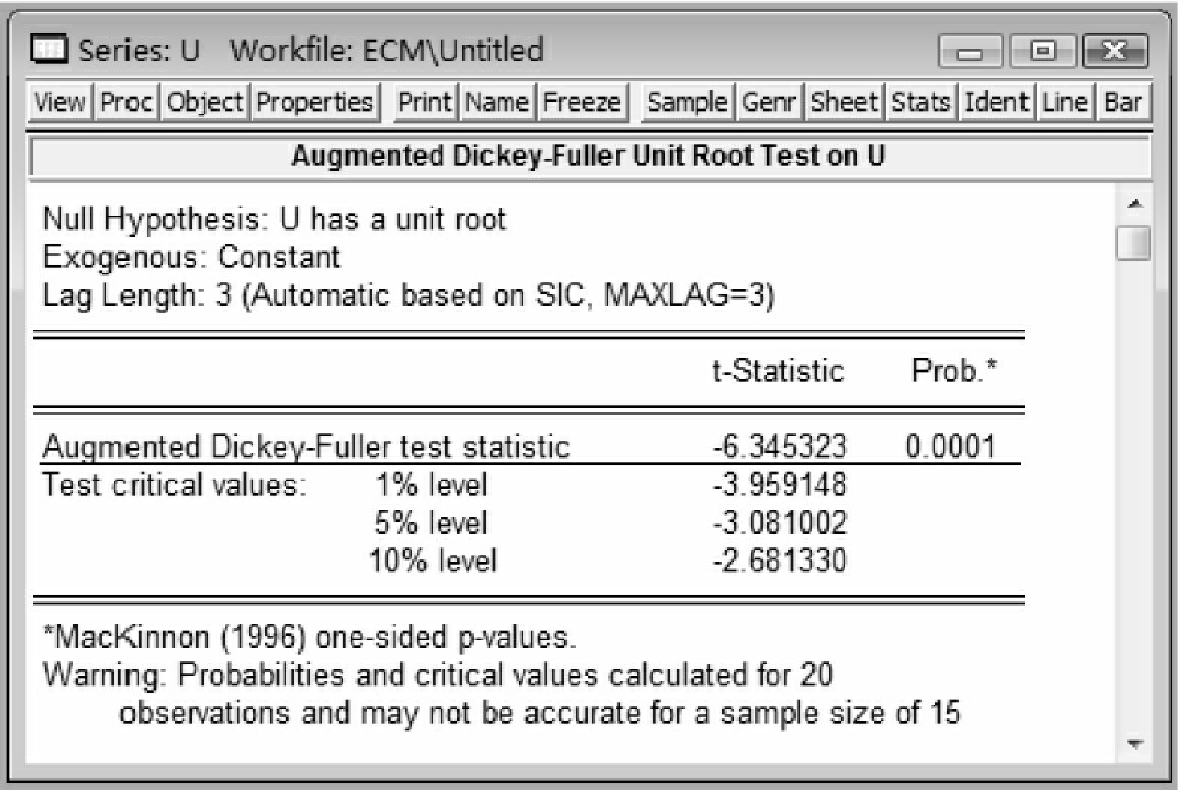
图10-16
⑥协整检验之后,在命令窗口中输入“genr dlnc=d(lnc)”,得到时间序列{ln ct}的一阶差分序列{d ln ct}。同理,得到序列{ln gt}的一阶差分序列{dln gt}。
⑦以稳定的时间序列{ut}作为误差修正项,建立如下模型:
d ln ct=β1·d ln gt+β2d ln gt-1+λut
点击Quick,选择Equation Estimation,在弹出的对话框中输入如下指令:
“dlnc dlng dlng(-1)u(-1)”
其中,dlng(-1)为时间序列{d ln gt}的一期滞后项;u(-1)为时间序列{ut}的一期滞后项,也为模型中的误差修正项,即前一期的非均衡状态对这一期的影响。然后,点击确定得出了模型估计表格,分别如图10-17和图10-18所示。
![]()
到此为止,我们已经完成根据EG两步法进行的误差修正模型的估计。由上述估计式知道,lnCONSP关于lnGDP的短期弹性为1.250。
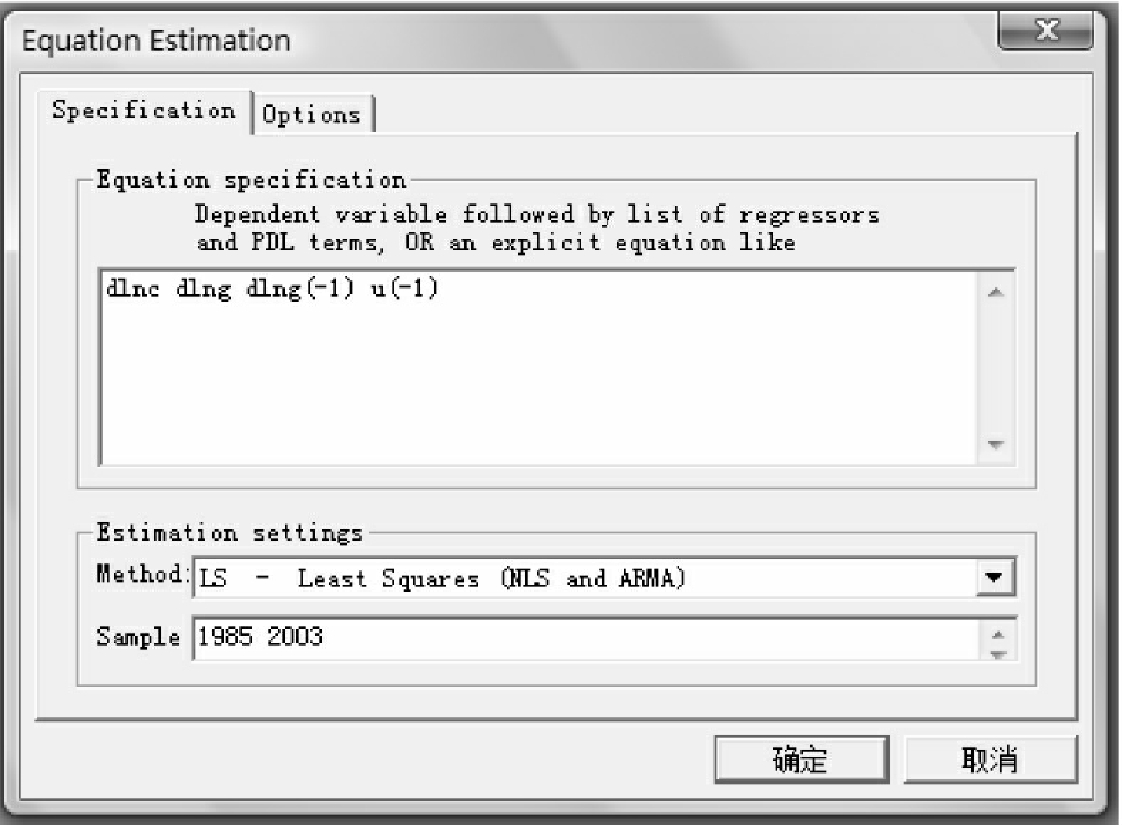
图10-17
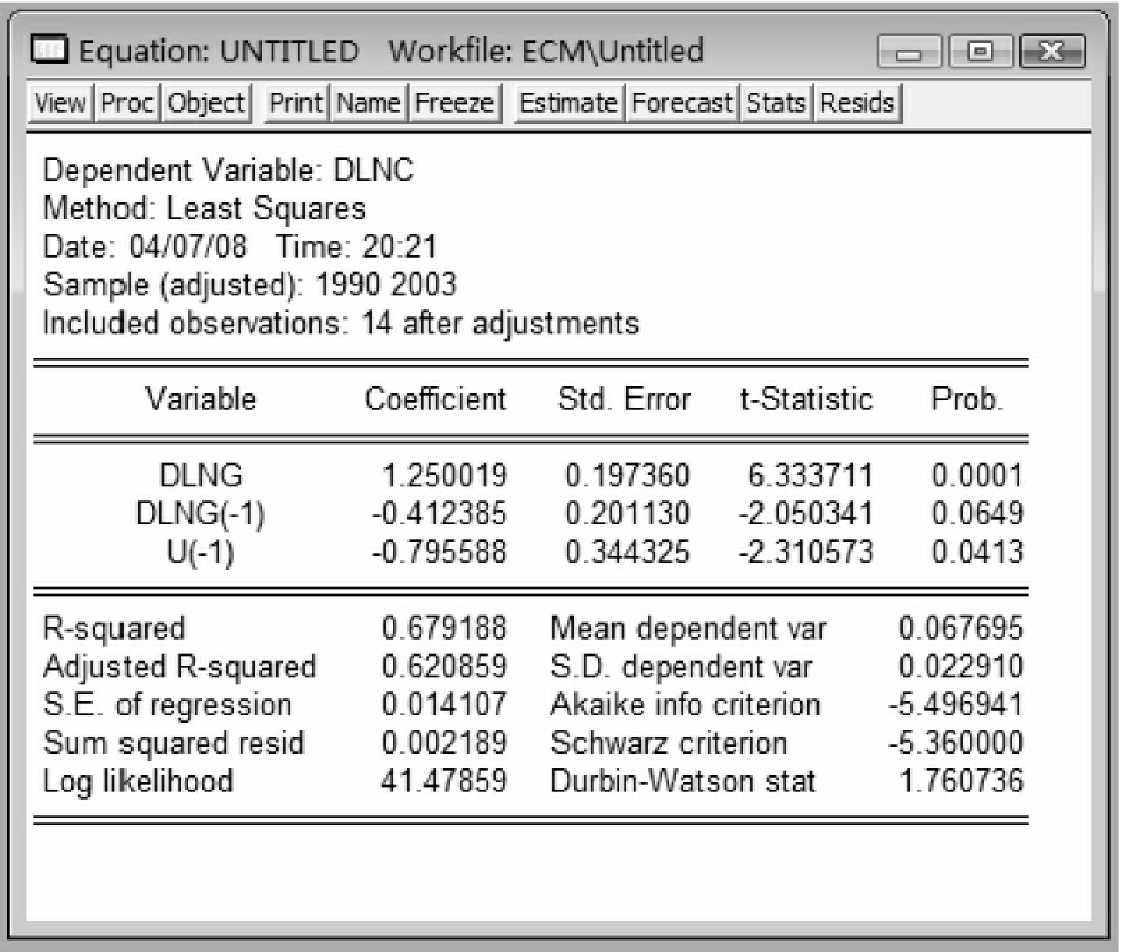
图10-18
⑧打开误差修正项的括号,用直接估计法来直接估计ECM模型,估计式为:
d ln ct=β1·d ln gt+β2·d ln gt-1+λ·ln ct-1+α·ln gt-1同样,如图10-19所示,在EViews操作系统的方程估计对话框中输入如下指令:“dlnc dlng dlng(-1)lnc(-1)lng(-1)”,其中含有(-1)的均为序列滞后一期的值。
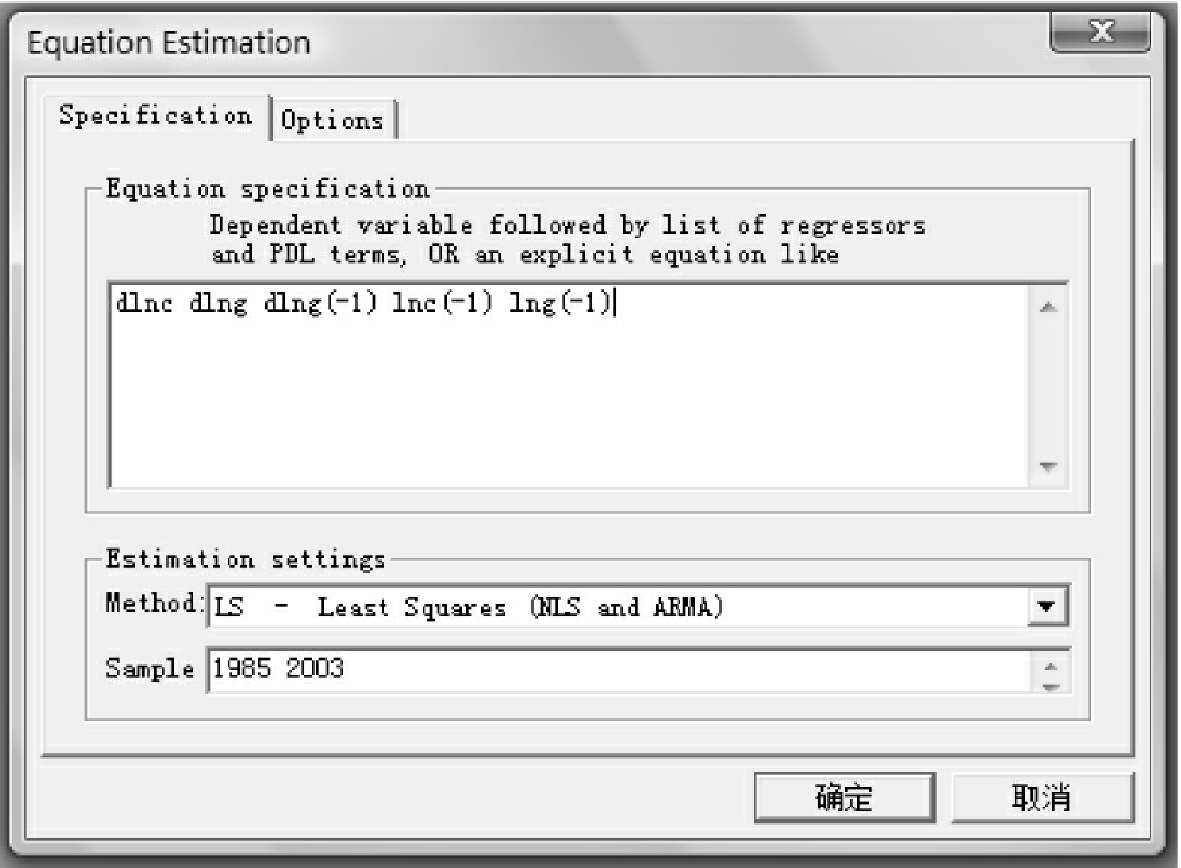
图10-19
⑨直接估计法的结果如图10-20所示。
因此,估计的模型为:
d ln ct=1.441d ln gt
(7.95)
-0.627d ln gt-1(-3.40)-0.262ln ct-1
(-3.72)+0.237ln gt-1
(3.73)
其中,R2=0.854。
将上式写成误差修正模型的形式为:
d ln ct=1.441d ln gt-0.627d ln gt-1-0.262(ln ct-1-0.905ln gt-1)
从以上可以很容易地看出来,lnCONSP关于lnGDP的短期弹性为1.423,ln-CONSP关于lnGDP的长期弹性为0.905。比较EG两步法和直接估计法,两种方法得出的结果非常接近。
有兴趣的读者还可以运用本章第二节的协整模型和本节的ECM模型对2004年中国居民人均消费分别进行预测,并对预测误差进行一个比较。
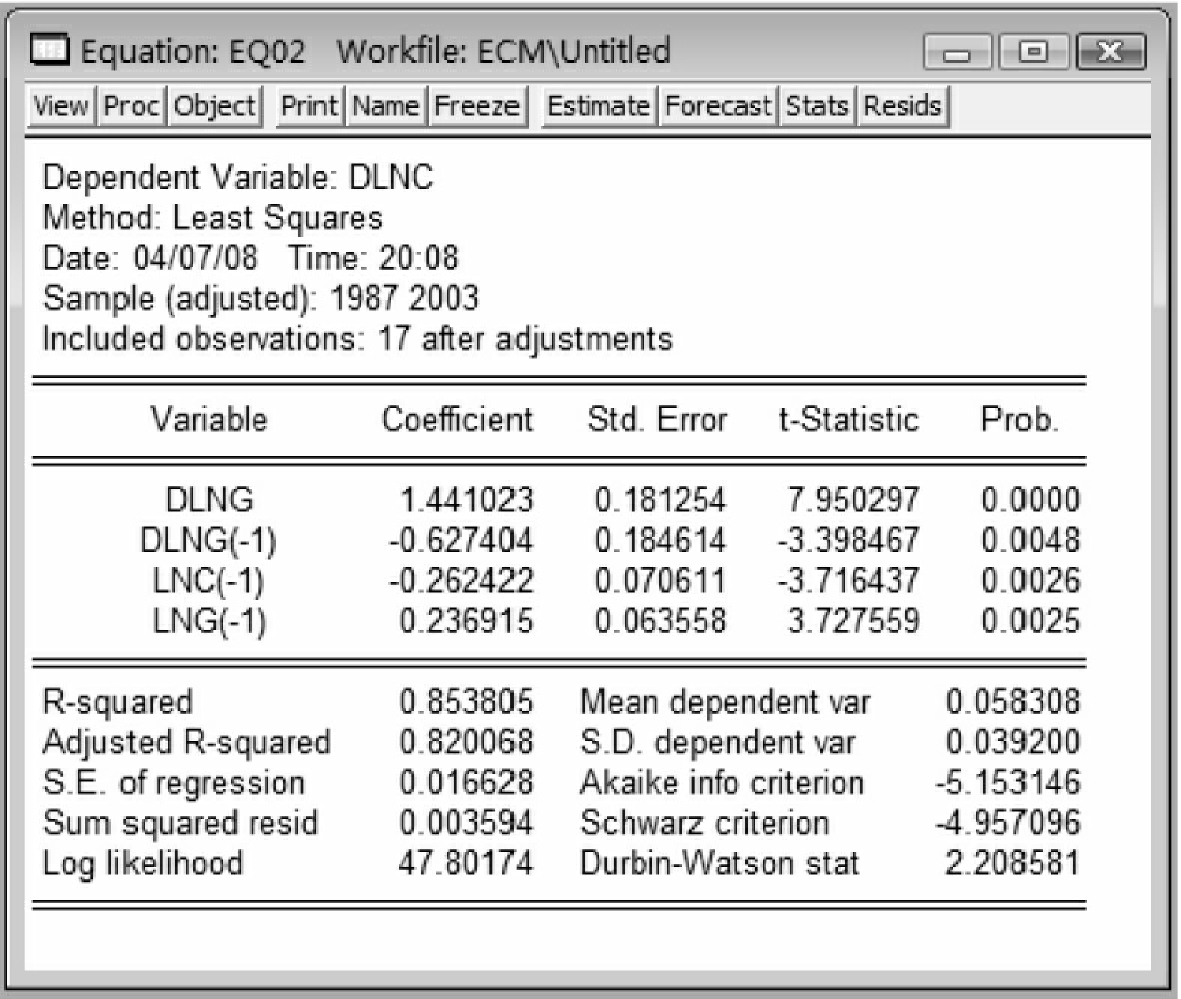
图10-20
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
















