政府部门和私人部门的协商机制

2.2.3　合作形成的催化剂：政府部门和私人部门的协商机制

在群体的形成过程中，达成合作各方共同认可的有约束力的协议，对实现群体各成员之间的有效合作十分重要。而有约束力的协议达成是通过合作成员之间的有效协商来实现的。BT投资建设合同的达成是合作双方不断协商谈判的结果。协商机制在BT模式成功合作中起到关键作用，因此在下一节单独探讨。

1.协商的含义

Muthoo（1999）认为协商是这样一种状况：两个博弈者有共同目标要合作，但利益有冲突的情况下怎样合作^[111]。他进一步指出协商就是怎样达成一个协议的过程，这个过程是一个典型的花费时间和博弈者讨价还价的过程。

一般来说，协商过程实际上是一个谈判过程，是一个利益冲突不断解决，尽可能达成满意协议的过程。通过有效协商，合作各方可以建立一个利益和风险的平衡机制。

2.特许权项目谈判成功的影响因素

国外学者对BOT项目谈判成功的因素进行了探讨。Li Bing等（2005）采用问卷调查方法确认了影响BOT项目谈判的成功因素，认为影响BOT项目谈判成功的关键因素（CSFs）有18个，最重要的前三个因素是：好的私人财团、恰当的风险分配及可利用的金融市场^[112]。Tiong（1996）通过调查，识别出影响BOT项目竞标谈判的六个关键成功因素：企业家和领导，正确的项目说明，私人财团的实力，技术方案的先进性，融资方式，担保的差异性。而且，有吸引力的融资方案在最后的谈判阶段起到非常重要的作用^[113]。通过调查，Tiong和Alum（1997）采用13个融资和合同标准作为谈判的指标，按照他们的研究，认为政府和发起人最看重的前三个因素：项目价格水平、价格未来上涨的趋势及银行和发起人的融资承诺。此外，在最后的谈判阶段，政府和发起人最关心的是项目价格水平^[114]。Ngee L.等（1997）将特许期及价格作为项目回报的解释变量，利用多元回归模型提出了自调整合同谈判机制^[115]。在他们的研究中，自调整合同谈判模型使用35个样本（价格变化幅度每次2％，特许期从10年到14年），先后使用线性回归和非线性回归模型，得出非线性回归模型对变量的解释水平更高（R²=99％），但未考虑项目风险。Shen L.Y.等（2002）回顾了影响谈判的变量，利用期望项目现金流给出了一个定量分析模型^[116]。Fen-May Liou和Chih-Pin Huang（2008）将风险分担加入了BOT项目的谈判模型，并利用蒙特卡罗模拟了项目所有者NPV的概率分布情况，考虑融资高风险和低风险两种情况下，合同谈判模型的变化，并利用台湾ETC项目进行了验证^[117]。研究结果显示：给定NPV情况下，项目发起人高风险时更喜欢长的特许期。

可见，有实力的私人财团、合理的融资方案、合理价格和恰当的风险合配是特许权项目成功合作的关键。

3.协商对策理论（Bargaining-Game Theory）的基本原理

许多学者对协商对策理论作出了贡献，Nash（1950），Raiffa（1953），Harsanyi（1956），Rubinstein（1982），Kreps（1991），Aumann和Brandenburger（1995）和Muthoo（1999）等人对协商对策理论做了深入研究，他们通过博弈分析模型检验协商过程。我们这里主要讨论Rubinstein的模型。

Rubinstein协商博弈分析模型基于下列假设^[118]。

（1）理性行为。两个博弈者，比如政府和私人投资者，按照理性行为行动，也就是说，每个博弈者在博弈过程中获得尽可能多的利益。沿用了Nash给出典型协商博弈：参加者知道每一个策略；每一个策略下支付都可获得；每个参加者都是理性的，最大化自己的利益。

（2）信息共享。参与者分享所有共同的信息。

（3）讨价还价的报酬。协商的报酬可以体现为谈判获得利润、质量、效用的提高。

（4）讨价还价的成本。每一轮谈判中提出反对意见的成本。

（5）时间价值（折现因子）。博弈者都会考虑时间价值，希望尽可能早达成协议。折现因子可以反映出博弈者的隐耐程度（或焦虑程度），隐耐程度越高（或者焦虑程度低），折现因子越大，反之就越小。

Rubinstein用一个假设例子描述了协商过程。假设Smith和Johns共同分一块一单位尺寸的馅饼，协商过程是一个交互式出价方式，也就是，一个参与者Smith首先出价（提出分配方案），另一个参与者Johns可以接受，也可以拒绝，若拒绝，需提出合理的还价方案。给定Smith和Johns的折现因子为δ_s和δ_j，用M和m表示Smith作为出价者可分享的最大和最小利益。

考虑博弈从T期开始，如表2-1所示，Smith获得的最高利益不超过M，因此，Johns将获得1-M的利益。进一步讨论，假设Johns拒绝Smith提出的方案，在T-1期提出还价方案，Smith将接受任何不低于M折现值的出价方案，所以，Johns将提出Smith获得δ_sM，而自己获得1-δ_sM的出价方案。再进一步讨论，在T-2期，Smith知道Johns将拒绝任何低于T-1期获得利益的折现值，因此，Smith提出Johns获得δ_j（1−δ_sM），而自己获得1-δ_j（1−δ_sM）的出价方案。

表2-1　交互式出价的博弈过程

资料来源：Rubinstein A.，Perfect equilibrium in a bargaining model，Econometrics，1982

博弈结束，我们得到Smith分享最大利益的两个表达式，M和1-δ_j（1−δ_sM），因此，得到方程M=1-δ_j（1−δ_sM），解出M=（1−δ_j）/（1−δ_sδ_j）。

另一方面，我们可以重复上述的过程，讨论Smith分享最小利益m时的情况。如果Smith在T期分享利益至少m，Johns在T-1期分享的利益不高于1-δ_sm，那么，Smith在T-2保证自己分享的利益为1-δ_j（1−δ_sm），博弈结束，Smith得到与最大分享利益一致的结果m=（1−δ_j）/（1−δ_sδ_j）。可见均衡的结果是唯一的。

如果Smith先出价，Smith分享的利益均衡值为E（S）=（1−δ_j）/（1−δ_sδ_j），Johns分享的利益均衡结果为E（J）=δ_j（1−δ_s）/（1−δ_sδ_j）

上述的协商博弈模式是一个完全信息下的博弈均衡，尽管实际中信息往往不对称，我们不妨从理想状态出发分析各种经济问题。下面对BT模式合作形成过程的协商机制从政府部门和私人部门信息完全对称状态下进行的。对于信息不对称状态下，合作双方的协商对策模型请参考李会民的博士论文《冲突分析与合作理论研究》^[119]。

4.BT模式合作形成的协商机制分析

BT模式合作形成过程是在BT项目通过招投标（按照我国的招标投标法，政府投资项目应通过招投标确定承包商）确定BT主办人之后进行的，其合作形成的过程就是政府部门与私人部门的协商博弈过程，是冲突不断解决，双方各得其所，各司其职的过程。下面利用Rubinstein协商对策模型对BT合作形成过程分析。

Rubinstein认为在典型的协商博弈过程中，先出价者有一些优势，因此，L.Y.Shen等（2007）将该模型进行了拓展，从博弈双方两个角度分别首轮出价考虑^[120]。我们应用了拓展的模型，假设政府部门BT发起人（政府部门）与BT主办人（私人部门）的合作协商过程分为两种情况：第一种是BT发起人首先提出利益分配方案的协商博弈过程，用来确定BT发起人分享的利益；第二种是BT主办人首先提出利益分配方案的协商博弈过程，用来确定BT主办人分享的利益。

（1）分析过程的假设

①假设BT发起人先提出方案（先出价），BT发起人可分享的最大利益为R_g，最小利益为r_g，BT主办人可分享的最大利益为R_p，最小利益为r_p。

②假设BT主办人先提出方案（先出价），BT发起人可分享的最大利益为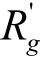，最小利益为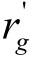，BT主办人可分享的最大利益为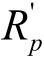，最小利益为。

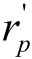③假设BT发起人的讨价还价成本为b_g，BT主办人的讨价还价成本为b_p。

④假设BT发起人和BT主办人的折现因子为δ_g和δ_p。

⑤BT发起人和BT主办人分享的总利益是BT项目建成后所获得的各种效益之和减去BT主办人支付的成本，记为∆R，利用2.3.2节的假设，则，

∆R=R_G1-C_P1-R_P0。

（2）博弈过程分析

①首轮由BT发起人（政府部门）出价

博弈过程如图2-5所示。BT发起人首先出价，要考虑BT主办人可能拒绝并讨价还价的可能性有多大。为减少进一步的讨价还价，节约时间成本，BT发起人对BT主办人的状况进行分析，并提出合理的出价。如果出价对BT主办人没有吸引力，按照理性原则，BT主办人就会拒绝并还价，承担讨价还价成本b_p和时间成本（折现因子δ_p）。因此，可以获得最小利益δ_Pr_P−b_P和最大利益δ_PR_P−b_P。所以，BT发起人第一轮最优出价策略应使BT主办人获得的利益在他的最小利益和最大利益的范围内。这样，BT发起人的最佳出价策略应是获得最小利益为∆R-δ_PR_P−b_P和获得最大利益∆R-δ_Pr_P−b_P。根据前面假设，BT发起人首轮出价中期望的最大利益为R_g，最小利益为r_g，这样得到下面的不等式：

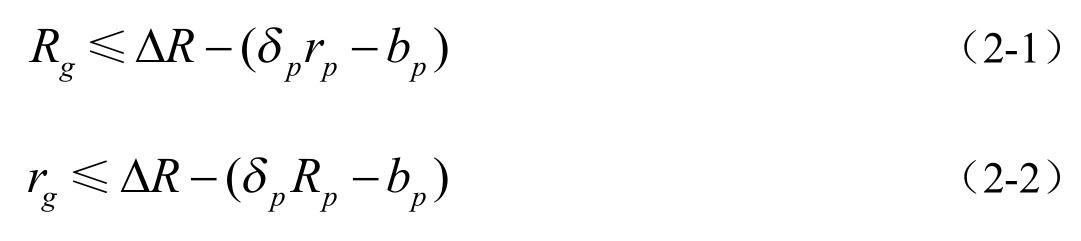
再往下分析，假设BT主办人拒绝BT发起人出价，并进行讨价还价。BT主办人仔细考虑BT发起人的状况后提出合理的还价方案。假设BT发起人拒绝并提出还价方案，则BT发起人承担讨价还价成本为2b_g（包括首轮出价成本）和时间成本（折现因子δ_g）。因此，如果BT发起人再次讨价还价，其获得的最小利益为δ_gr_g−2b_g和最大利益为δ_gR_g−2b_g。考虑到BT发起人可能的还价策略，BT主办人的最佳出价策略是：应使BT发起人获得的利益在他可能还价时获得的最小利益和最大利益的范围之内，即应属于区间[δ_gr_g−2b_g，δ_gR_g−2b_g]。这样，

BT主办人获得最小利益为∆R−（δ_gR_g−2b_g），获得最大利益为∆R−（δ_gr_g−2b_g）。根据前面假设，BT主办人期望的最大利益为R_p，最小利益为r_p，这样得到下面的不等式：

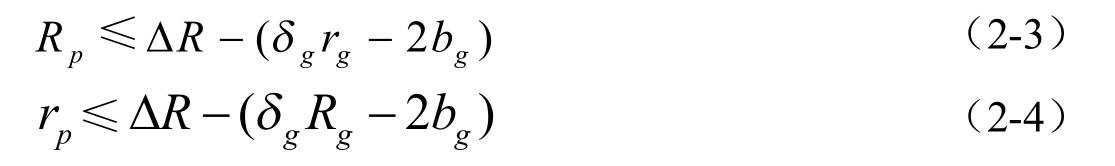
将（2-4）式带入（2-1）式，（2-3）式带入（2-2）式，得到如下的两个不等式：

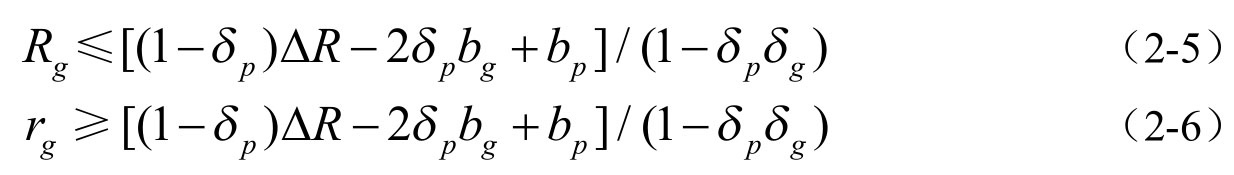
这样，对（2-5）式和（2-6）式分析，BT发起人协商博弈中获得的利益为：

由此确定了BT发起人通过协商博弈获得的利益。

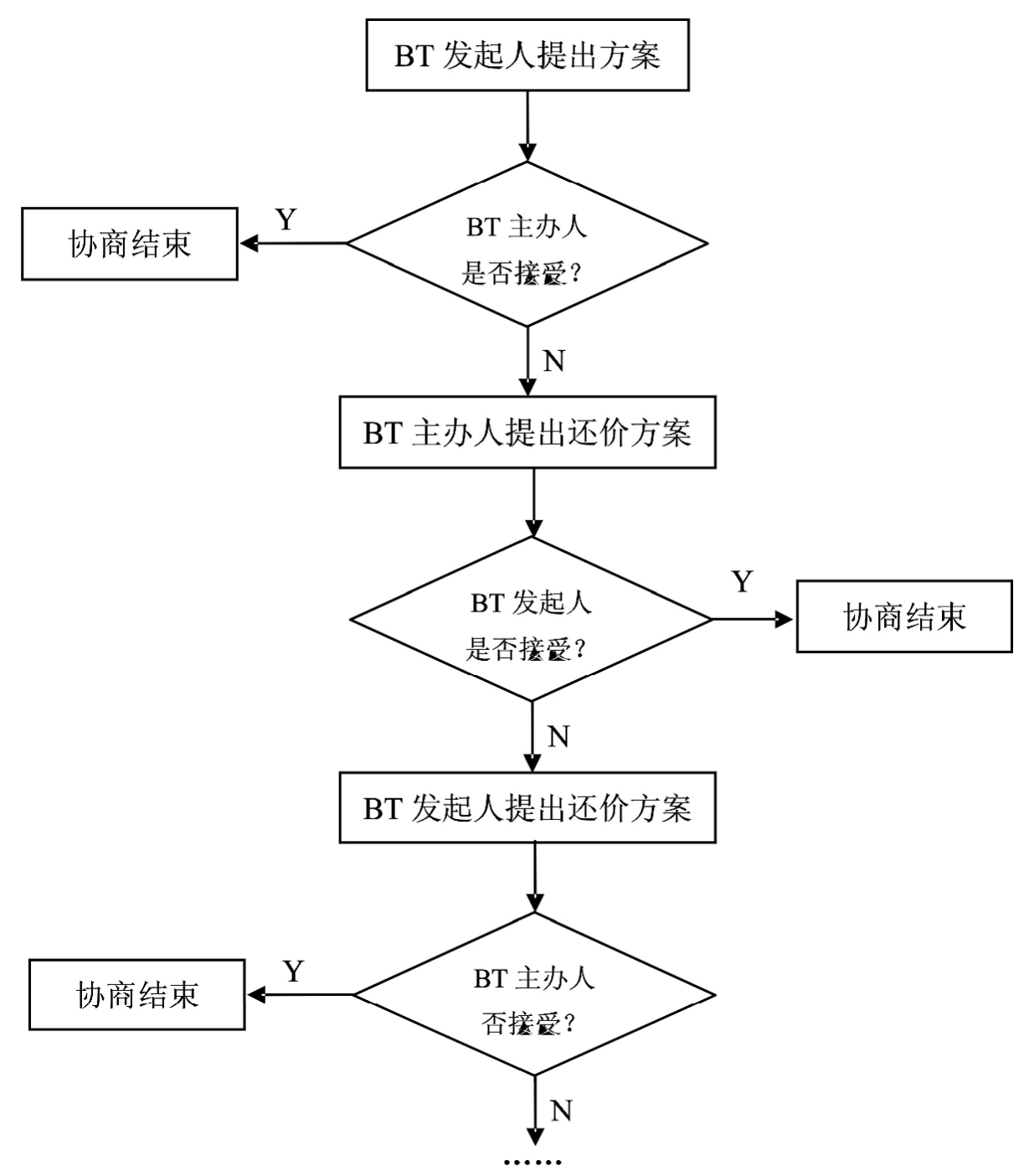
图2-5　BT发起人先出价的协商博弈过程

资料来源：自行绘制

②首轮由BT主办人（私人部门）出价

博弈过程如图2-6所示。BT主办人首先出价，要考虑BT发起人可能拒绝并讨价还价的可能性有多大。为减少进一步的讨价还价，BT主办人对发起人的状况进行分析，并提出合理的出价。如果出价对BT发起人没有吸引力，按照理性原则，BT发起人就会拒绝并还价，承担讨价还价成本b_g和时间成本（折现因子δ_g）。因此，可以获得最小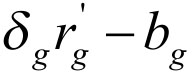利益和最大利益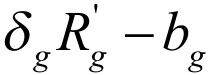。所以，BT主办人第一轮最优出价策略应使BT发起人获得的利益在他的最小利益和最大利益的范围内。这样，BT发起人的最佳出价策略应是获得最小利益为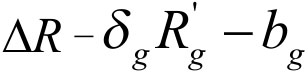和获得最大利益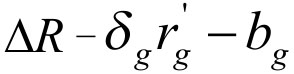。根据前面假设，BT主办人首轮出价中期望的最大利益为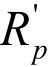，最小利益为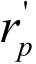，这样得到下面的不等式：

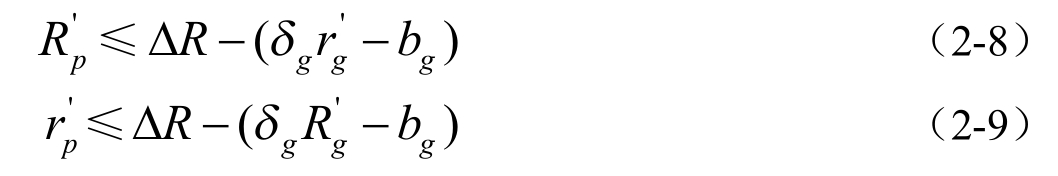
再进一步分析，假设BT发起人拒绝BT主办人出价，并进行讨价还价。BT发起人仔细考虑BT主办人的状况后提出合理的还价方案。假设BT主办人拒绝并提出还价方案，则BT主办人承担讨价还价成本为2b_p（包括首轮出价成本）和时间成本（折现因子δ_p）。因此，如果BT主办人再次讨价还价，其获得的最小利益为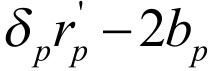和最大利益为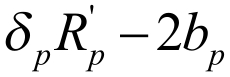。考虑到BT主办人可能的还价策略，BT发起人的最佳出价策略是：应使BT主办人获得的利益在他可能还价时获得的最小利益和最大利益的范围之内，即应属于区间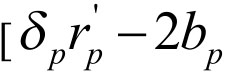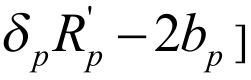，。这样，BT发起人获得最小利益为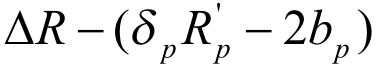，获得最大利益为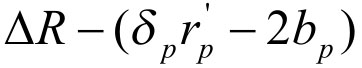。根据前面假设，BT发起人期望的最大利益为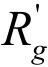，最小利益为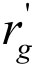，这样得到下面的不等式：

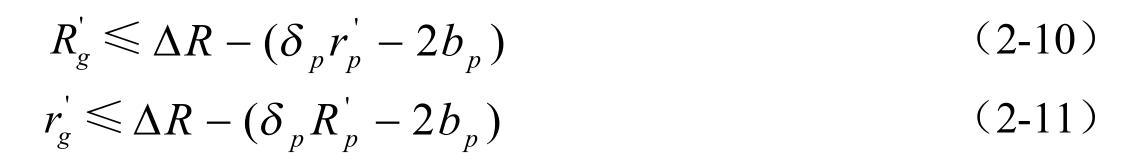
将（2-11）式带入（2-8）式，（2-10）式带入（2-9）式，得到两个不等式：

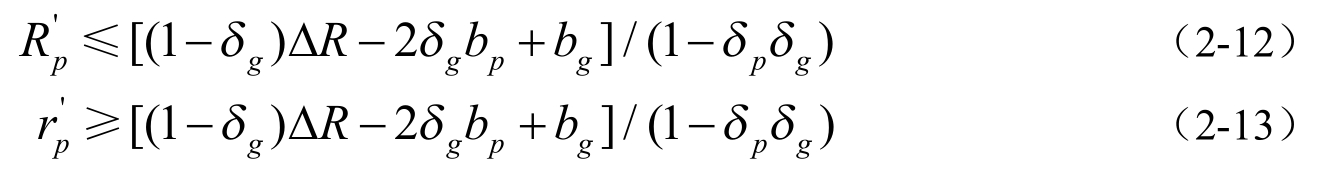
这样，对（1）式和（13）式分析，BT主办人协商博弈中获得的利益为：

由此确定了BT主办人通过协商博弈获得的利益。

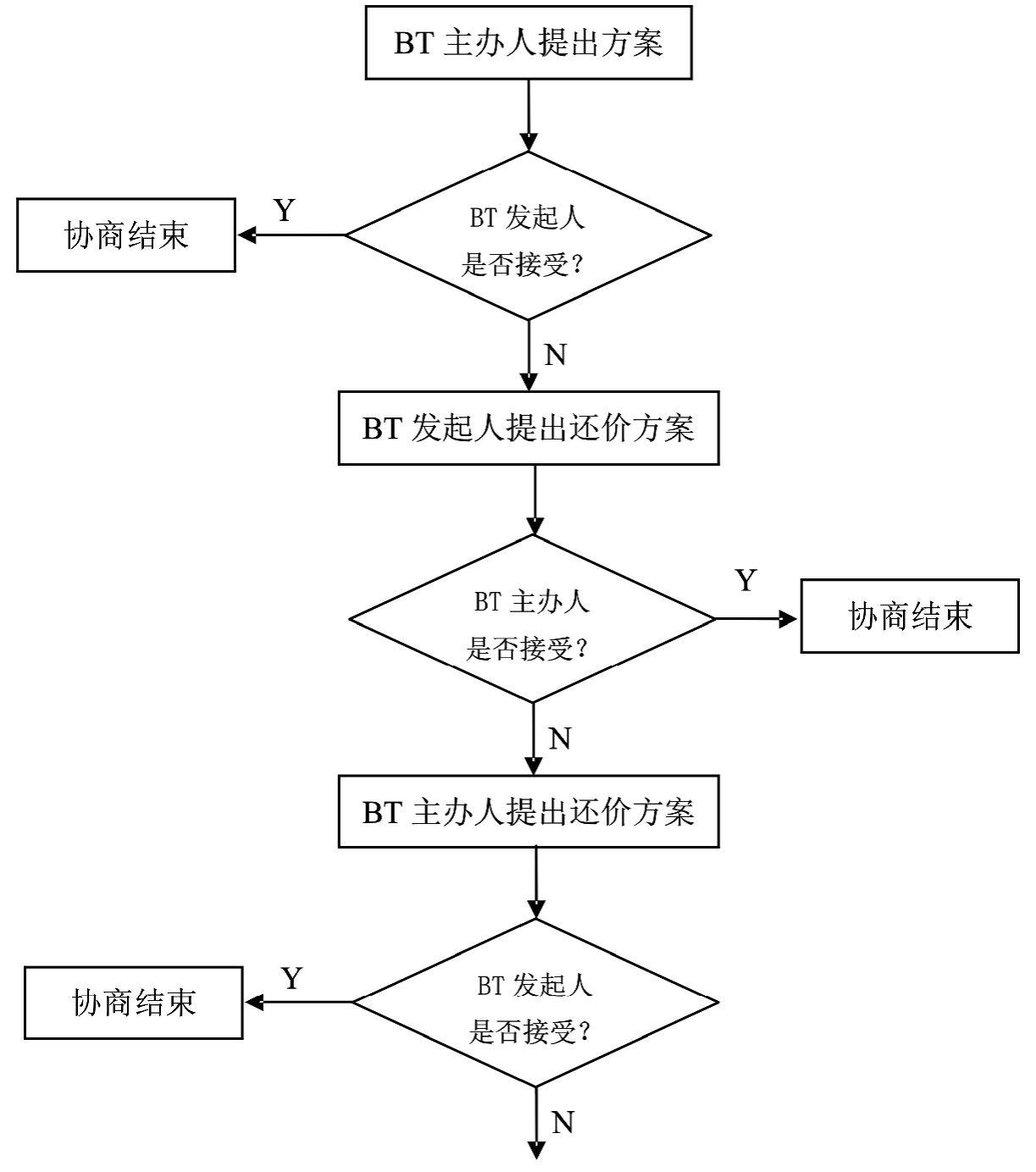
图2-6　博弈过程图示

资料来源：自行绘制

BT模式不但在合同签订之前需要和合同当事人进行谈判，在合同实施过程中，涉及一些变化的事项同样需要进行谈判。前面所述模型可以应用在事前的合同签订过程中，也可用于事后的合同实施过程中。

（3）应用分析

假设某市快速干道采用BT模式建设，招标后BT发起人与BT主办人进行协商谈判。由于该项目不收费，未来没有现金流入，直接的财务效益没有。但该项目对本市发展和改善交通状态非常重要，具有重大国民经济效益和社会效益。假设将这些社会效益折算成价值表示为1.2亿元，BT主办人的投入成本为0.6亿元，其机会成本为0.09亿元（ROI=15％）。这样可知：∆R=1.2-0.6-0.09=0.51=5100万元。

另外，假设δ_g=0.95，δ_p=0.97；b_g=100，b_p=80（单位为万元），之所以假设δ_g≤δ_p，是因为BT项目的发起人更急于找到投资人进行项目建设，隐耐承担低一些；假设b_g≥b_p，是因为政府部门由于官僚成本等原因，其出价成本要高于私人企业。

将上述参数带入公式（2-7）和（2-14），得到下列结果：

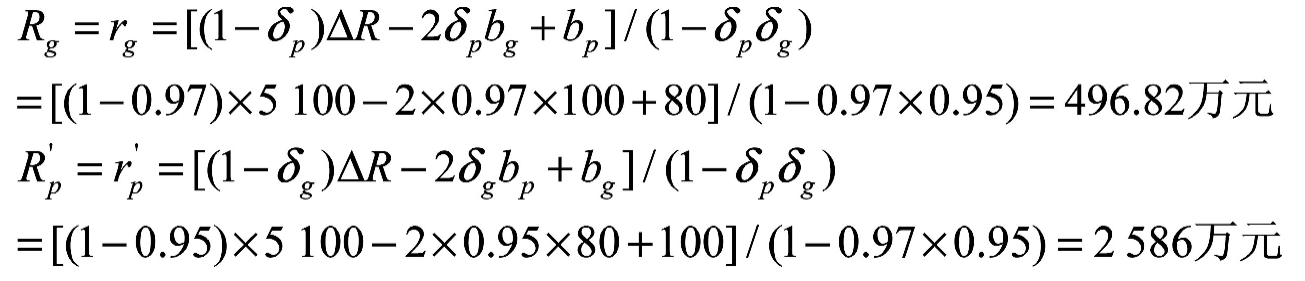
通过BT发起人和主办人的协商博弈，BT发起人分享利益为496.82万元，BT主办人分享利益为2586万元。BT主办人获得的利益高于BT发起人，这与实际情况相符合，因为，BT主办人不投资建设，项目的利益根本不能实现，政府任何利益都不能获得。

上述分析是在完美信息和理性的假设前提下进行的，而实际中信息不对称，个体理性有限，但这不妨碍理性状态下得出结的指导意义，为我们深入研究问题提供一个分析的思路。BT项目通常是没有财务效益的项目，实际中项目实现的价值很难用货币衡量，但私人部门（BT主办人）的投资目标和政府投资控制目标很明确，因此，可以通过二者目标结合，并考虑风险分担的因素，确定BT主办人的投资回报，这部分内容将在后面的章节探讨。