(二)基本理论模型
现在,我们来构造一个网络交易的Akerlof模型或者“柠檬”模型。在模型构建过程中,主要参考了Molho(1997)和Wilson(1979,1980)在分析、扩展Akerlof模型时的部分工具和结论,同时根据前面的讨论,加入买卖双方在网络交易中有关行为特征的进一步规定性。并使用了冯·诺伊曼-摩根斯坦(Von Neumann-Morgenstern)期望效用函数,并考虑在线产品连续质量分布对市场均衡所产生的影响。
我们将网络交易市场分为买方和卖方两部分,并以q∈[q0,q1]表示网络产品的质量,而且它的质量分布函数为f(q)。
分下面几个部分来进行讨论:
1.卖方
对网络销售商(即潜在的卖主)来讲,他的效用函数为:
US=US(c,n│m,q)=c+mqn
这里c为卖主对其他物品的消费;n是离散的二元变量,它表示卖主是否出售产品,n=1表示不出售产品,n=0表示出售产品。m是一种效用指数,反映的是卖主对网络产品的质量的评价(3)。因为影响决策的是绝对价格而不是相对价格,我们可以以p代表产品的价格,把其他商品的价格定义为1。
卖主在收入预算约束下面临的问题是:
maxc,nUS=c+mqn
假定它的预算约束为:
YS=c+pn
这里YS为卖主的收入。当我们把预算约束式代入效用函数后就有:
US=YS+(mq-p)n
如果要使卖主在出售产品(即n=0时)效用最大化,也就是所有者卖掉产品的充要条件是:
![]()
那么,在任何价格下,满足条件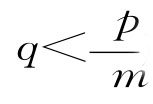 产品所占的比例:
产品所占的比例:
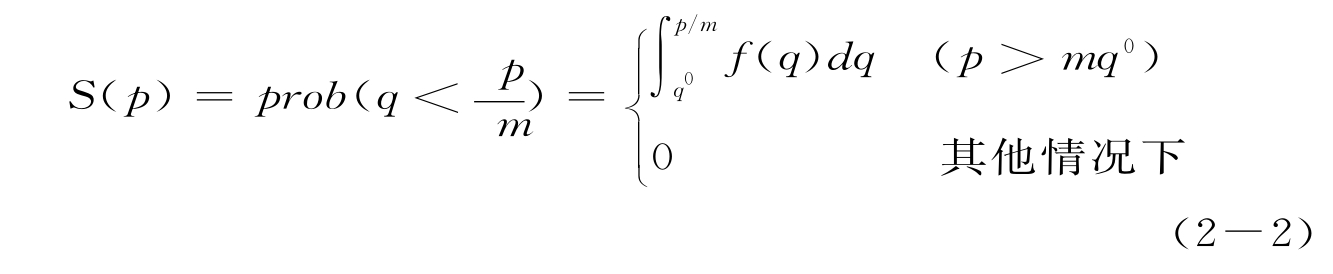
2.买方
对于网络消费者(即潜在的买主)来讲,我们假定他的效用函数为:
UB=UB(c,r│t,q)=c+tqr
这里c为买主对其他物品的消费;r表示卖主是否购买产品的变量,r=1表示购买,r=0表示不购买;t表示网络产品质量与其他物品消费相比的相对评价参数(4),为了保证交易能够顺利进行,应有t≥m。我们同样以p代表产品的价格,而把其他商品的价格定义为1。
买主在收入预算约束下面临的问题是:
maxc,rUB=c+tqr
假定它的预算约束为:
YB=c+pr
这里YB为买主的收入。
与阿克洛夫(1970)模型的基本假定一样,由于消费者并不知道每件产品的实际质量,但可以通过推测和估计等方式来确定产品的平均质量,在网络市场上由于存在着虚拟性则更是如此。因此,我们现在假定在网络市场上产品的平均质量水平为μ。
在存在质量不确定性的前提下,决定他是否购买的决策依据应是期望效用:
E(UB)=c+tE(q)n=c+tμr
这里E(q)所反映的是网络产品的期望质量水平,实际上也就是它的平均质量,即μ=E(q)。
我们把预算约束式代入期望效用函数有:
E(UB)=YB+(tμ-p)r
如果要使买主在购买产品即r=1时效用提高,应有:
![]()
实际上,(2-3)式向我们表明了需求方的决策边界。
3.供需双方可能的均衡结果
和阿克洛夫(1970)模型一样,我们将它的供求函数建立在平均质量与价格的关系之上。按照Wilson(1979,1980)模型,产品价格与平均质量的关系应为:
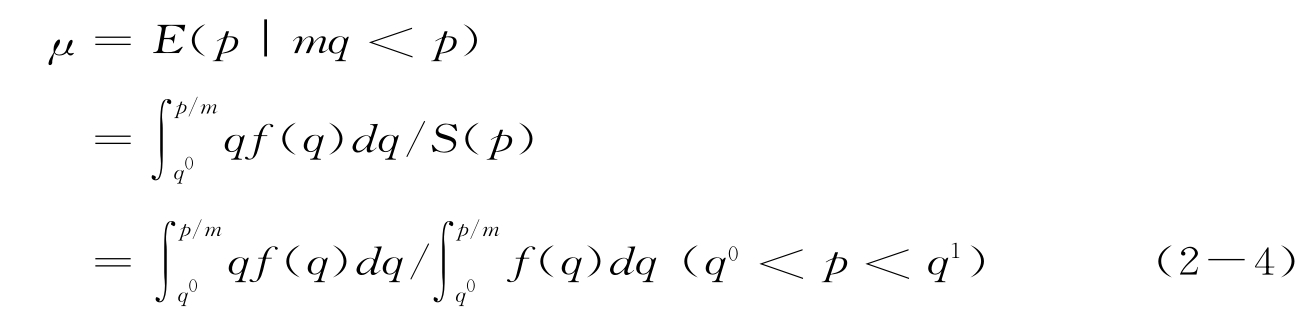
由于它同时满足了(2-1)式的条件,因此,(2-4)式实际上表明了达成交易的产品平均质量水平,更重要的是它表明了供给方的决策边界。将(2-4)与(2-3)式联立,我们就可以分析出供需双方的交易均衡条件,也就是瓦尔拉斯均衡(Walrasian Equilibrium)区域。
为了说明问题,我们赋予产品质量以一定的概率分布,假定q服从均匀分布,则它的密度函数应为:f(q)=1/(q1-q0)。现在,我们根据m的大小分两种情况来讨论市场的均衡和价格的变化:
【情形1】m=1,这样,(2-4)式就变为:
![]()
那么,供需双方可能的均衡结果如图2.1所示。
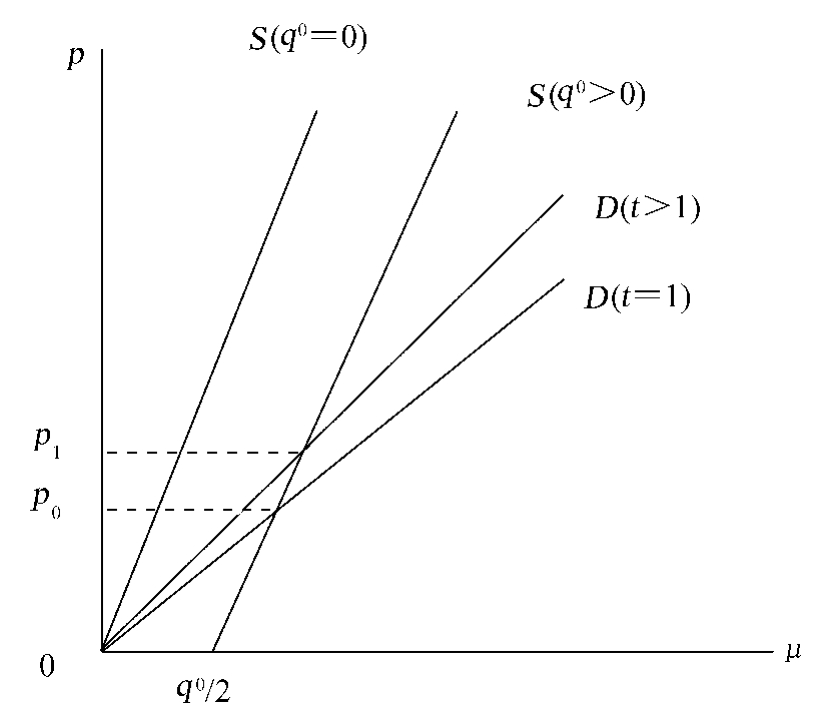
图2.1
在图2.1中,(2-4)式所表达的就是射线S(q0>0)和射线S(q0=0),它是两条质量分布起点不同的供给曲线,反映了供给方的决策意愿和依据。(2-3)式在图2.1中所表达的就是射线D(t≥1)的右下方,它为需求者的决策边界。由前所述,为了保证交易能够顺利进行需要有t≥1,所以,射线D(t=1)为所有表达需求的射线簇D(t≥1)的最低边界。显然,供给区域和需求区域的交集就是瓦尔拉斯均衡区域。这个交集就是曲线D的右下方区域和射线S的交集。
如果网络产品的最低质量为零(即q0=0),相应的S(q0=0)和D(t≥1)的右下方区域的交集也就是惟一可能的均衡为原点(0,0),它实际上已经没有什么实际意义,可以不予考虑。
现在我们来看看最低质量非零的情况(即q0>0)。从图2.1中可以看出,如果消费者由于网络的虚拟性通过降低他对网络产品的质量偏好来弥补他对质量判断不足的话(t值会更加趋近于1),反映在图中就是形成均衡的边界会缩小,所反映的均衡价格会下降(在图中由p1趋于p0)。这就说明,由于网络的虚拟性,网络市场容易形成低价格的均衡。
【情形2】m≠1的情况,则(2-4)式就变为:
![]()
假定卖者对产品质量偏好m≠1,这样将它与(2-3)式联立以后,供需双方可能的均衡范围如图2.2所示。
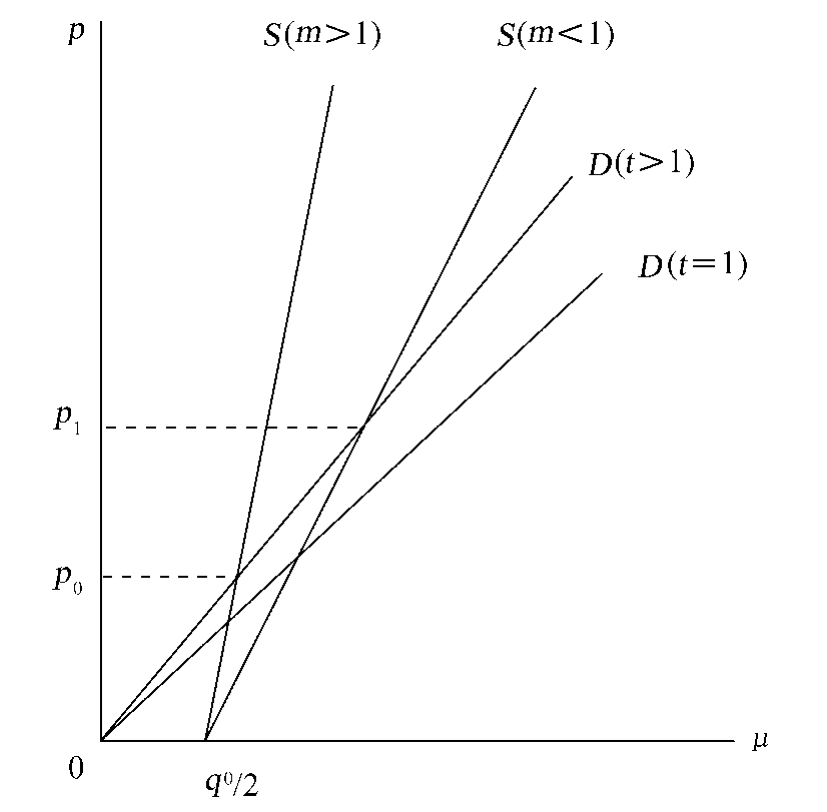
图2.2
从图2.2中我们可以看出,随着m的增加也就是当潜在的网络卖主对产品的质量效用偏好增加时,供给区域也就是射线S和需求区域也就是射线D右下方的交集会缩小,这同样意味着瓦尔拉斯均衡区域在缩小,所反映的均衡价格会下降(在图中由p1趋于p0)。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。













