6.4 房地产收益价格的估算
6.4.1 报酬资本化法的计算公式与收益价格估算
报酬资本化法最一般的计算公式为:
式中 V——房地产在估价时点的收益价格,又称现值;
n——房地产的收益年限或收益期限;
An——相对于估价时点的未来第n期末的房地产净收益;
Yn——相对于估价时点的未来第n期的房地产的报酬率(折现率)。
因为未来各年的净收益及报酬率难以准确预测,在实际估价中难以直接利用,往往只将其作为理论分析工具。该公式中A,Y,n的时间单位是一致的,一般为年。在实际估价中,如果它们之间的时间单位不一致,就要对该公式做相应的调整。另外,如果净收益发生的时间相对于估价时点不是在期末,例如在期中或期初,则应对净收益公式做相应的调整。
实际中,根据报酬资本化法最一般的计算公式,可以推导出以下若干公式:
1)净收益每年不变情况下收益法的公式
净收益每年不变有两种情况:一是收益年限为有限年;二是收益年限为无限年。
(1)收益年限为有限年
收益年限为有限年,其他因素不变的收益法计算公式为:
![]()
式中,V,A,Y,n意义同前。
此公式适用以下条件的估价:房地产的净收益每年不变为A,且收益为有限年期n;报酬率每年不变且大于零,为Y。
【例6.9】 某房地产正常年净收益为50万元,其土地有偿使用年限为60年,已经使用了20年,报酬率为10%。则根据收益法,求该房地产的价格。
(2)收益年限为无限年
收益期限为无限年、其他因素不变的情况下收益法计算公式为:
![]()
此公式适用于以下条件下的估价:房地产的净收益每年不变为A,且收益为无限年期;报酬率每年不变且大于零,为Y。
由于现实条件的限制,收益年限为无限年的公式实际用于评估房地产价格的情况很少,可以说只是一种理想化的情况:第一,我国的土地是国家所有,有使用期限,而且房地产本身也会随着时间的流逝而老化,也有寿命,不能永久地带来收益;第二,报酬率的确定也会随着银行利率和通货膨胀率等各种因素的变化而不断变化,固定不变是不可能的。
【例6.10】 某房地产正常情况下的年净收益为50万元,报酬率为10%,其经济耐用年限为无限年,则按收益法,求该房地产的价格。
【解】 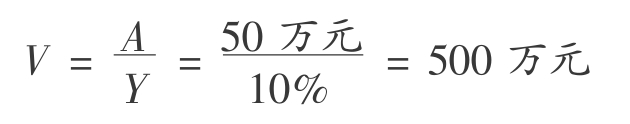
净收益每年不变的计算公式除了直接用于房地产估价外,还有其他用途:
(1)相同房地产不同年限的价格之间的换算
为方便叙述,我们现令:
Kn=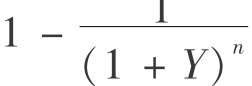 ,表示收益年限为n时的K值;
,表示收益年限为n时的K值;
K∞表示收益年限为无限年时的K值;
Vn表示收益年限为n时的房地产价格;
V∞表示收益年限为无限年时的房地产价格。
我们可以很容易地推导出:
该公式的应用还有一些条件:Vn和VN对应的报酬率相同且不为零;若Vn和VN对应的是不同的房地产,则这两宗房地产除收益年限或土地使用年限不同外,其他各项影响估价的因素都应相同或修正值相同;Vn和VN对应的净收益相同,或可转化为相同,如单位面积的净收益相同。
如果Vn和VN对应的报酬率不相同,但其他因素均符合上述条件时,仍可通过估价公式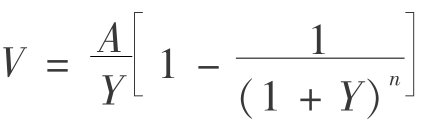 来求得相同房地产不同年限的价格之间的换算。
来求得相同房地产不同年限的价格之间的换算。
【例6.11】 某收益性房地产拥有50年有效收益权,价格为6000元/m2,报酬率为10%,求其30年收益权的价格。
【解】 由公式: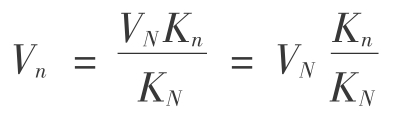
(2)比较不同年限的房地产的价格
如果要比较两宗收益年限或土地使用年限不同的房地产价格,直接比较其价格的高低是不合理的,须将他们转化成相同年限下的价格,这与上述不同期限价格之间的换算方法相同。
【例6.12】 现有甲、乙两宗房地产,甲房地产的单价2000元/m2,收益期限为50年;乙房地产单价1800元/m2,收益年限为30年,若报酬率为10%,试比较这两宗房地产价格的高低。
【解】 为统一比较口径,我们将它们转换为相同期限下的价格。为方便计算,将它们都转换成无限年下的价格:
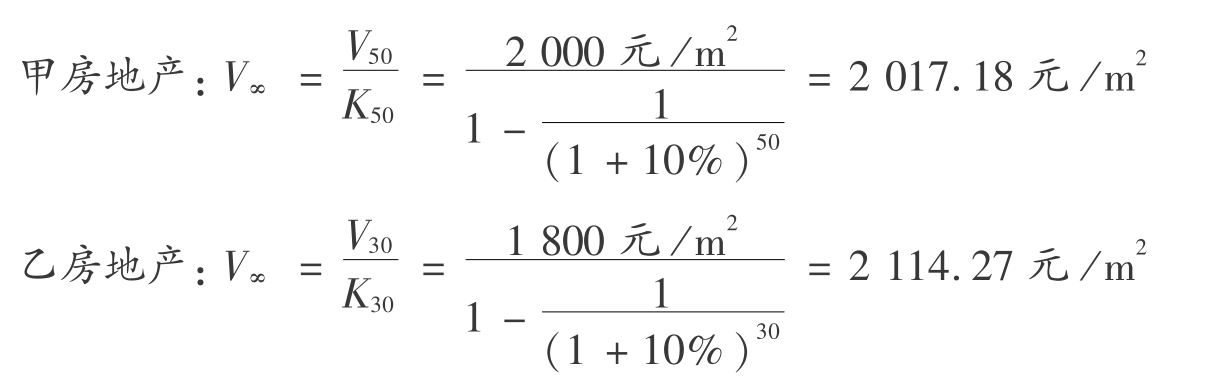
由此可见,虽然名义上乙房地产的价格低于甲房地产的价格,但实际上却高于甲房地产的价格。
(3)其他用途
该公式还能用于市场法中因期限不同进行的价格调整;比较法中土地使用权或收益年期修正;还能用于说明在不同报酬率下土地使用年限长到何时,有限年的土地使用权价格接近无限年的土地使用权价格。通过计算可知,报酬率越高,接近无限年的价格越快。据计算,当报酬率为2%时,要520年才能完全达到无限年期的价格,3%时为350年,4%时为260年,5%时为220年,6%时为180年,7%时为150年,8%时为130年,9%时为120年,14%时为80年,20%时为60年。当报酬率为25%时,只需要50年就相当于无限年时的价格了。
2)净收益在前若干年有变化的情况下收益法计算公式
具体可分为两种情况:一是收益期限为有限年期;二是收益期限为无限年期。
(1)收益期限为有限年期时
![]()
式中,V,A,Y,t,i意义同前。
应用此公式的前提是:净收益年限有限,为n;净收益在未来的前t年(含第t年)有变化,t年以后净收益固定为A;报酬率Y>0且每年不变。
该公式的原型公式为:
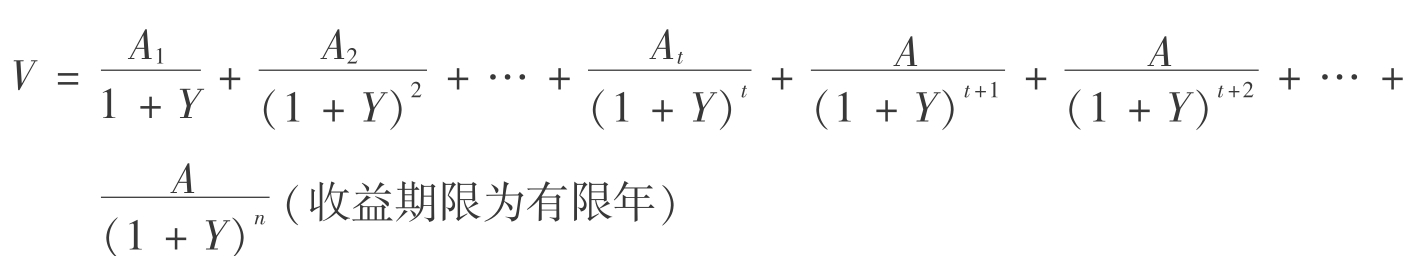
【例6.13】 通过准确预测,某房地产前5年的净收益分别为15,20,23,25,28万元,从第6年到35年每年净收益为30万元,该类房地产的报酬率为10%,求该类房地产的收益价格。
【解】 该房地产的收益价格为:
(2)收益期限为无限年期时
![]()
式中,V,A,Y意义同前;Ai表示第i年的净收益;t表示净收益有变化的年限。
应用此公式的前提是:年期无限;净收益在未来的前t年(含第t年)有变化,t年以后净收益固定为A;报酬率Y>0且每年不变。
该公式的原型公式为:
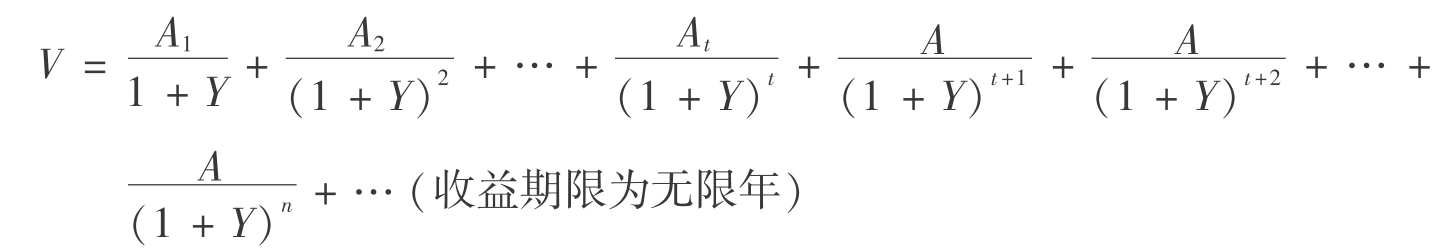
在实际估价工作中,此公式具有重要的实用价值。由于房地产的收益往往每年都是变化的,当我们根据现实情况对房地产未来若干年的收益做出预测时,就可以假设若干年到(如3~5年或更长时间)无限年的净收益保持在一个固定水平,然后对他们分别加以计算,最后加总,求出房地产的总收益价格。
【例6.14】 通过准确预测,某房地产前5年的净收益分别为15,20,23,25,28万元,从第6年到以后无限年每年净收益为30万元,该类房地产的报酬率为10%,求该类房地产的收益价格。
【解】 该房地产的收益价格为:
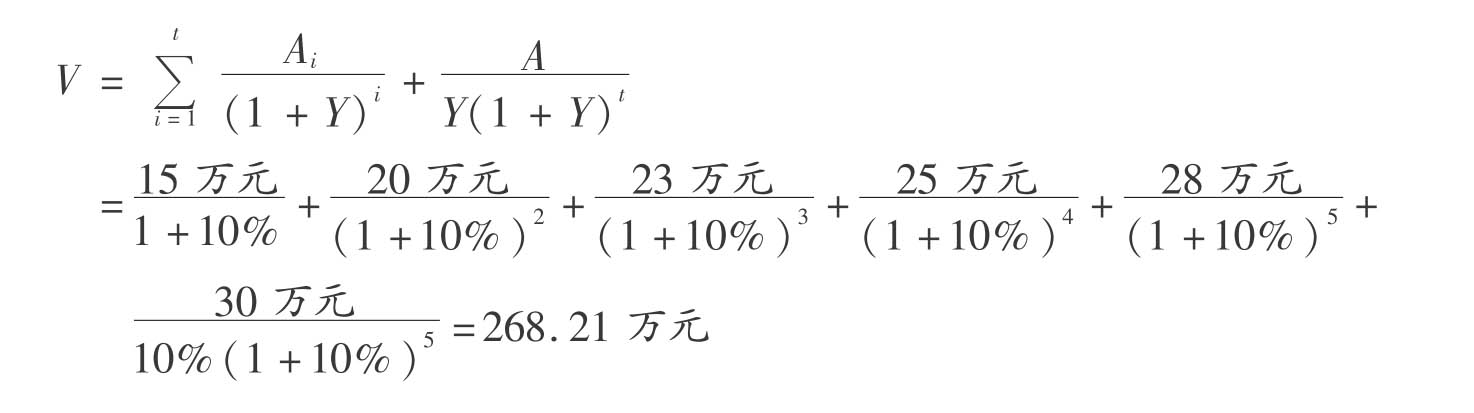
3)净收益前若干年和后若干年都不变,但前、后若干年不同的计算公式
净收益前若干年和后若干年都不变,但前、后若干年不同情况下,房地产价格或价值的计算公式是上述两种情况的混合,具体也可以分为收益有限年和收益无限年两种情况。
(1)收益有限年时
![]()
公式中V,Y,t,i意义同前;A1,A2分别表示前若干年和后若干年的净收益。
应用此公式的前提是:净收益年限有限,为n;净收益在未来的前t年(含第t年)为A1,在未来的t年以后净收益固定为A2;报酬率Y>0且每年不变。
【例6.15】 某商店的土地使用年限为40年,从2006年10月1日起计。该商店共有2层,每层有出租面积为200m2。1层于2007年10月1日租出,租期为5年,可出租面积的租金为180元/(m2·月),且每年不变;2层现暂空置。附近类似商场1,2层可出租面积的正常租金分别为200元/(m2·月)和120元/(m2·月),运营费用率为25%。该类房地产的资本化率为9%。试估算该商场2008年10月1日带租约出售时的正常价格。
【解】 (1)商店1层价格的估算
租约期内年净收益=200m2×180元/(m2·月)×(1-25%)×12月=32.4万元
租约期外年净收益=200m2×200元/(m2·月)×(1-25%)×12月=36.00万元
![]()
=375.69万元
(2)商店2层价格的估算
年净收益=200m2×120元/(m2·月)×(1-25%)×12月=21.60万元
![]()
该商店的正常价格=商店1层的价格+商店2层的价格
=375.69万元+229.21万元=604.90万元
(2)收益无限年时
![]()
式中,V,Y,t,i意义同前;A1,A2分别表示前若干年和前若干年之后无限年的净收益。
应用此公式的前提是:年期无限;净收益在未来的前t年(含第t年)为A1,t年以后净收益固定为A2;报酬率Y>0且每年不变。
4)净收益按等差级数递增或递减的情况下收益法计算公式
这也可以分为收益期为有限年和收益期为无限年两种情况。
(1)收益期为有限年期时
![]()
上式中V,A,R意义同前;n为年期;b为逐年递增或递减额;第1年净收益为A;第2年为(A±b);第3年为(A±2b);第n年为[A±(n-1)b]。
净收益按等差级数递减时只有有限年期一种情况:收益期限为n,且n≤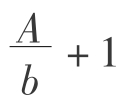 ,因为当
,因为当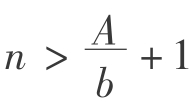 年时,第n年的净收益小于零,显然,任何一个理性的经济人都不会再继续投资。
年时,第n年的净收益小于零,显然,任何一个理性的经济人都不会再继续投资。
应用此公式的前提是:房地产净收益按等差级数b递增或递减(递增时,公式中符号取上面的,递减时取下面的);报酬率大于零且每年固定不变,为Y;收益年期为有限年n。
该公式的原型为:
![]()
【例6.16】 预计某一房地产未来第1年的净收益为33万元,此后每年的净收益会在上一年的基础上减少3万元。该类房地产的报酬率为10%。求该房地产的合理经营期限及该房地产的经营价格。
【解】 该房地产的合理经营期限即每年的净收益都大于零的期限。
令: A-(n-1)b=0
则有:33万元-(n-1)×3万元=0
得: n=12
该房地产的收益价格为:
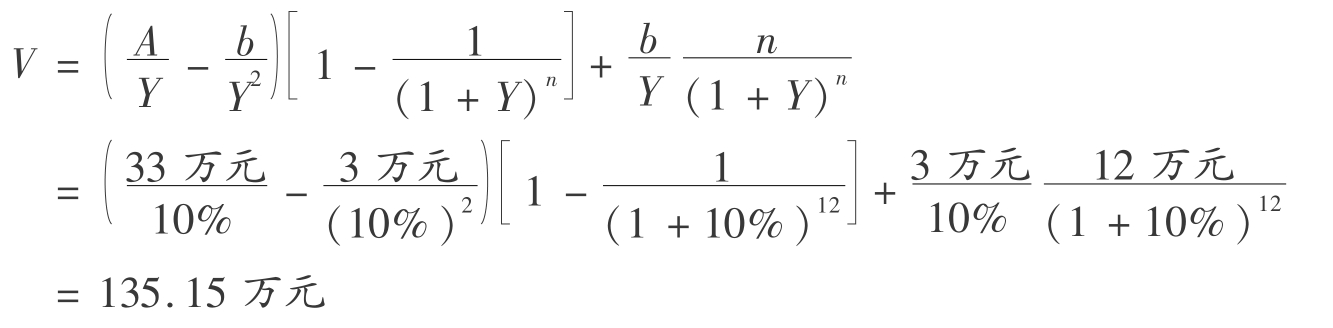
(2)收益期为无限年期时
![]()
式中,V,A,Y,b含义同前。
应用此公式的前提是:房地产净收益按等差级数b递增或递减(递增时,公式中符号取上面的,递减时取下面的);报酬率大于零且每年固定不变,为Y;收益年期为无限年;当净收益递减时,n≤A/b。
该公式的原型为:
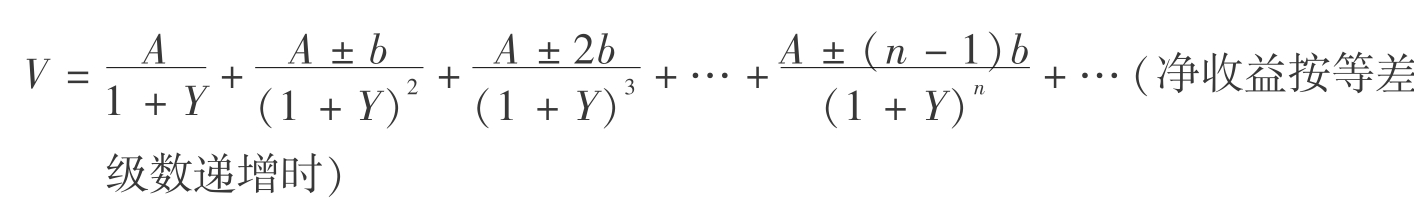
【例6.17】 某一房地产第一年的净收益为25万元,预计以后每年的净收益都在前一年的基础上递增3万元,该类房地产的报酬率为12%,求该房地产的收益价格。
【解】 该房地产的收益价格为:
![]()
5)净收益按一定比率递增或递减的情况下收益法计算公式
这种情况还可分为收益期为有限年和收益期为无限年两种情况。
(1)收益期为有限年期时
![]()
上式,V,A,Y意义同前;g表示净收益每年递增或递减的比率。如第1年的净收益为A,第2年的为A(1+g),第3年为A(1+g)2,第n年为A(1+g)n。
应用此公式的前提是:房地产净收益按等比级数g递增或递减(递增时,公式中符号取加号,递减时取减号);报酬率每年固定不变,为Y,净收益递增时(Y+g)>0;收益年期为有限年n;净收益递增时,g≠Y。
该公式的原型为:
![]()
【例6.18】 某一房地产第1年的净收益为20万元,预计此后每年的净收益都比上年的递增7%,该房地产的使用年限还剩下30年,该类房地产的报酬率为12%,求该房地产的收益价格。
【解】 该房地产的收益价格为:
(2)收益期为无限年期时
![]()
上式,V,A,Y,g,n意义同前。
应用此公式的前提是:房地产净收益按等比级数g递增或递减(递增时,公式中的符号取上面的,递减时则取下面的);报酬率Y每年固定不变且不为零,净收益递增时Y>g,递减时(Y+g)>0;收益年期为有限年n。
该公式的原型为:
![]()
【例6.19】 某一房地产第1年的净收益为20万元,预计未来各年的净收益均逐年递增7%,该类房地产的报酬率为12%,求该房地产的收益价格。
【解】 该房地产的收益价格为:
![]()
6)预知未来若干年后的房地产价格的收益法计算公式
公式原型为:
![]()
上式,V,A,Y意义同前;t表示年限;Vt表示未来第t年的房地产价格。
应用此公式的前提是:已知房地产在未来第t年末的价格为Vt;房地产在前t年(含第t年)的净收益有变化且已知;在预知年限范围内具有相同的报酬率Y,且大于零。
若净收益为A,且每年不变,则上述公式可变为:
![]()
一般来说,在实际应用该公式时,有以下两种情况:一是房地产所处区域的发展情况,如城市规划或社会经济地理位置的改变等,房地产所处地区行情将会有较大变化,比较容易预测待估价房地产未来某一时期的价格或者未来价格相对于当前价格的变化率时;二是对一些收益期特别长的房地产,往往先确定其合理的持有期,并预测持有期间的净收益和持有期末的价值,最后折算为现值。
【例6.20】 某一城市相对欠发达区的房地产目前的价格水平约为3000元/m2,年净收益为300元/m2,报酬率为10%。按最新的城市规划,5年后该地区将建成一个重点商业区,届时该地区可达到该市现有著名商业区的水平。在该市现有的著名商业区,同类房地产的价格为5000元/m2,预计该地区按规划建成后房地产价格可达到5000元/m2。求获知将建商业区的消息后该地区房地产的价格。
【解】 获知将建商业区的消息后该地区房地产的价格为:
这一价格比目前的价格水平高1241.84元/m2。
【例6.21】 预计某房地产未来3年的净收益分别为50,60,70万元,且3年后的价格将比现在上涨6%,该类房地产的报酬率为12%。求该房地产现在的价格。
【解】 该房地产现在的价格为:
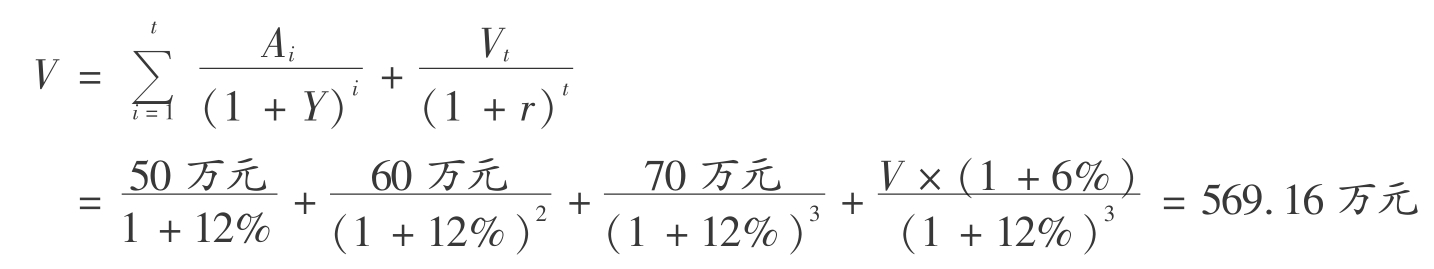
【例6.22】 某房地产目前的年净收益为300万元,且预计4年内仍将维持该水平,4年后将其转卖,售价将达到8000万元,销售税费为售价的5%。若该类房地产的报酬率为12%,求该房地产目前的价格。
【解】 该房地产目前的价格为:
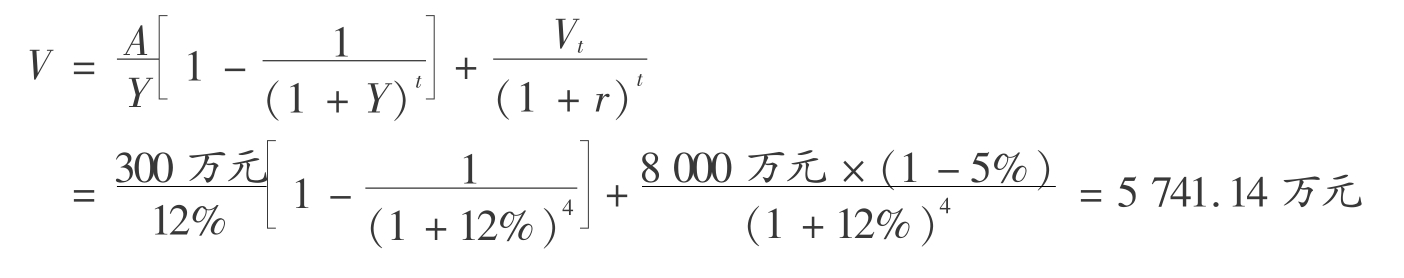
总之,我们在使用报酬资本化法估算房地产价格时,可以根据不同情况选用上述几种公式,这些公式都是从报酬资本化法的最基本公式中推导出来的,所以理论上没有问题,只是在实际应用中,一定要注意各个公式的使用条件,以免出现错误。
6.4.2 直接资本化法的计算公式与收益价格估算
利用资本化率将年收益转换为价值的直接资本化法的常用公式为:
![]()
式中 V——房地产价值;
NOI——房地产未来第1年的净收益;
R——资本化率。
利用收益乘数法将年收益转换为价值的直接资本化法公式为:
房地产价值=年收益×收益乘数
收益乘数具体有以下4种类型:
●毛租金乘数 毛租金乘数(Gross Rent Multiplier,GRM)是市场上的价格除以毛租金(年毛租金或月毛租金)所得的倍数,即通常所称的“租售价比”。
●潜在毛收入乘数 潜在毛收入乘数(Potential Gross Income Multiplier,PGIM)是市场上的价格除以其年潜在毛收入所得的倍数。
●有效毛收入乘数 有效毛收入乘数(Effective Gross Income Multiplier,EGIM)是市场上的价格除以其年有效毛收入所得的倍数。
●净收益乘数 净收益乘数(Net Income Multiplier,NIM)是市场上的价格除以其年净收益所得的倍数。
与收益乘数相对应,收益乘数法有毛租金乘数法、潜在毛收入乘数法、有效毛收入乘数法和净收益乘数法4种类型。
●毛租金乘数法 毛租金乘数法是将估价对象未来某一年或某一月的毛租金乘以相应的毛租金乘数来求取估价对象价值的方法。即:
房地产价值=毛租金(GR)×毛租金乘数(GRM)
●潜在毛收入乘数法 潜在毛收入乘数法是将估价对象某一年的潜在毛收入乘以相应的毛租金乘数来求取估价对象价值的方法。即:
房地产价值=潜在毛收入(PGI)×潜在毛收入乘数(PGIM)
●有效毛收入乘数法 有效毛收入乘数法是将估价对象某一年的有效毛收入乘以相应的有效毛收入乘数来求取估价对象价值的方法。即:
房地产价值=有效毛收入(EGI)×有效毛收入乘数(EGIM)
●净收益乘数法 净收益乘数法是将估价对象某一年的净收益乘以相应的净收益乘数来求取估价对象价值的方法。即:
房地产价值=净收益(NI)×净收益乘数(NIM)
利用资本化率将年收益转换为价值的直接资本化法的常用公式也可以用来求取资本化率R:
![]()
这里的资本化率R实际上是一种综合资本化率(R0)。它还可以表示为:
![]()
推导过程如下:
将本公式等式两边的分子和分母同时除以有效毛收入(EGI),则
![]()
又因为 NOI/EGI=NIR,V/EGI=EGIM
所以 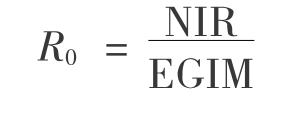
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















