数学曲线拟合法原理与应用

8.4　数学曲线拟合法原理与应用

8.4.1　数学曲线拟合法的原理

为了算出逐期的趋势值，可以考虑对房地产历史价格数据拟合一条数学曲线方程，这就是数学曲线拟合法。在用数学曲线拟合法测定趋势值时首先要解决的问题，是曲线方程的选择。选择曲线方程有两个途径：一是以时间X为横轴，房地产价格Y为纵轴的直角坐标图上做时间序列数值的散点图，根据散点的分布形状来确定拟合的曲线方程；二是对时间序列的数值做一些分析，根据分析的结果来确定应选择的曲线方程。通常采用第一个途径，因为它比较简单、易于理解。选择合适的方程，是估价人员在分析预测时应特别注意的问题。

曲线方程主要有直线方程、指数曲线方程和二次抛物线方程，因此，数学曲线拟合法主要有直线趋势法、指数曲线趋势法和二次抛物线趋势法。其中最简单、最常用的是直线趋势法。这里仅介绍直线趋势法。

当估价对象或类似房地产的历史价格在直角坐标图上的散点图，其图形近似于一条直线时，可用直线趋势法评估房地产的价格。

直线趋势法评估房地产价格的数学方程是：

Y＝a＋bX

式中　Y——表示各时期的房地产价格；

X——表示时期；

a，b——未知的常数。

运用直线趋势法评估房地产价格的关键是确定a，b的值。根据最小二乘法，求得a，b的值分别为：

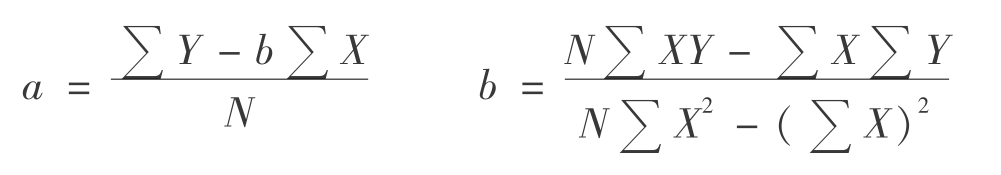
当钞X＝0时，确定a，b值的公式可以简化为：

其中，n为时间序列的项数；钞X，钞X²，钞Y，钞XY的数值可以分别从价格实际值和时间序列值中求得。

实际计算中，为减少计算的工作量，可使钞X＝0。其方法是：当时间序列的项数为奇数时，设中间项的X＝0，中间项之前的项依次设为－1，－2，－3，…，－n，中间项之后的项依次设为1，2，3，…，n；当时间序列的项数为偶数时，以中间两项相对称，前者依次设为－1，－3，－5，…，－n，后者依次设为1，3，5，…，n。

8.4.2　数学曲线拟合法的应用

这里仅以直线趋势法的例子讲一下数学曲线法的应用。

【例8.5】　某经济不发达地区的某房地产2005—2011年的价格见表8.9，试用直线趋势法预测该房地产2012年的价格。（暂不考虑最新政策的影响）

表8.9　某房地产2005—2011年的价格单位：元/m²

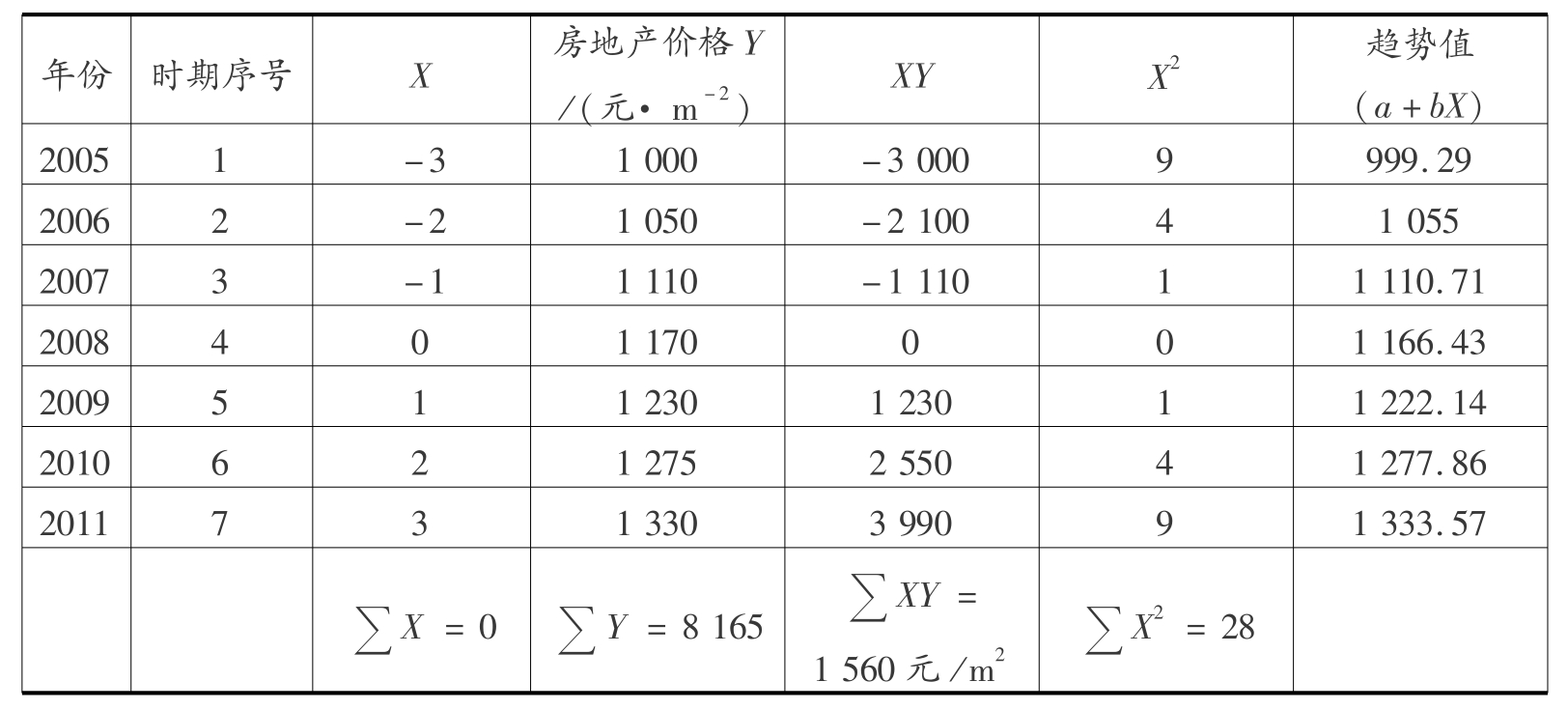
【解】　N＝7，X的取值分别为：－3，－2，－1，0，1，2，3，这样使得钞X＝0。

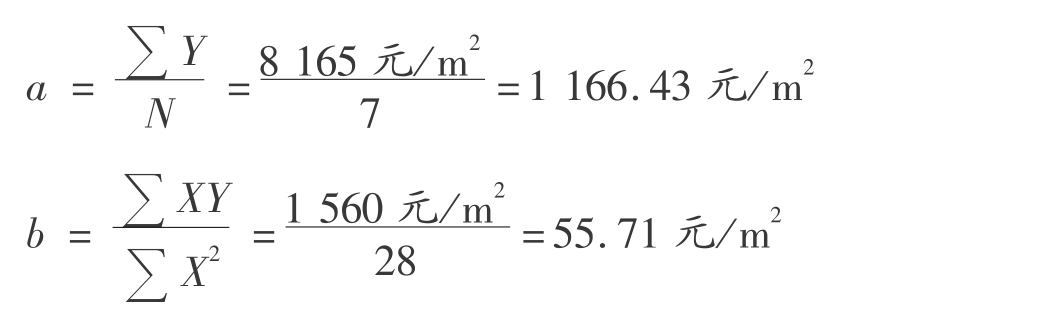
因此，描述该房地产价格变动的长期趋势线的具体方程为：

Y＝a＋bX＝1166.43元/m²＋55.71X

根据这个方程预测该房地产2012年的价格为：

Y＝1166.43元/m²＋55.7元/m²×4＝1389.27元/m²

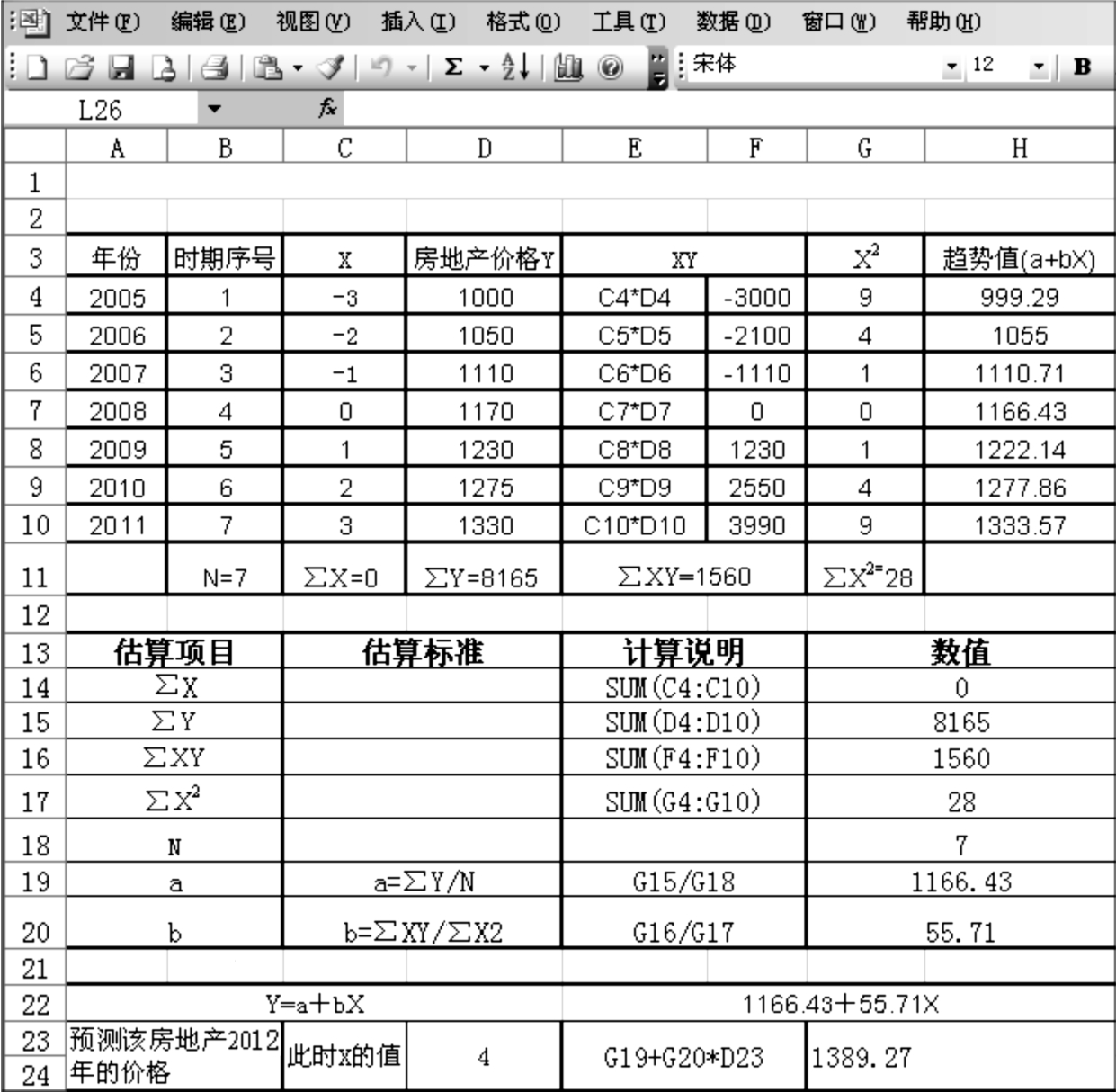
利用Excel表格形式，上述做法简示见表8.10。

表8.10　某房地产2005—2011年的价格单位：元/m²