σ的度量指标及计算

第三节　6σ的度量指标及计算

一、6σ管理中的几个常用指标

1．σ：这是一个希腊字母，用来度量质量特性波动大小统计单位，在统计学中称为标准差。任何一个质量特性X总是有波动的，这种波动是随机的，时隐时现，时大时小，时正时负。但是当大量观察了同一质量特性时，隐藏在随机性后面的统计规律性就会显现出来，这就是X的概率分布。在一个特性的概率分布中，有两个重要的特征量，这便是随机变量的均值与标准差。随机变量的均值（统计中记为E（X））常用希腊字母μ表示，随机变量的取值与均值的差，称为偏差，反映了波动，由于这种偏差也是随机的，为避免正负抵消，用它的平方的均值〔统计中记为Var（X）＝E（X－E（X））²〕来表示其大小，称为方差，记为σ²，方差的算术根便是标准差，记为σ。

2．过程能力PC与过程能力指数C_p。

（1）过程能力是指过程加工质量方面的能力。这种能力表示过程稳定的程度，在过程受控时，特性服从的分布是正态分布。过程的稳定性可以用标准差σ来度量，σ越小，过程越稳定，过程能力越高。由于在受控过程中，特性值有99．73%散布在（μ－3σ，μ＋3σ）内，因此将过程能力定义为：

PC＝6σ

（2）过程能力指数是用来度量一个过程满足顾客要求的程度。顾客的要求可以用规范限来表示。顾客对规范的要求可以是双侧的，即要求在X在（LSL，USL）内。若记规范限的宽度为T＝USL－LSL，规范的中心为M＝（USL＋LSL）／2，当规范中心M与过程中心μ重合时，定义过程能力指数为顾客要求与过程能力之比：

有时顾客的要求是单侧的。如果顾客要求X必须大于LSL时，就定义过程能力指数为：

如果顾客要求X必须小于USL时，就定义上过程能力指数为：

在顾客的要求是双侧规范限时，过程中心μ不一定与规范中心M重合，那么这时实际的过程能力指数用C_pk表示：

C_pk＝min｛C_pU，C_pL｝

C_pk的其他计算公式有：

C_pk＝（1－K）C_p＝（T－2ε）／6σ

式中：ε＝｜M－μ｜是中心的偏移；K＝2ε／T是偏离度。由于C_pk≤C_p，因此C_p又称为潜在的过程能力指数。

（3）长期的过程能力指数与短期的过程能力指数。在实际中上述涉及的参数μ与σ常常是未知的，需要从过程中抽取数据获得它们的估计。

在短期的过程能力指数中，可以从短期获得的数据来估计。譬如在一个稳定的过程中每隔一定时间从生产线上连续抽取一个n产品测定其特性值，从中可以计算它的平均值μ，极差R（或标准差s），如果抽取了k组，那么可以得到μ和σ的估计如下：

上面的d₂与c₄是一个修偏系数，他们与n有关，可以查表得到。

长期过程能力指数也称为过程性能指数，记为P_p相应的有P_pk，P_pU，P_pL，只是其中的μ和σ的估计改变了。将长期收集的所有数据看成为一个样本。它的样本很大，常有几百、几千个。若记总的数据个数为N，那么记其平均值为μ，样本标准差为s，可以直接用它们来估计μ和σ：

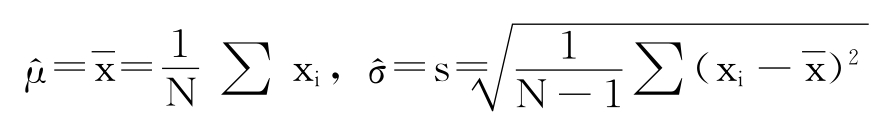
其中s无需修正，因为样本量很大，要注意σ的估计在长期数据场合已不能用平均极差或平均标准差估计了。

规范限内所包含的σ个数与不合格品率的关系：

在过程稳定时，若给出了规范限，过程的平均与标准差后，我们可以通过查正态分布表，获得不合格品率。这里给出一张在不同的δσ质量水平下对照表——每100万个产品中的不合格品数。

设规范限为（LSL，USL），规范限的宽度为T，规范的中心为M，过程的均值为μ，标准差为σ。见表14－1。

表14－1　σ个数与不合格品率的关系

3．单位产品的平均缺陷数DPU。设X表示单位产品上的缺陷数，那么它服从泊松分布，其平均值常用μ表示，而在一些文献上称它为DPU，表示的是单位产品上的平均缺陷数。此时合格率为：

P（X＝0）＝e^－DPU

因此要提高合格率就要降低DPU。

4．每个机会的缺陷数DPO与百万个机会的缺陷数DPMO。一件产品上有10个位置可能产生缺陷，并且每个位置上最多出现一个缺陷。此种位置称为一个机会（oppor－tunity）。如一块印刷电路板上有50个焊点，那么虚焊、漏焊、焊锡过多等缺陷只能出现在这50个位置上，这50个位置就是50个机会。又如护士在病房里护理病人，早、中、晚三次送药片，输药水、记录体温等方面可能发生差错。这些方面就是缺陷可能出现的机会。假如一个产品（或一项服务）有10个机会，可用10个长方格表示机会，缺陷可用“●”表示。

若抽取60个这样的产品共发现18个缺陷，每个机会的（平均）缺陷数定义为：

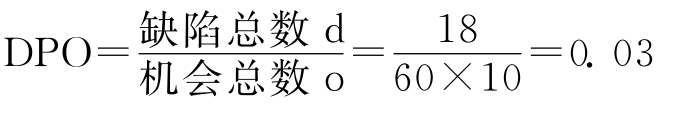
若把DPO乘以106就得每百万个机会的缺陷数（DPMO）为：

DPMO＝0．03×10⁶＝30000

5．流通合格率RTY。由于在生产线上每一工序都可能产生缺陷，一些缺陷可以通过返工修复成为合格的，因此最终的合格率不能反映中间工序返工所造成的损失。因此提出了流通合格率的概念。

流通合格率指每一工序合格率的乘积，用RTY表示，或者用YRT表示。例如，一个产品有8道工序，其中第二道工序的合格品率为0．955，第五、第八道的合格品率分别为0．97，0．944，另外五道工序无不合格品，则该产品的流通合格率为

RTY＝0．955×0．97×0．944＝87．4%

如图14－6所示。

图14－6　流通合格率计算体系图

二、6σ管理中常用的度量指标

6σ管理在“度量什么”和“怎样度量”上不同于传统的方法，它为提升组织的竞争力揭示出广泛的业绩改进空间。由于测量对象、测量方法和数据类型不同，在6σ管理中有若干种用于业绩度量的指标。

在6σ管理的度量中，常常用到下面的度量指标，它们是：CTQ（Critical to Quali－ty）——关键质量特性。它是指满足关键的客户要求或过程要求的产品、服务或过程特性；USL／LSL——规范上限／规范下限。这是客户可接受的产品、服务或过程特性的最大值和最小值；Taret——目标值。从客户的角度来看CTQ的理想值；FTY（First Time Yield）——首次产出率。这是指过程输出一次达到顾客规范要求的比率，也就是我们常说的一次提交合格率；RTY（Rolled Throughput Yield）——滚动产出率。这是构成过程的每个子过程的FTY之乘积。表明由这些子过程构成的大过程的一次提交合格率。RTY＝FTY₁′FTY₂′FTY_n，式中：FTY₁是各子过程的首次产出率，n是子过程的个数。

用FTY或RTY度量过程可以揭示由于不能一次达到顾客要求而造成的报废和返工返修以及由此而产生的质量、成本和生产周期的损失。这与我们所采用的产出率的度量方法是不尽相同的。在很多企业中，只要产品没有报废，在产出率上就不计损失。因此，掩盖了由于过程输出没有一次达到要求而造成的返修成本的增加和生产周期的延误。举例来说，某过程由4个生产环节构成。如图14－7所示。

图14－7　过程产出能力的两种不同的度量

该过程在步骤2和步骤4之后设有质控点。根据生产计划部门的安排，投料10件。经过步骤1和步骤2的加工后，再检验发现2个不合格品。1件须报废，另1件经返修处理后可继续加工，这样有9件进入了后续的加工过程。这9件产品经过步骤3和步骤4后又有1件报废，1件返修。整个加工结束后，有8件产品交付顾客。因此，生产计划部门的统计数据是：产出率＝80%。这个统计数据不能表明在这80%中，有一些是经过返修后交付的，这些返修活动增加了生产成本和生产周期。如果用RTY来度量的话，可以看出，步骤1和步骤2的FTY₁为8／10＝80%，步骤3和步骤4的FTY₂为7／9＝78%。如果投料100件的话，经过步骤1和步骤2，第一次就达到要求的是100×80%＝80件，这些一次就达到要求的合格品经过步骤3和步骤4后，一次就能达到要求的将是80件×78%＝62件。也就是100×80%×78%＝100×62．4%＝62．4件，而80%×78%＝62．4%正是我们说的FTY₁×FTY₂＝RTY。就这个例子来说，只有62%左右的产品（6件）是一次就达到加工要求的，而38%左右的产品需经返修或报废处理。

FTY＝99%是不是足够好？在很多人看来，这已经足够好了。FTY达到3．4ppm不过是种“理想”状态，实际上并不需要如此低的缺陷比率。但是，如果我们用RTY来度量的话，可以发现越是步骤多、越是技术含量高的过程，对FTY的要求就越高。从表14－2中可以看出，如果每个子过程的FTY都为99%，那么由50个子过程构成的大过程的RTY只有60．5%，也就是说将有40%的过程输出需经返工或报废处理。也许，经过返修处理后，过程的输出可以100%的交付顾客，用我们传统的产出率的统计方法，这个过程的产出率是100%。但事实上，这个过程中存在着质量、成本和周期的巨大损失，而这些损失是竞争力的损失。见表14－2。

表14－2　一些典型过程的FTY与RTY

我们还可以用下面一些度量指标衡量过程满足顾客要求的能力：

Defect——缺陷。这是指不满足CTQ规范的任何事件。

Unit——单位。这是指对其计数缺陷的物或事。如一件产品、一本账册、一米布、一吨煤、一次电话服务等。其具有边界或起始与终止点，是可观测和可计数的。

Opportunity——缺陷机会数。这是指可能产生缺陷之处的数量，如一块线路板有200个焊点就有200个缺陷机会；一张申请表有15个栏目就有15个缺陷机会等。

DPU（Defect Per Unit）——单位缺陷数。这是过程的“缺陷”数量与过程输出的“单位”数量比。平均每个单位上有多少缺陷。计算式为：

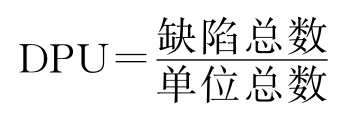
DPO（Defect Per Opportunity）——单位机会缺陷数。这是过程输出的“缺陷”的数量与过程输出的“缺陷机会数”之比。计算式为：

DPMO（Defect Per Million Opportunity）——百万缺陷机会缺陷数。这是过程输出的“缺陷”的数量与过程输出的“缺陷机会数”之比乘以1000000。计算式为：

DPMO＝DPO×1000000

假如一位顾客通过电话订购了4个汽车备件，希望5天内交付，那么，对交付过程来说，关键的顾客要求CTQ是及时交付订货，顾客要求的规范限USL是从接电话之日起5个工作日内，过程的缺陷是备件超过5天发出。对这次电话订货来说，有4个缺陷机会，因为每一个备件都可能延迟发出。如果该电话销售部门6个月内共收到电话订货20个，每个订货4件，其中未能准时发货的5件。那么，该过程的：

DPU＝5／20＝0．25——表示平均每次订货中有0．25件产品不能准时发出

DPO＝5／（20×4）＝0．0625——表示不能准时发货的产品占发出的所有产品的6．25%

DPMO＝0．0625×1000000＝62500——表示如果发出1000000个产品的话，将有62500个产品不能准时发出。

对很多产品或服务过程来说，满足顾客要求的特性不止一个，引起不合格的缺陷不止一处。采用DPU或DPMO可以更准确地度量过程满足顾客要求的能力，给我们更多关于过程缺陷的信息。

如果度量条件允许的话，应尽量使用连续型数据并根据这些测量数据与顾客要求目标值的偏离程度作为过程满足顾客要求的能力的度量指标：

平均差X（上补横杠），是描述计量值质量特性分布中心位置的样本统计量。

标准差S，是描述计量值质量特性分布分散程度的样本统计量。标准差越大，分布越分散。标准差越小，分布越集中。

σ水平Z，是描述过程满足客户要求的能力的参数，描述了过程的输出与客户要求目标值的接近程度。

通过对过程输出的准确测量，可以获得连续型的测量数据，根据这些数据，可以计算出过程输出的平均值和标准差，用这两个参数可以计算过程的σ水平，表示过程满足顾客要求目标值的能力。计算公式为：

Z＝min（Z_pu，Z_p1）

注：式中min表示取Z_pu和Z_pl两者中小的。

比如：某顾客对某产品的性能十分关注，要求该性能为Y＝10±0．01。供应商A提供的10个产品的测量数据为：10．009、10．005、9．992、9．999、10．008、10．007、9．997、9．999、10．009、9．995。供应商B提供的10个产品的测量数据为：10．002、10．003、9．998、9．999、10．001、10．003、9．999、9．999、10．002、9．998。那么，谁更能满足顾客要求呢？根据这些数据，我们可以分别计算出它们的平均值和标准差。供应商A的平均值为10．002，标准差为0．00632。供应商B的平均值为10．0003，标准差为0．00211。将这些数据以及顾客要求代入上面的Z计算公式，可得供应商A的σ水平为1．27，供应商B的σ水平为4．60。也就是说，供应商B的产品更接近于顾客要求的目标值（此例中，顾客要求的目标值为10），因此供应商B满足顾客要求的能力远高于供应商A。

又比如：某顾客采取零库存管理，要求供应商A提供产品的交付期为下订单后第30天，早于30天的话，供应商A自己负责保管，每天需付额外保管费，但最多可保管7天。下面是供应商A的10批产品交付时间的统计数据：29、27、25、24、29、26、23、25、30、24（天）。那么，该供应商交付过程的σ水平是多少呢？根据交付时间的统计数据，可以计算出该过程的平均值等于26．2，标准差S＝2．44。该过程的规范限LSL＝23。将这些数据代入公式，可得Z＝（26．2－23）／2．44＝1．37。也就是说该过程的σ水平仅为1．37。观察这些交付时间的统计数据，虽然没有早于23天或迟于30天的。但是，因为它们相对于顾客要求的目标值来说比较分散，因此过程的σ水平并不高。σ水平低意味着过程满足顾客要求的能力低，意味着质量、成本和周期的损失。

上面介绍了用于业绩度量的三大类指标：基于合格／不合格（计数型数据）的FTY／RTY度量指标；基于缺陷数据（计点型数据）的DPU／DPMO度量指标；基于平均值／标准差（连续型数据）的Z（σ水平）。它们基本覆盖了对产品、服务、商务、管理等所有类型过程的度量。为了将这三类度量指标统一起来，在6σ管理中常常将FTY／RTY，或DPU／DPMO折算为近似的Z（σ水平）。在折算过程中采用了将FTY／RTY或DPU／DPMO转换为标准正态分布中对应的概率，并根据概率分布找出对应的Z。6σ管理中常用的Z换算表如图14－8所示。

图14－8　2FTY／RTY／DPU／DPMO与σ水平的估算

三、6σ管理与业绩度量

σ在统计学中表示数据的分散程度，在6σ管理中，一般常用下面的计算公式表示σ的大小：

式中：X_i为样本观测值；X为样本平均值；n为样本容量。

如果有两组数据，它们分别是1、2、3、4、5和3、3、3、3、3，虽然它们的平均值都是3，但是它们的分散程度是不一样的（如图14－9所示）。如果我们用s来描述这两组数据的分散程度的话，第一组数据的s为1．58，而第二组数据的s为0。假如，把数据上的这些差异与企业的经营业绩联系起来，这个差异就有了特殊的意义。

假如顾客要求的产品性能指标是3±2（mm），如果第一组数据是供应商A所提供的产品性能的测量值，第二组数据是供应商B所提供的产品性能的测量值。显然，在同样的价格和交付期下，顾客愿意购买B的产品。因为，B的产品每一件都与顾客要求的目标值或理想状态最接近。它们与顾客要求的目标值之间的偏差最小。

假如顾客要求的产品交付时间是3天。如果第一组数据和第二组数据分别是供应商A和B每批产品交付时间的统计值，显然，顾客愿意购买B的产品。因为，B每批产品的交付时间与顾客要求最接近。尽管两个供应商平均交付时间是一样的，但顾客的评判，不是按平均值，而是按实际状态进行的。

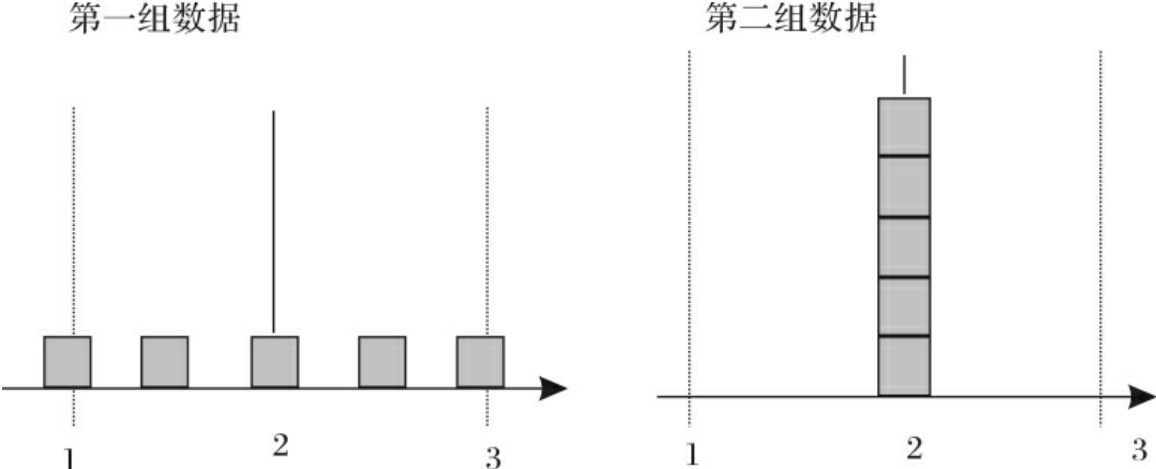
图14－9　两组分散程度不同的数据

假如顾客要求每批产品交付数量是3件。如果第一组数据和第二组数据分别是供应商A和B每批产品交付数量的统计值，显然，供应商B向顾客供货的能力要大于A。因为，供应商B每批都准确地达到了顾客交付数量的要求，而供应商A在交付期内不是由于各种原因达不到交付数量的要求，使顾客不满意；就是多生产了产品，增加了库存，积压了资金。

假如这些数据代表了服务响应时间、顾客满意程度、产品开发周期等等，这些数据与顾客要求的离散程度以及与竞争对手的差异，就有了管理上的特殊意义。

6σ管理特别强调度量的作用，强调用顾客满意的方式，用提高竞争力和追求卓越的方法度量我们的业绩。这点与我们传统的管理模式与方法是根本不同的。让我们来看一看，在“度量什么”和“怎样度量”上，6σ管理与我们传统的做法有什么不同。

首先，在“度量什么”上，6σ提供了广泛的业绩度量“视角”，它强调按照顾客的需求和企业发展重点度量组织业绩的各个方面。比如，交付期、交付状态、产品质量、服务特性、成本、库存、顾客满意、员工满意、管理活动等等。通过对组织业绩的广泛度量，寻求组织业绩突破和改进的空间。

再则，在“怎样度量”上，6σ管理提供了“追求卓越”的度量方法。传统上，我们的度量仅限于“符合性”上。举例来说，对照规范检查产品质量，把符合规范的记为合格品，对合格品来说，一般不再关心其符合顾客要求的程度。例如，某工序生产了A、B、C三个零件，A的测量值接近顾客要求的目标值，而B接近于规范下限，C则超过了规范下限（如图14－10所示）。我们把控制与改进的注意力集中在C上。尽管A产品的质量接近理想状态，而B产品几乎超差，但在传统的度量方法下，它们的质量表现是一样的，都视为合格品。但正是这种度量方法忽略掉的差异，在竞争力方面带来了不可忽略的差异。6σ管理重视符合顾客要求程度方面的差异，并通过采用揭示这些差异的度量方法，展示业绩改进的空间。

在6σ管理中，通常使用σ水平Z作为满足顾客要求程度的业绩度量。Z有几种表达形式：最简单的一种是用测量数据的标准差s与顾客要求的上限（USL）和下限（LSL）的关系来表达，其公式为：

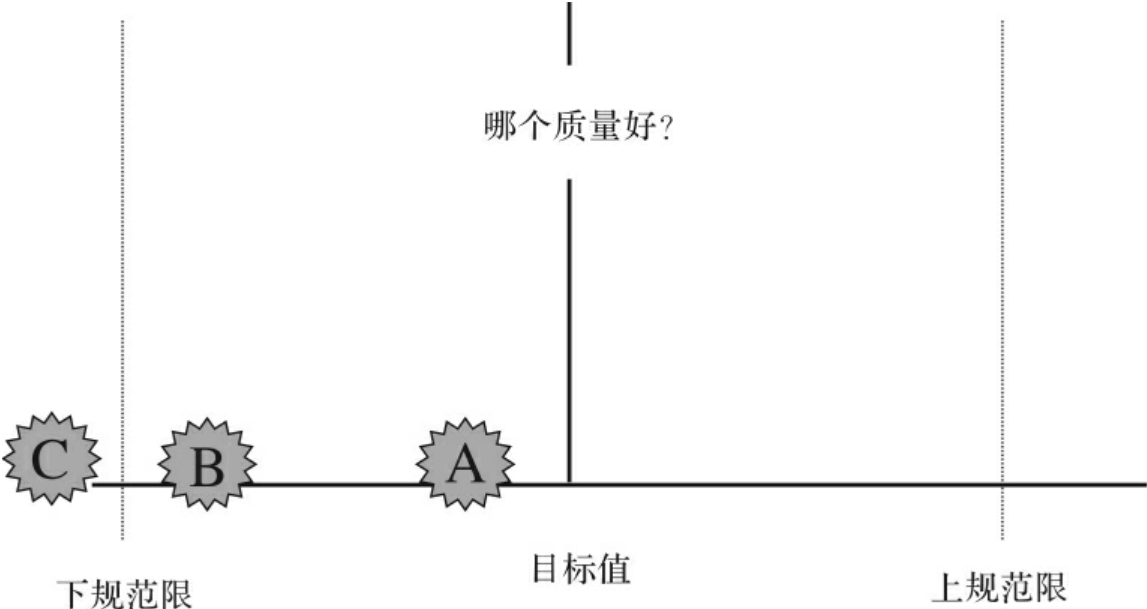
图14－10　与传统度量方式的比较

达到6σ水平是指Z等于6。如果用我们熟悉的正态分布来解释的话，也就是说过程的波动非常小，集中在目标值附近，它们满足顾客要求的能力很强。而3σ水平则波动较大，其满足顾客要求的能力远不如6σ水平。如图14－11、图14－12所示。

图14－11　波动3σ水平与6σ水平的比较

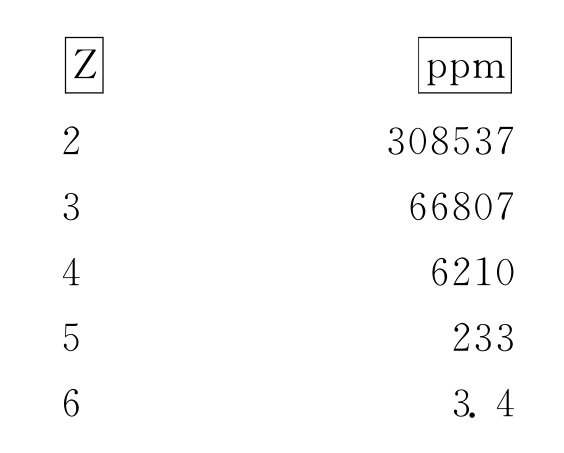
Z还有另一种表达形式：用百万分之缺陷率（ppm）来表示。一个服从正态分布的过程，其超出规范限的缺陷百分比与σ水平是一一对应的。如图14－13所示。

根据这个规律，可以通过测量缺陷的比率，估算过程的σ水平Z，并以此考察过程满足顾客要求的能力。通常，6σ水平所代表的过程缺陷率为3．4ppm，而3σ水平的缺陷率为66807ppm。

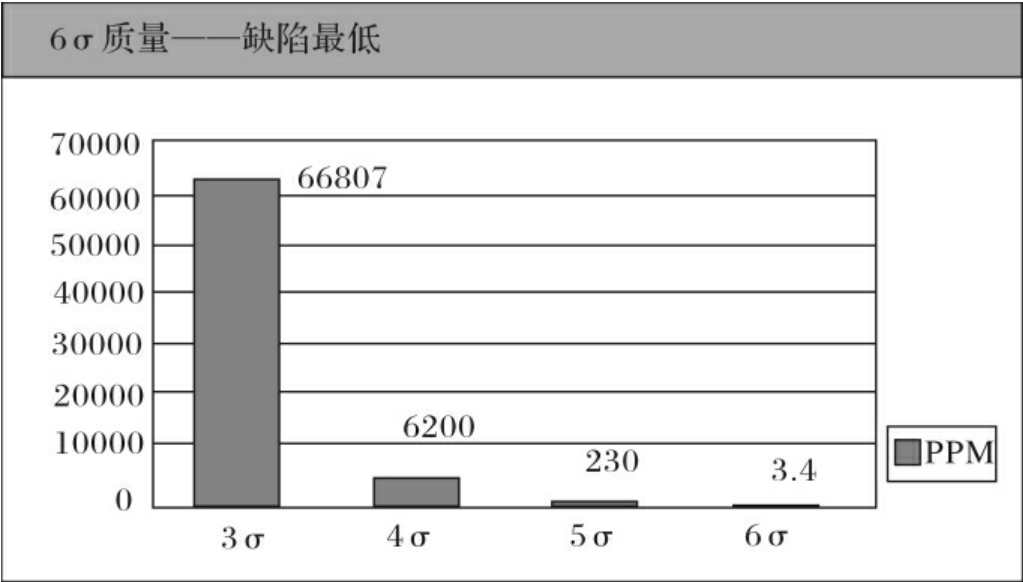
图14－12　波动3σ水平与6σ水平的比较

图14－13　缺陷率与σ水平的估算

用顾客满意的方式，用提高竞争力和追求卓越的方法度量业绩的方方面面，是6σ管理的基础。只有解决了“度量什么”和“怎样度量”的问题，才能发现我们在竞争力上的差距和改进空间。这是实施6σ管理首先要解决的问题。

（分布中心漂移±1．5σ）