工期优化费用优化资源优化口诀

第四节　网络计划的优化

网络计划的优化就是利用时差不断改善网络计划的最初方案，在满足既定目标的条件下，按某一衡量指标来寻求最优方案。

例如：在人力、材料、设备和资金等资源有限条件下，寻求工期最短；在工期规定的条件下，寻求投入的人力、材料、设备和资金等资源的最小数量；在最短期限完成计划的条件下，寻求成本最低等。

对网络计划的调整优化，应综合考虑进度、成本费用和质量，以实现项目的目标，网络计划的优化一般有工期优化、资源配置优化和工期—成本优化方法。

一、工期优化

采用工期优化主要是为了满足项目计划按规定的时间或提前完成而进行的调整，其工期为主要的优化目标，这时的约束条件又分为两种。

(一)资源不受限制的工期优化

由于资源不受限制，可采取的补救方法就有很多，例如增加人工，选用新技术和更多的设备等资源，以实现工期缩短满足要求为目的，但这样会增加资源的消耗即增加成本，同时在采用更多的资源时，还应考虑该项目是否能提供足够的工作面来加快工作的进展。

(二)资源有限的工期优化

由于资源受到限制，一般要求在合理使用和安排有限资源的条件下，满足规定的工期或使延长的工期时间最短，通常是调整工作的顺序解决资源供给与需求的矛盾。

1.基本原理

假定I，J，K为某个项目的三个工作，网络的时间参数和资源需要量如表6-3所示，其资源视作起重机且这三个工作只能提供两台起重机。

表6-3

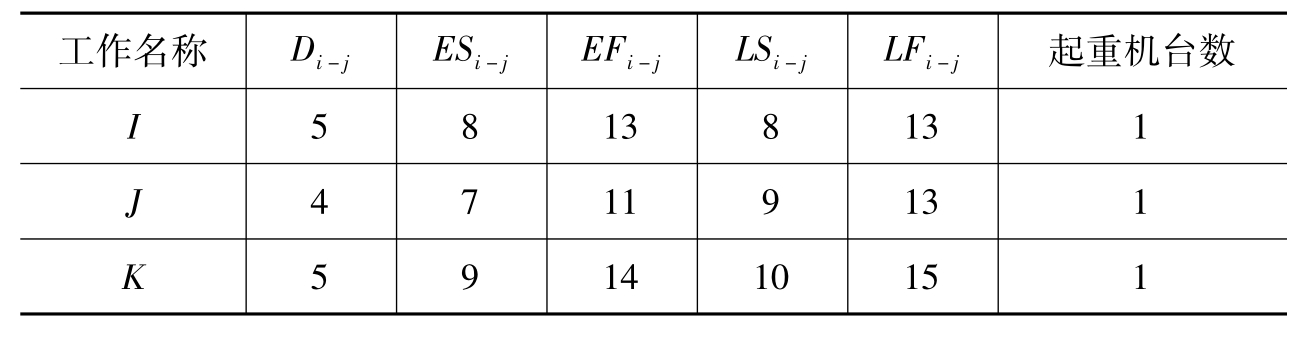
按网络图的时间参数绘制横道图如图6-17所示。

从图6-17中我们可以看出，如果以网络时间参数的最早可能时间作参考，在工作第9天到第11天，三项工作需同时进行，那么同时需要起重机共3台，而这三项工作的资源只有两台，这时需停下一项工作延长一定的工期，才能满足条件，那么停下哪一项工作的延长时间最短呢?

按各工作的网络时间参数计算如下：

K放在J后面，Δt_jk=EF_j－LS_k=11－10=1天

J放在K后面，Δt_kj=EF_k－LS_j=14－9=5天

I放在J后面，Δt_ji=EF_j－LS_i=11－8=3天

图6-17

J放在I后面，Δt_ij=EF_i－LS_j=13－9=4天

I放在K后面，Δt_ki=EF_k－LS_i=14－8=5天

K放在I后面，Δt_ik=EF_i－LS_k=13－10=3天

则通过计算可知将工作K排在工作J后面可使工期延长最短时间Δt=1天，即找出一个最迟开始的工作排在最早完成工作之后，能够使得工期拖延最短。

2.优化步骤

(1)将一般网络计划绘制成带有时间坐标的网络图及资源动态曲线。

带有时间坐标的网络图即时标网络图，即带有工作日或日历天的进度计划，按照各工作的先后顺序和相互关系及按照最早可能开始和最早可能结束的时间绘制各工作的箭杆和事件，工作箭杆长度与时间坐标是一致的。

从该时标网络图可以找出关键线路和非关键线路，可以确定每个时间是否能满足资源条件的限制。

(2)按从左向右的顺序，计算发生资源冲突的时段内工作安排的顺序，即确定minΔt。

(3)按调整后的网络计算时间参数，重新绘制资源动态曲线。

(4)将延长工期和增加资源损失进行比较，选用最优方案。

3.计算实例

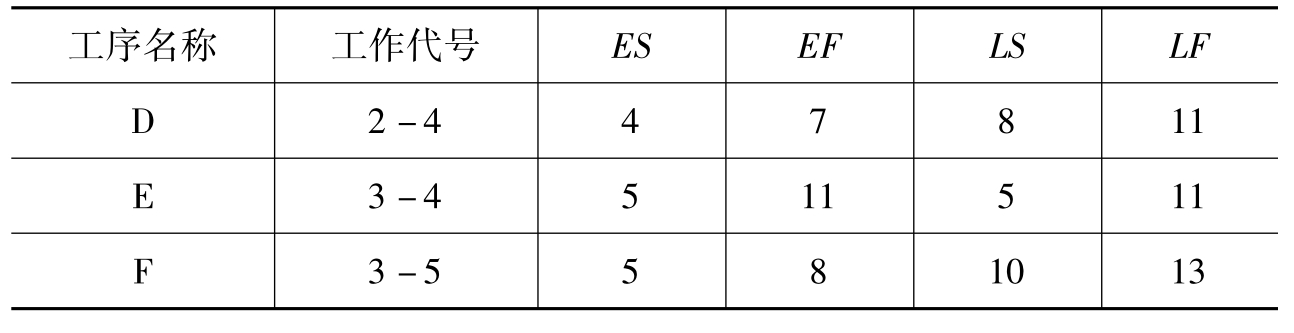
例2：某项目网络计划如图6-18，时间参数见表6-4，已知资源限量为每日工人数最多为40人，要求调整计划使在资源限制条件下工期最短。

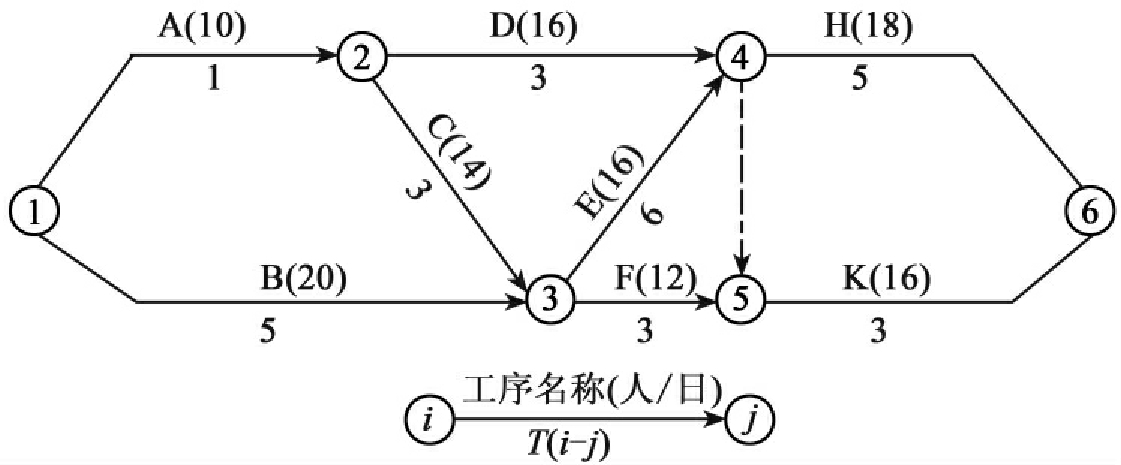
图6-18

表6-4　网络图时间参数计算结果

解：(1)画出时标网络图及相应的资源动态曲线，见图6-19。

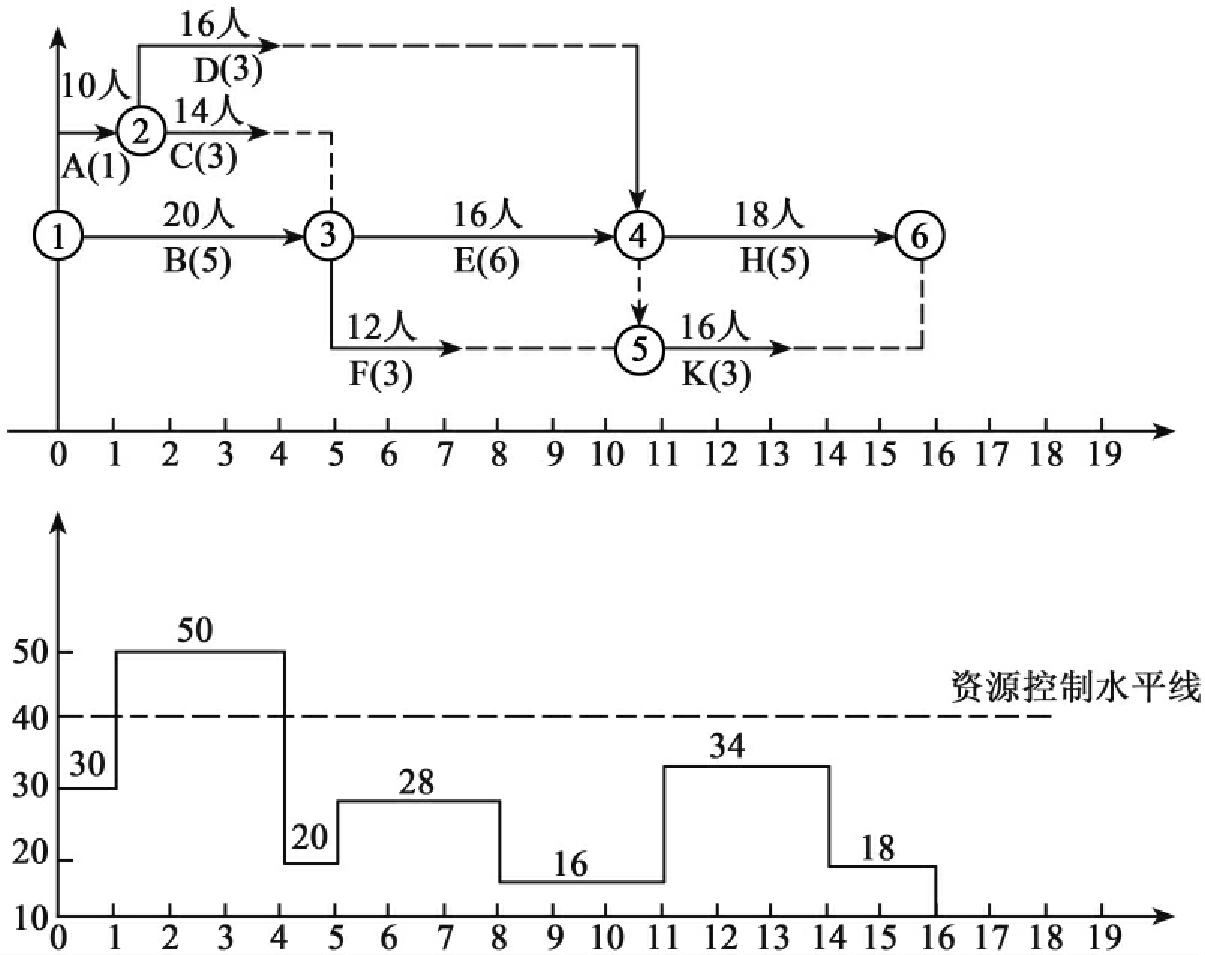
图6-19

(2)从左向右检查资源动态曲线，我们发现发生资源冲突的工作有B、C、D三项，从网络时间参数计算结果我们可以看出，最小的最早可能结束的工作是工作C、D，EF=4，最大的最迟必须开始时间为工作D，LS=8天，所以将工作D放在工作C之后。

调整网络计划及资源动态曲线，如图6-20所示。

(3)再检查图6-20时标网络和资源动态曲线图时，发现工作D、E、F在时段5～7天内资源发生冲突。第一次调整后的网络时间参数如表6-5。

从网络时间参数计算结果可知，EF最小的工作为工作D，EF=7天，LS最大的工作为工作F，LS=10，将工作F放在工作D之后。

调整网络计划及资源动态曲线，如图6-21所示。

(4)经过调整后的网络计划，各段资源需要量均不超过资源最大限量。

最高使用人数为36人/天，总工期仍为16天。

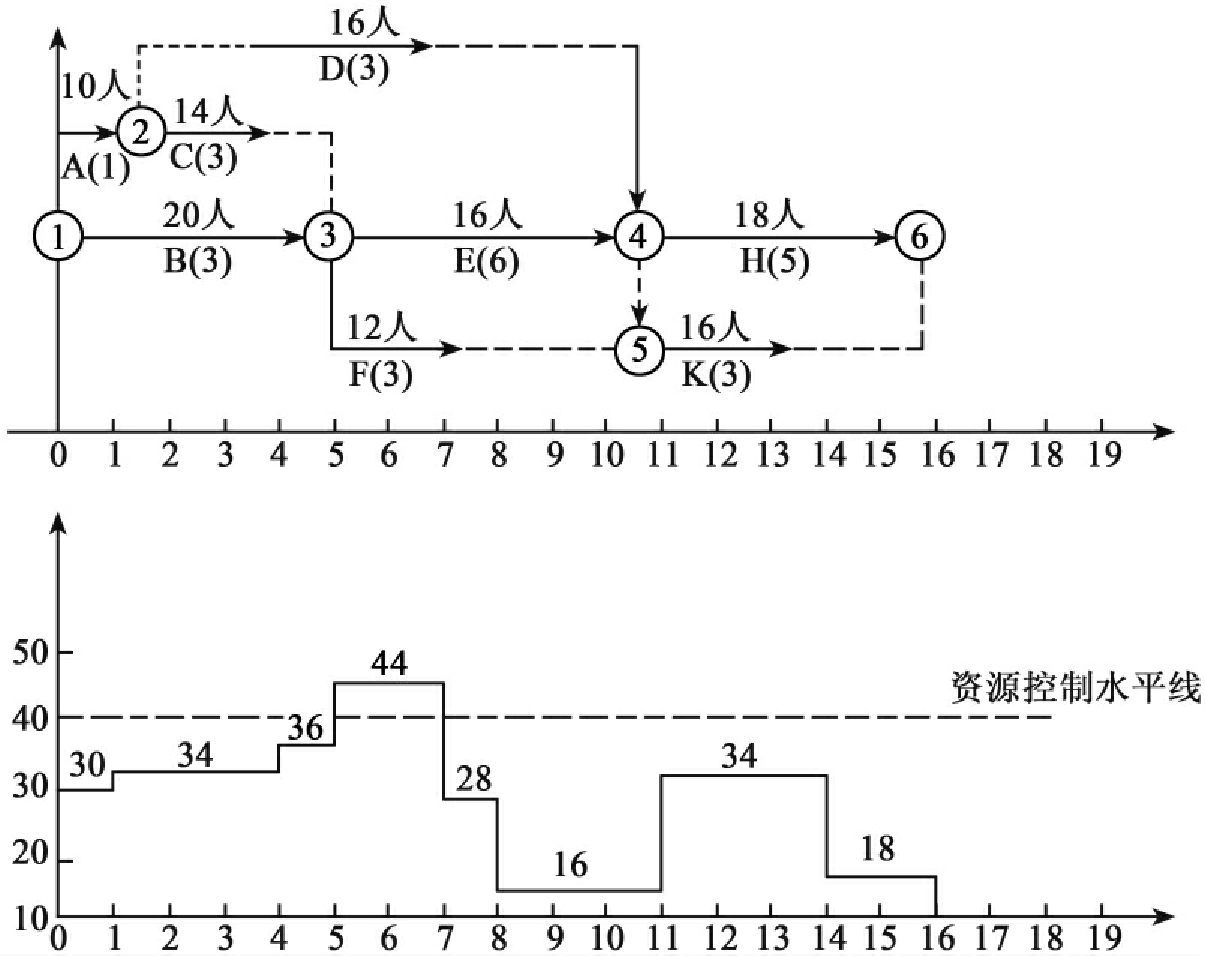
图6-20

表6-5

二、资源配置优化

资源配置优化是通过改变工作的开始时间，使资源按时间的分配达到均衡合理的优化目标。

(一)衡量资源消耗均衡性的指标

1.不均衡系数K

根据资源需要量动态曲线计算不均衡系数K。

图6-21

显然，在不同计划方案比较中，资源需要量不均衡系数越小，说明其资源配置的均衡性越好。

2.极差值ΔR

根据资源需要量动态曲线，每天计划需要量与每天平均需要量之差的最大绝对值。

式中，R_t：第t天的资源需要量

　　　T：该项目计划完成的时间

同样，其极差值越小，资源配置的均衡性就越好。

3.均方差值σ²

根据资源需要量动态曲线，每天计划需要量与每天平均需要量之差的平方和的平均值。

同样，均方差值越小，资源配置的均衡性就越好。

要使均方值最小，即使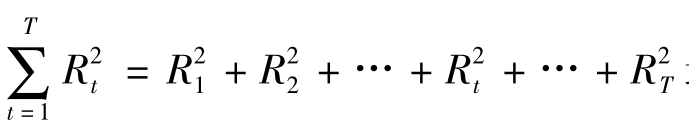最小。

这三个指标从不同角度进行相同目标的优化，其解法也不相同。本书只介绍均方差值最小的近似解法。

(二)优化方法

1.根据网络计划的最早可能开始时间绘制时标网络和资源需要量动态曲线

使计划的总持续时间不变，在调节资源均衡的过程中，一般不调节关键线路上的工作。

2.按事件最早开始的后先顺序，从右向左进行调整

假定工作i－j为非关键工作，在第k天开始，到第l天结束，且j点为最右的一个事件，那么工作i－j向右移动一天，则第k天资源需要量将减少单位时间资源需要量r_i－j，而第l+1天资源需要量将增加单位资源需要量r_i－j，即

R'_k+1=R_k－r_i－j

R'_l+1=R_l+1+r_i－j

工作i－j向右移一天后，均方差值的变化即R²₁+R²₂+…+ R²_t+…+R²_T的变化值等于

Δσ²=［(R_l+1+r_i－j)²－R²_l+1］－［R²_k－(R_k－r_i－j)²］

化简后：

Δσ²=2r_i－j［R_l+1－(R_k－r_i－j)］

若要知道Δσ²的变化，只需讨论［R_l+1－(R_k－r_i－j)］的变化

当R_l+1－(R_k－r_i－j)＜0时，即意味着工作i－j向右移一天的均方差值变小，那么工作i－j可以向右移一天，如果再能移动一天，那么就再右移一天，直到不能移动为止。

当R_l+1－(R_k－r_i－j)=0时，即意味着工作i－j向右移一天的均方差值没有变化，即资源的均衡性没有改善，当然工作i－j也可以向右移动。

当R_l+1－(R_k－r_i－j)＞0时，即意味着工作i－j向右移一天的均方差值变大，那么工作i－j不能向右移一天，那么就考虑向右移2天(在总时差许可的范围内)继而可考虑向右移3天(在总时差许可的范围内)，直到不能移动为止。

3.不断调整、循环，直到使均方差值最小

注意资源配置均衡优化时，要按事件最早可能开始时间的后先顺序对非关键工作从右向左利用时差进行调整。当某事件前有几项非关键工作时，按局部时差大小的先后顺序调整，即局部时差大的工作先调整，局部时差小的工作后调整。

(三)计算实例

例3：将图6-22进行工期规定，资源均衡优化，假设所有的工作都需要同一种资源S=1。

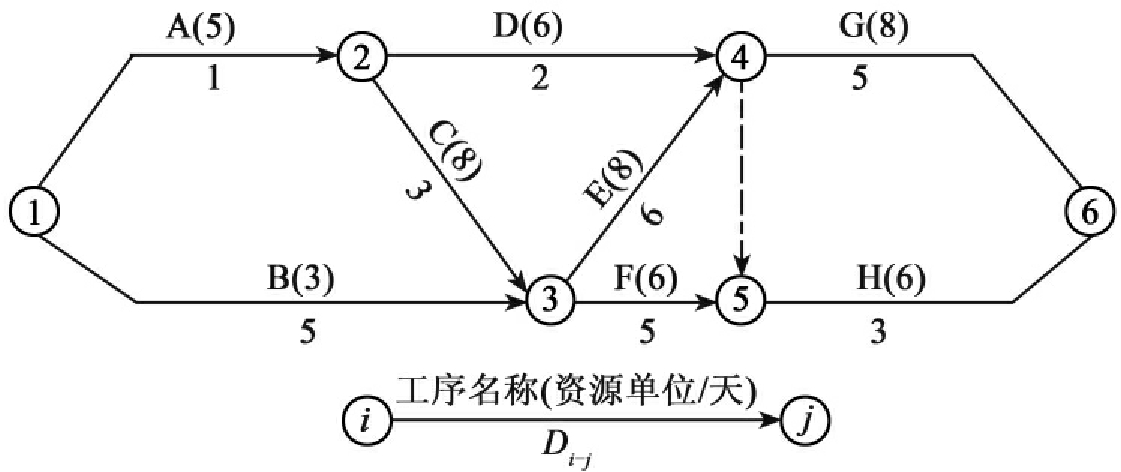
图6-22

解：(1)计算该网络计划的时间参数见表6-6。

确定该网络计划的关键线路为①－③－④－⑥，工期T=16天。

(2)画出时标网络图和资源动态曲线如图6-23所示。

可知，原资源需要量平方和为

表6-6　网络计划的时间参数

图6-23

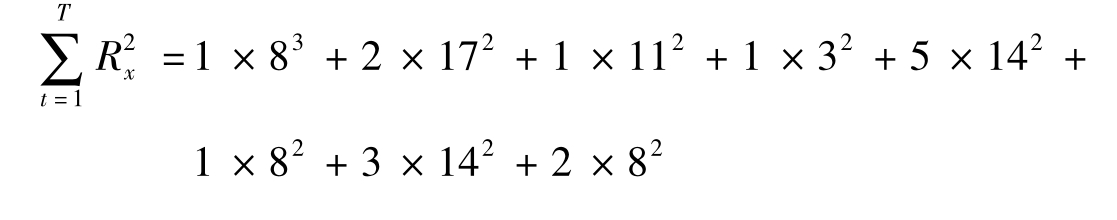
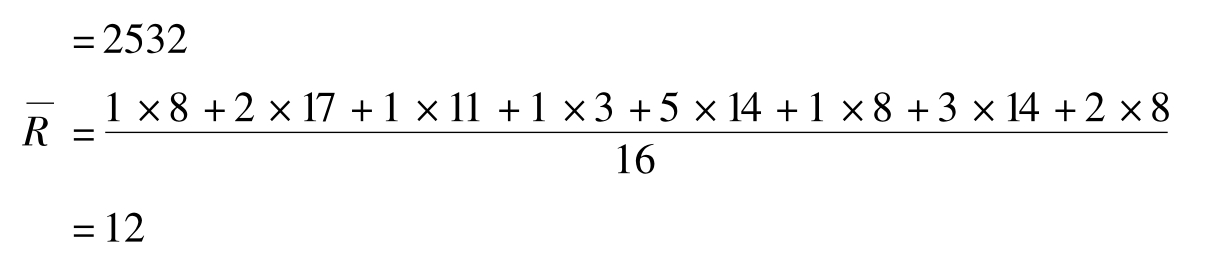
第一步，找出网络图中最右边的事件，调整非关键工作⑤－⑥。

R_l+1－R_k'≤0即R₁₅－R'₁₂=8－(14－6)=0

则工作⑤－⑥可右移一天。

再考虑工作⑤－⑥是否可以再右移一天：

R_l+1－R'_k≤0即R₁₆－R'₁₃=8－(14－6)=0

则工作⑤－⑥可再右移一天，即工作⑤－⑥可以共向右移动2天(该工作的总时差TF=2天)，如图6-24所示。

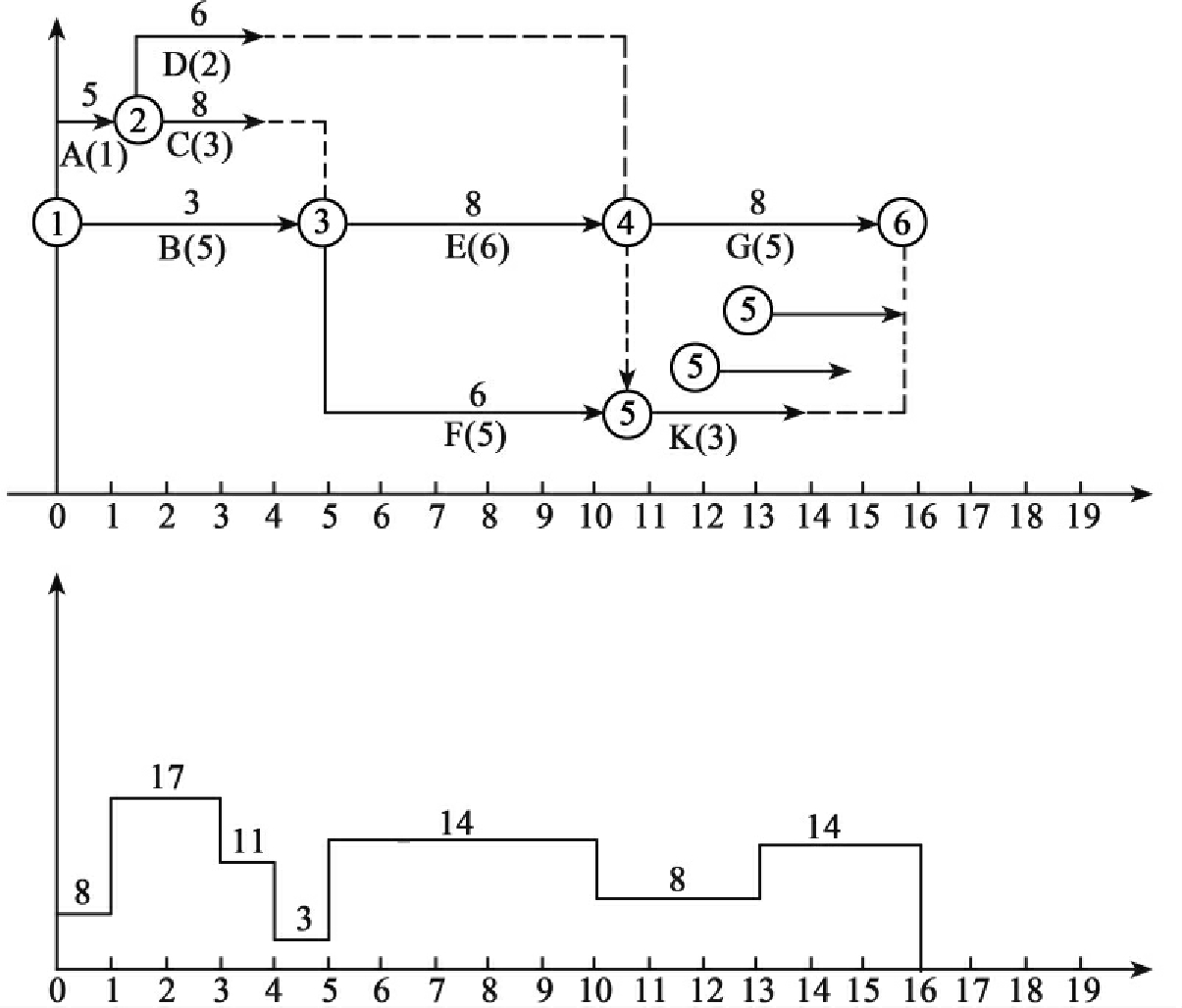
图6-24

第二步，从右向左顺序，找出事件5，调整非关键工作③－⑤。

R_l+1－R'_k≤0即R₁₁－R'₆=8－(14－6)=0

则工作③－⑤可向右移一天。

再考虑工作③－⑤是否可以再向右移一天。

R_l+1－R'_k≤0即R₁₂－R'₁=8－(14－6)=0

则工作③－⑤可再向右移一天。

再考虑工作③－⑤是否还可以再右移一天：

R_l+1－R'_k≤0即R₁₃－R'₈=8－(14－6)=0

则工作③－⑤可以再移一天，即工作③－⑤可以向右共移3天(该工作调整后的总时差为TF=1+2=3天)，如图6-25所示。

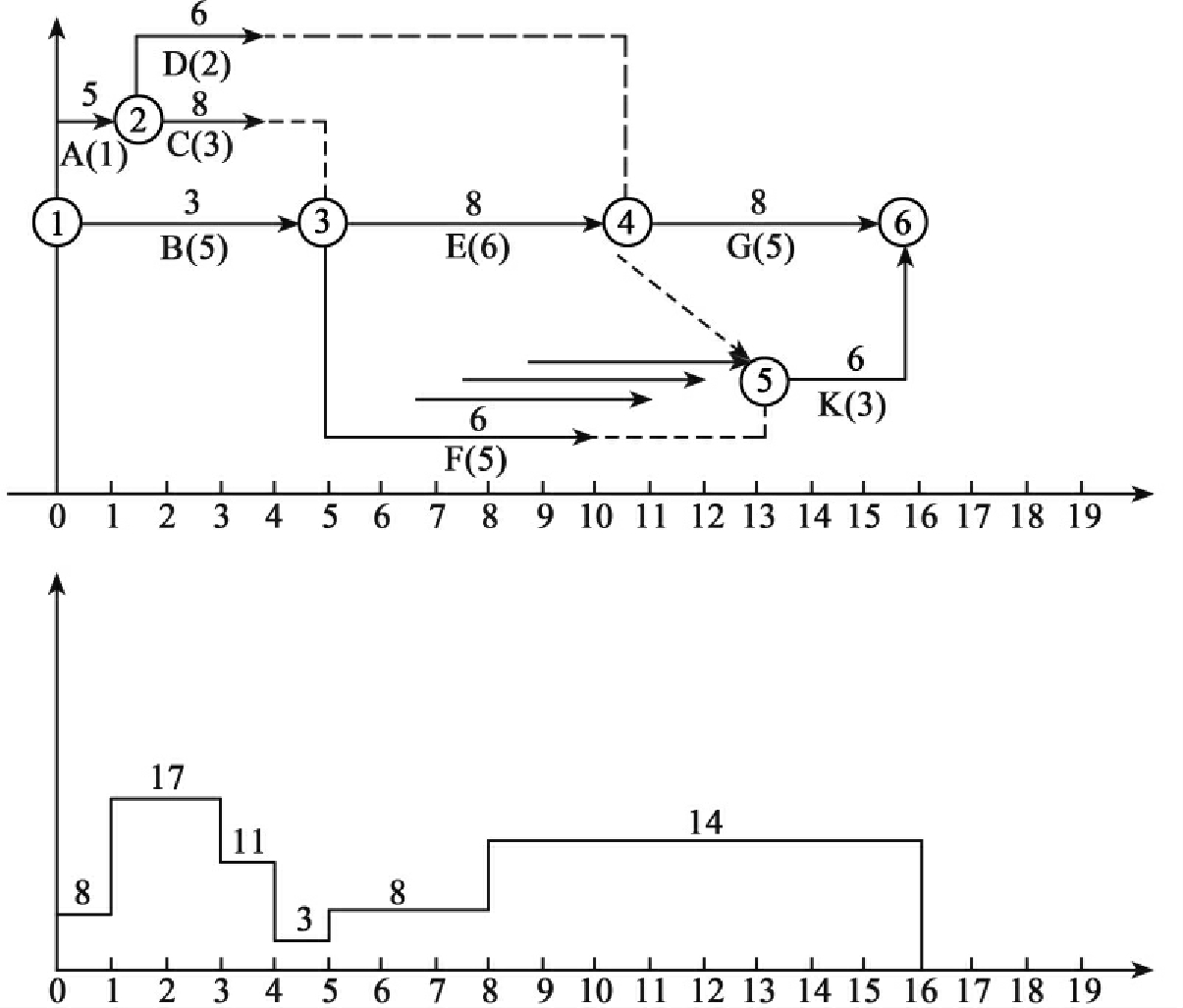
图6-25

第三步，从右向左的顺序，找出事件的调整非关键工作②－④。

计算　　　　　　　R_l+1－R'_k≤0

即

　　　　　　　　R₄－R'₇=11－11=0

则工作②－④可向右移一天。

同理　　　　　　　　R₅－R'₃=3－11=－9＜0

　　　　　　　　　　R₆－R'₄=8－17=－9＜0

则工作②－④可再向右移2天。

R₇－R'₅=8－3=5＞0

则工作②－④不能再向右移动，即工作②－④一共可向右移动1+2=3天。

经检验，本例题所有工序不能再向右移动，最后调整后的网络计划及资源动态曲线见图6-26所示。

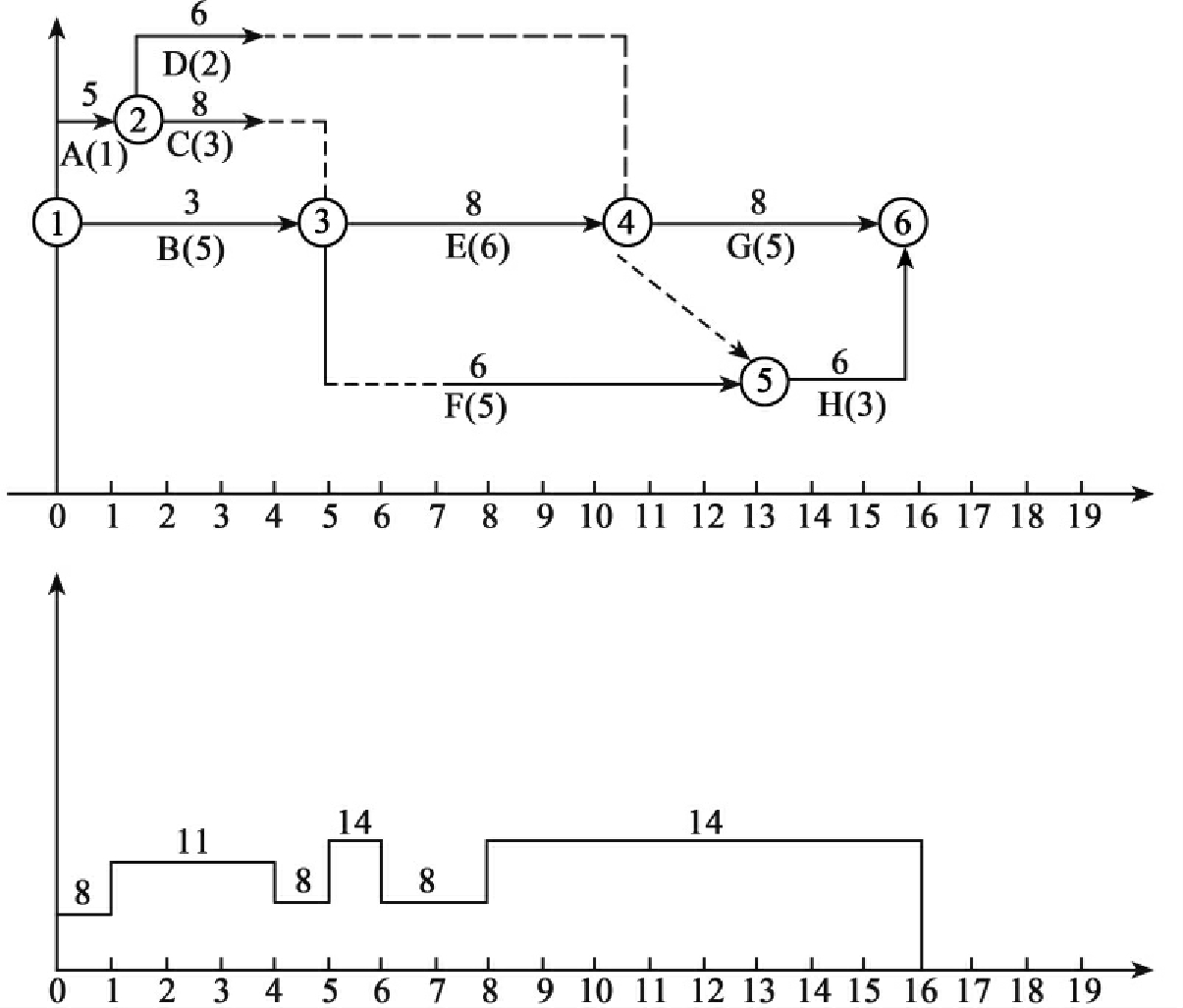
图6-26

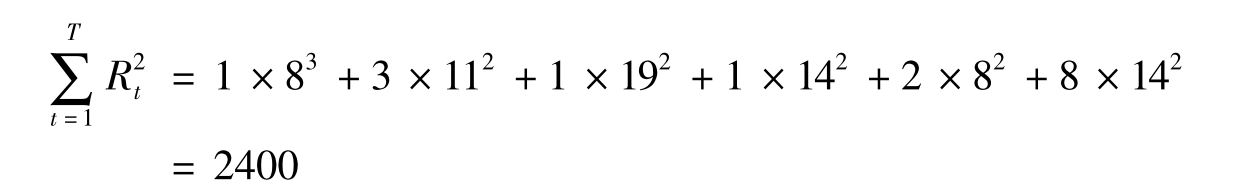
则　　　　　σ^调2=2400/16+12²=6

优化后的均方差值σ²=6＜14.25，即资源的均衡性得到了改善。

三、工期—成本优化

项目的优化总目标是成本低，工期短，质量优，其中工期与成本是相互联系和相互制约的，要加快进度，缩短工期，必须增加资源，必然导致成本增加。

(一)概念

1.成本

成本一般由直接费用和间接费用组成，在正常的条件下，加快进度，会增加直接费用，减少间接费用，而由于拖延进度，会降低直接费用，增加间接费用。

一般直接费用与工期成反比，且随着工期的缩短而更快地增加，间接费用与工期成正比，如图6-27所示。

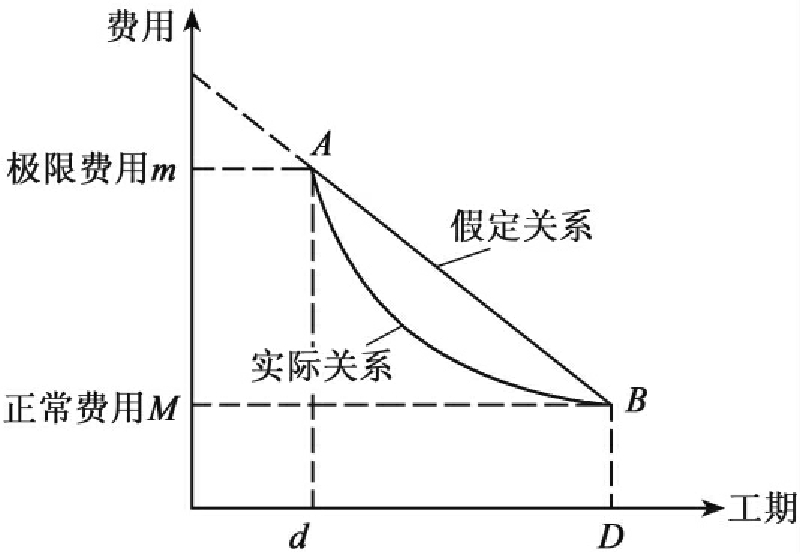
图6-27

2.优化目的

寻求直接费用与间接费用总和(成本)最低的工期T_R，以及与此相适应的网络计划中各工作的进度安排。

在规定的工期条件下，寻求与此相适应的最低成本以及相应的网络计划中各工作的进度安排。

3.工作的持续时间—费用曲线(即工作的直接费用率)

这种费用曲线一般用于连续型工作，即介于正常持续时间与最短持续时间之间任意时间的费用可用数学方法推算出来的工作，则对于连续性时间—费用关系的任意工作i－j有

其中，C_i－j：工作i－j赶工单位时间增加的直接费用，即称工作的直接费用率

m_i－j和d_i－j：采取措施后工作i－j可能增加的直接费用和最短持续时间

M_i－j和D_i－j：正常条件下工作i－j的直接费用和持续时间

(二)基本原理

1.工期—成本优化，主要是求出不同工期下的最小费用总和

2.因为关键线路是决定工期长短的依据，缩短工期，首先必须缩短关键工作的持续时间

3.采用“最低费用加快法”缩短工期，即缩短关键工作中直接费用率最小的持续时间

4.“最低费用加快法”具体做法

(1)关键线路只有一条时，压缩费用率最小的工作持续时间。

(2)关键线路有两条或两条以上时。

①每条线路都要压缩相同的持续时间Δt时，工期才能缩短压缩Δt。

②压缩工作的持续时间时，找出直接费用率总和∑C_i－j最小的工作组合，称为“最小切割”。

(3)关键线路上各工作持续时间压缩之和不能大于非关键线路的总时差，否则非关键线路就会变成关键线路。

(三)计算实例

例4：某工程的网络计划如图6-28所示，合同工期为20周，试用工期—成本优化的方法使该计划的工期满足合同要求。

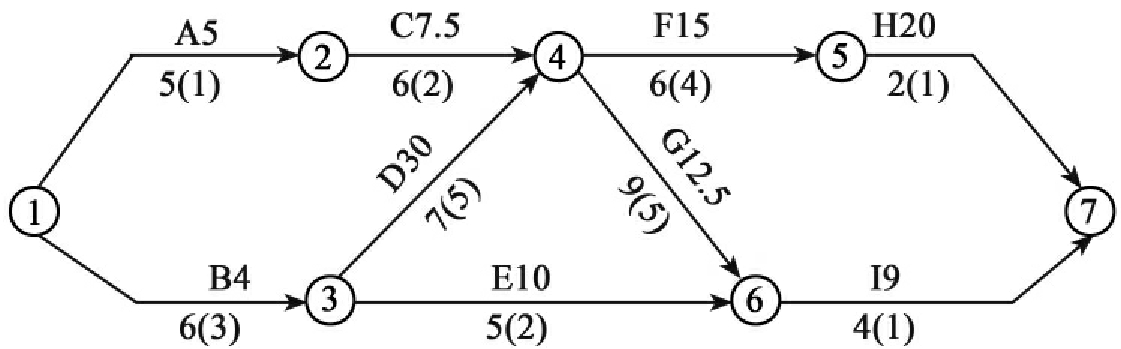
图6-28

解：按正常持续时间计算网络的时间参数如表6-7。

表6-7　按正常持续时间计算网络的时间参数

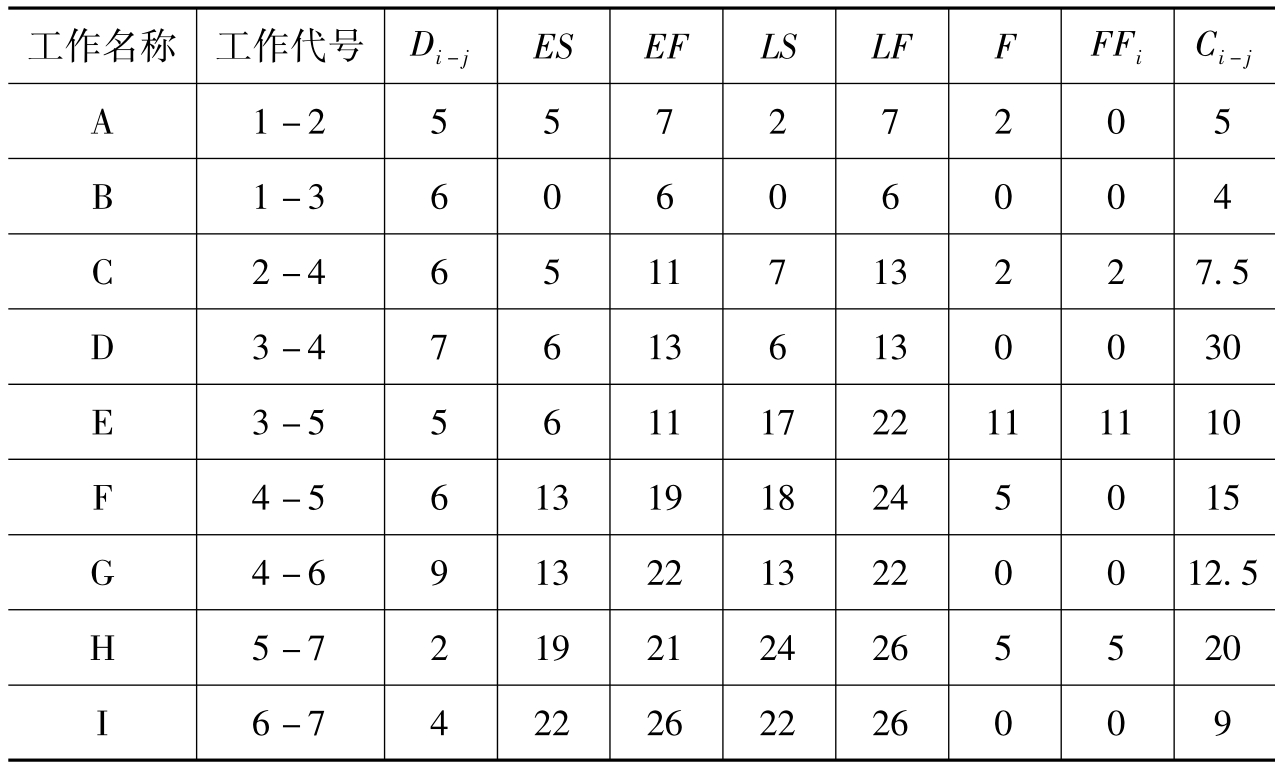
根据计算结果，确定网络的关键线路为①－③－④－⑥－⑦，工期T=26周，对该网络计划进行优化。

第一次压缩关键工作的持续时间：

(1)确定原关键线路，找出关键工作即工作B，D，G，I

(2)找出关键工作直接费用率最小的工作为压缩对象

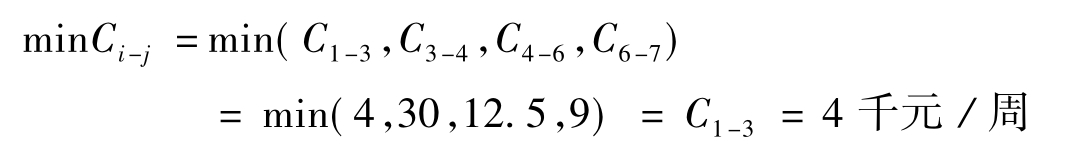
则选择工作①－③为压缩对象。

(3)确定工作①－③的压缩时间

假设工作①－③压缩时间为6－3=3周而工作①－②和工作②－④的总时差为2周，所以工作①－③压缩时间，Δt₁=2周，使得d_1－3=4周。

在网络图中，还可以看出，关键工作①－③压缩后，工作①－③的持续时间应满足

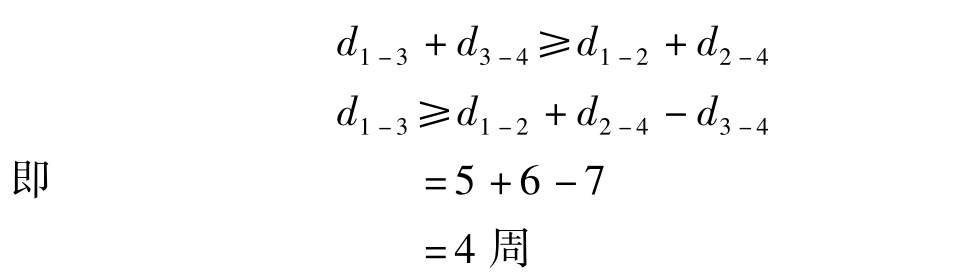
(4)压缩后工期T₁=T_0－2=26－2=24周

增加直接费用ΔC₁=2×4=8千元

第一次压缩后网络计划的时间参数变化见表6-8。

表6-8

第二次压缩关键工作的持续时间：

(1)确定关键线路，即①－②－④－⑥－⑦和①－③－④－⑥－⑦，找出关键线路关键工作为A、C、G、I和B、D、G、I。

(2)用最小切割为压缩对象，见图6-29。

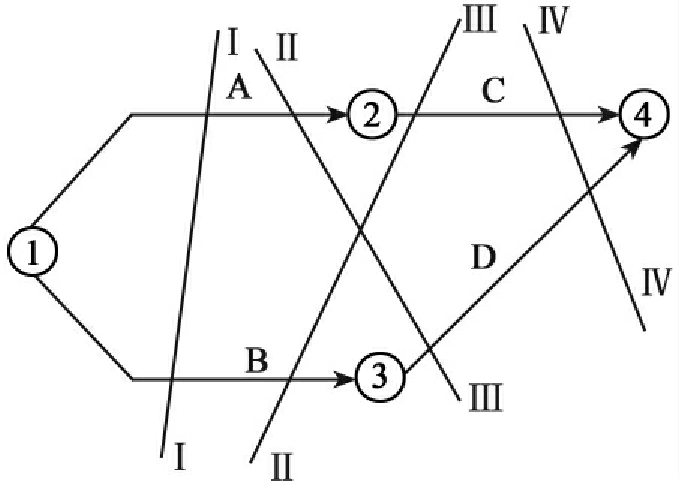
图6-29

切割Ⅰ－Ⅰ，工作①－②和①－③，∑C_i－j=4+5=9千元/周

　　Ⅱ－Ⅱ，工作①－②和③－④，∑C_i－j=5+30=35千元/周

　　Ⅲ－Ⅲ，工作②－④和①－③，∑C_i－j=4+7.5=11.5千元/周

　　Ⅳ－Ⅳ，工作②－④和③－④，∑C_i－j=7.5+30=37.5千元/周

找出关键线路上最小关键工作或关键工作的组合为压缩对象，即

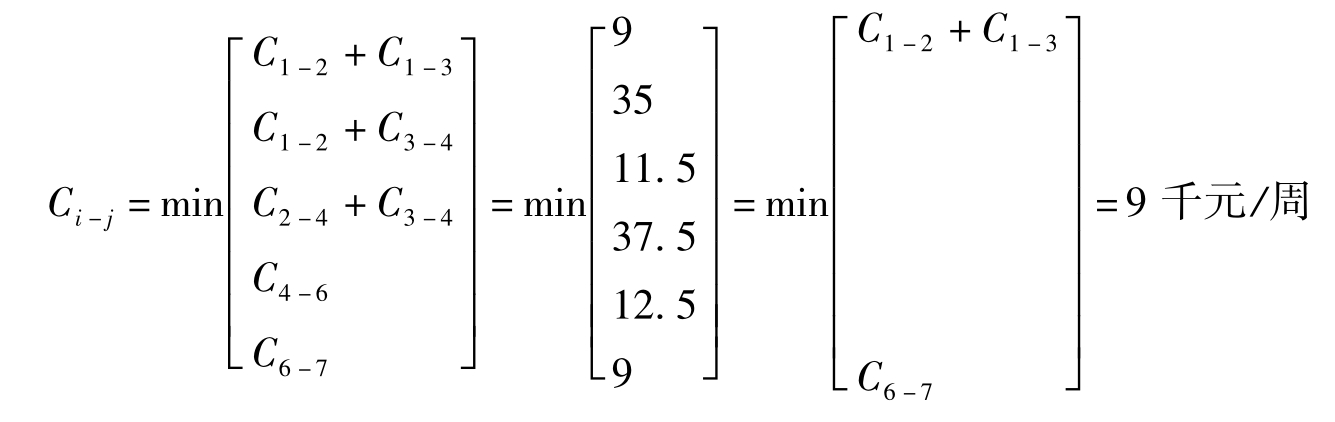
则可同时压缩工作①－②和①－③组合，或压缩工作⑥－⑦的持续时间

(3)确定工作⑥－⑦的压缩时间

假设工作⑥－⑦压缩时间为4－1=3周，工作④－⑤和⑤－⑦的总时差为5周，允许在这部分关键线路上关键工作的压缩时间最多为5周，则工作⑥－⑦的压缩时间Δt₂=3周，使d_6－7=1周。

(4)压缩后工期T₂=T₁－3=24－3=21周

增加的直接费用ΔC₂=9×3=27千元

第二次压缩后网络计划的时间参数变化只有工作F、H、I，其参数见表6-9。

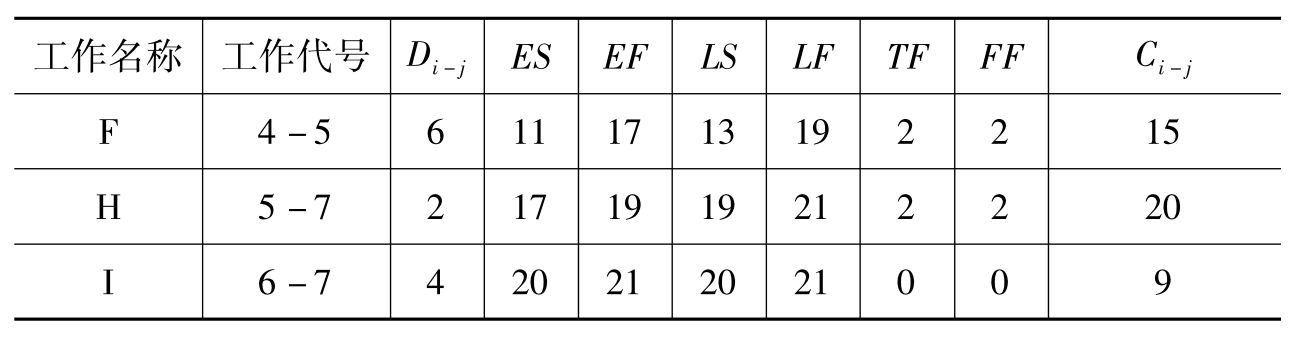
表6-9　第二次压缩后网络计划的时间参数

第三次压缩关键工作的持续时间：

(1)确定关键线路，即①－②－④－⑥－⑦和①－③－④－⑥－⑦，找出关键线路的关键工作为A、C、G、I和B、D、G、I。

(2)从第二次压缩中，我们可以知道关键工作①－②和①－③的组合直接费用率最小即C_i－j=9千元/周。

(3)确定工作①－②和①－③组合的压缩时间

关键工作①－②和①－③要共同压缩相同的时间，才会使整个工期时间缩短，则应缩短工期Δt₃=min(Δd_1－2，Δd_1－3)=min(4，1)=1周，使得

D_1－2+D_2－4=D_1－3+D_3－4=10周

(4)压缩后，工期T₃=21－1=20周

增加直接费ΔC₃=9×1=9千元

该网络计划经过三次压缩后，其网络计划如图6-30所示。

图6-30

确定关键线路为①－②－④－⑥－⑦和①－③－④－⑥－⑦两条，工期T=20周，满足合同要求，增加直接费用C=8+27+9= 44千元。