空间经济学与国际贸易

第一节　空间经济学

空间经济学是在区位论的基础上发展起来的多门学科的总称。它研究的是空间的经济现象和规律，研究生产要素的空间布局和经济活动的空间区位。在克鲁格曼等经济学家的努力下，经济活动的空间区位对经济发展和国际关系的重要作用异乎寻常地引起了人们的高度重视，空间经济学也因此成为当代经济学中最激动人心的领域之一，空间经济理论被视为不完全竞争与收益递增革命的第四次浪潮。

一、空间经济学的渊源和发展

(一)空间经济学的历史渊源

德国学者冯·杜能在1826年撰写了巨著《孤立国同农业和国民经济的关系》，以一种全新的方式诠释并分析了地租和土地利用，而他对孤立国(城市)的描述，成为空间经济学发展的起源。

韦伯在1909年撰写了《工业区位论》，建立了一系列概念、原理和规则，严谨地表述了一般的区位理论，并发展成为空间经济学的另一个流派。

新古典区位理论代表人物沃尔特·克里斯塔勒(Walter Christaller)于1922年出版了《德国南部的中心地区》，提出了中心地区理论(Central Place Theory);而另一代表人物奥古斯特·勒施(August Losch)在1939年出版了《区位经济学》，以最概括性的语言将一般均衡理论应用于空间研究。

1956年，沃尔特·艾萨德(W.Isard)出版了《区位和空间经济》一书，将上述几位学者的模型整合为一个统一、易于分析的框架，把区位问题简化为一个简单的比较选择问题，即厂商要权衡运输成本和生产成本，从而做出区位选择。他的这种做法具有开创性。但是，正如克鲁格曼(2000)所说:艾萨德想要将空间问题带入经济理论的核心，却从未实现，事实上，他并未提出过一个一般区位均衡的例子……不过，他开创了一个折中的应用领域——区域科学。

阿隆索(Alonso.W)在1964年出版了《区位和土地利用》一书，用经常在城市和农村之间穿梭的通勤者(Commuters)替代农民，用中央商业区(Central Business District，CBD)替代城市，建立了一个单中心城市模型，描绘了一幅比冯·杜能的模型更让人憧憬的蓝图。

将区位理论与国际贸易密切联系起来的是贝蒂尓·俄林(B.G.Ohlin)，他获得1977年诺贝尔经济学奖时，其名著《区际贸易与国际贸易》被提名为他的主要贡献。俄林架起了贸易与区位理论之间关系的桥梁。

(二)空间经济学的发展

1952年，美国著名经济学家保罗·萨缪尔森(Paul Samuelson)发表了《转移问题和运输成本:障碍缺失时的贸易条件》(The Transfer Problemand Transport Costs:The Terms of Trade When Impediments are Absent)一文，创造了“冰山成本”的概念。本来在传统的贸易理论中是不考虑运输成本的，但现实贸易中运输成本是客观存在的，萨缪尔森并不特别描述运用资金和劳动力提供运输服务的行业，相反，他建议人们想像货物在运输途中被“融化”了一些，最终只有一部分能到达目的地，损失的那一部分便是运输成本。“冰山成本”形式的运输成本很巧妙，它极大地简化了模型的交易成本部分，并且便于分析和计算。这种极其聪明的运输成本形式，在空间经济学领域以及经济学的其他领域都得到了广泛应用。

1977年，迪克西特(Avinash Dixit)和斯蒂格利茨(Joseph Stiglitz)在《美国经济评论》上发表了著名的文章《垄断竞争和最优产品多样性》(Monopolistic Competition and Optimum Product Diversity)，以英国剑桥大学的罗宾逊(J.Robison)和美国哈佛大学的张伯伦(Edward Chamberlin)于1933年提出的垄断竞争思想为基础，构建了一个非常精巧而独特的Dixit-Stiglitz垄断竞争模型。该模型为经济学很多领域的研究提供了崭新而方便的工具，扫除了技术障碍，从此，掀起了经济学研究中收益递增和不完全竞争的革命。这场革命有四波:第一波是产业组织理论，第二波是新贸易理论，第三波是新增长理论，第四波是空间经济理论。

克鲁格曼是这场革命的弄潮儿。以迪克西特-斯蒂格利茨的垄断竞争模型为基础，借鉴国际贸易理论，利用保罗·萨缪尔森(1954)的“冰山交易成本”技术，克鲁格曼在1991年发表了《收益递增和经济地理》一文，把空间概念引入迪克西特-斯蒂格利茨的垄断竞争一般均衡分析框架中，完成了新经济地理学的开山之作，即中心—外围模型(Core-Periphery Model，简称为CP模型)。

正如藤田昌久、克鲁格曼和维纳布尔斯(1999)在《空间经济学》中所指出的那样，空间经济学是以“迪克西特-斯蒂格利茨的垄断竞争模型、‘冰山成本’技术、动态演化和计算机”为标志的。迪克西特—斯蒂格利茨的垄断竞争模型和‘冰山成本’技术是空间经济学的理论基础，“动态演化”是指CP模型中存在多重均衡，现实经济会选择哪种均衡是不确定的，此时，历史、偶然事件和人们的预期会起到非常重要的作用。在CP模型中，长期的稳定均衡是由一组非线性方程组给出的，不过这组方程组的解很难用解析解形式表达出来，因此，CP模型的很多结论必须依赖计算机的数值模拟来得出。

当然，在空间经济学这片新的乐土上，从克鲁格曼开创新经济地理学(New Economic Geography)以来，已经有大量文献涌现出来，其中不乏经典之作，如鲍德温(Baldwin)等在2003年出版的《经济地理和公共政策》(Economic Geography and Public Policy)一书，则大大推进了空间经济学的政策应用。

(三)空间经济学的发展方向

空间经济学至少有三个可供未来研究的重要方向:扩展理论菜单、寻求实证研究以及探讨空间经济的福利与政策含义。

集聚力(或者向心力)和分散力(或者离心力)是空间经济学研究的主要内容。集聚力来自关联效应、厚实的市场、知识溢出和其他外部经济，而分散力来自于不可流动的生产要素、土地租金或者运输成本、拥塞和其他外部不经济。当然，还可以考虑集聚力和分散力的其他来源，以扩大这一理论菜单。

另外，理论是从现实中抽象出来，并且反过来要用来为现实服务的。因此，在未来的研究中，可以用事实和数据来验证空间经济学的理论，也可以探索空间经济学的福利含义，以及它对现实经济活动、政策上的指导意义。事实上，克鲁格曼的工作业已产生了重大的政策影响，世界银行2009年世界发展报告《重塑世界经济地理》就是空间经济学政策应用和分析的最好例证。当然，为了让克鲁格曼的工作体现出更大的价值，很多工作仍然等待着我们。

二、克鲁格曼的中心—外围模型^[1]

克鲁格曼中心—外围模型的主要目的，是要用尽可能简单明了的语言和模型，来清晰地说明厂商层面的收益递增、运输成本和要素流动三者之间的相互作用是如何引起空间经济结构的形成和变化的。

(一)基本假设

1.假设经济系统中只有农业部门A和制造业部门M。农业部门是完全竞争的，生产单一的同质产品。当然，我们没必要拘泥于“农业”的字面含义，可以把农业部门看作是从事制造业之外生产活动的完全竞争部门。制造业部门则是不完全竞争的，而且具有收益递增的特征，供给大量的差异化产品。假定存在大量潜在的制造品，因此可以把整个生产空间看成是连续的，这样就能够避开产品数量必须是整数的限制。

2.假设每个企业只生产其具有规模报酬递增的一种产品，不会选择范围经济，这意味着每个企业与其所生产的产品是一对一的关系，即每个企业只生产一种产品，这使得厂商在其所生产的产品上具有一定的垄断性。尽管厂商是垄断竞争的，但其所在生产部门不是自然垄断行业部门，也不是从政府获得特许权从事生产的部门，这意味着市场上存在许多潜在进入企业，并且潜在企业可以随时、无障碍地进入或退出每个行业。所以垄断厂商定价不能按照垄断价格定价，其最优的定价策略是边际成本加成定价，均衡时其超额利润为零。也就是说，尽管制造业厂商具有垄断厂商的特征，因为在其所在行业其市场占有率是100%，但其市场行为与完全竞争市场上的厂商行为是一样的。同时，假定企业的自由进出是瞬间完成的，所以超额利润总是零。

3.假设消费者偏好差异化产品，不同产品之间具有一定的不变替代性σ。

4.假设两个部门分别仅使用一种劳动力资源进行生产，即农民和工人，并且各部门的要素供给量不变。在不同区域之间，农民不可流动，而工人可以自由流动。

5.假设世界上只有2个地区，这2个地区在偏好、技术、开放度以及初始的要素禀赋方面都是对称的。农民总的数量为L^A，并且农业在两个地区平均分布。与此相对应，制造业的劳动力是随时间变化的，世界工人总数为L^M，λ为地区1在任何时点上的制造业劳动力份额，(1－λ)为地区2在任何时点上的制造业劳动力份额，并且可以适当地选择单位使得L^M=μ，L^A=1－μ。

6.采用“冰山成本”形式来表示制造业产品的运输成本，即如果要使得1单位产品到达目的地，在启运地就需要装运T单位产品，而农产品的运输是不需要成本的。

7.由于农产品的运输是免费的，并且规模报酬不变，所以各地区农民的工资率相同，农产品的价格也相同，可标准化为w^A=1，p^A=1。而各地区的制造业工人工资可能会有所不同，各地区制造品i的价格p(i)可能也不相同，w₁和ω₁分别是地区1的制造业工人的名义工资和实际工资。

(二)基本模型

1.消费者方面

对两类产品来说，所有的消费者都具有相同的偏好，代表性消费者的效用函数由柯布-道格拉斯(Cobb-Douglas)函数形式表示:

U=M^μA^1－μ，　　　　　　　　　(5.1)

其中，A是农产品的消费量;μ是常数，表示对制造品的支出在总支出中所占的比重;M代表制造品消费量的综合指数，是分布在连续区间上的各类制造品的子效用函数，假定M符合不变替代弹性(CES)函数:

该式中，m(i)表示对每种可获得的制造品i的消费量;n是制造品的种类范围，通常称为可获得的制造品种类的数目。参数ρ表示消费者对每种制造品的偏好程度。当ρ趋近于1时，差异化产品几乎是完全替代的;ρ趋近于0时，消费更多种类差异化产品的愿望越来越强。令σ≡1/(1－ρ)，则σ表示任意两种制造品之间的替代弹性。

对任意一种制造品的需求m(i)，需要在约束条件下求解支出最小化的问题:

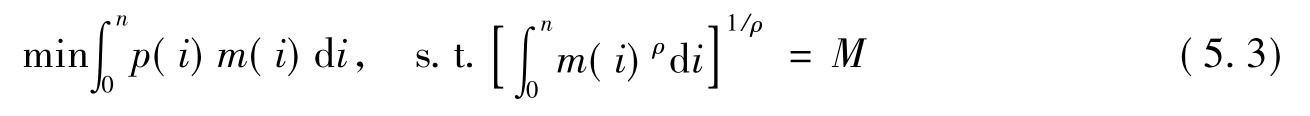
经过求解可得:

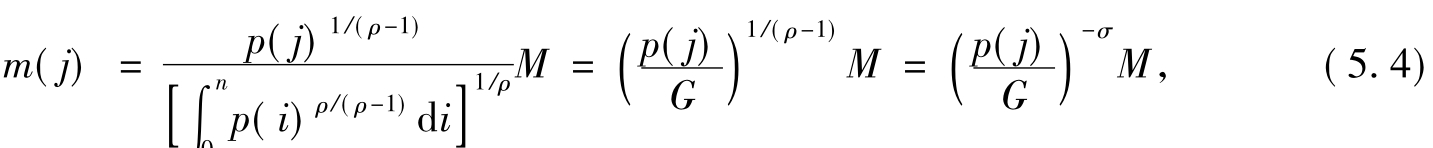
其中，制造品的价格指数

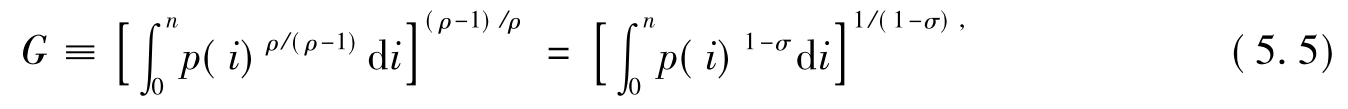
给定收入Y，农产品的价格p^A被标准化为1，p(i)是制造品种类i的价格，那么消费者的问题就是在下面的预算约束条件下使其效用最大化，maxU=M^μA^1－μ，s.t.A+GM=Y，经过求解可以得出以下表达式:

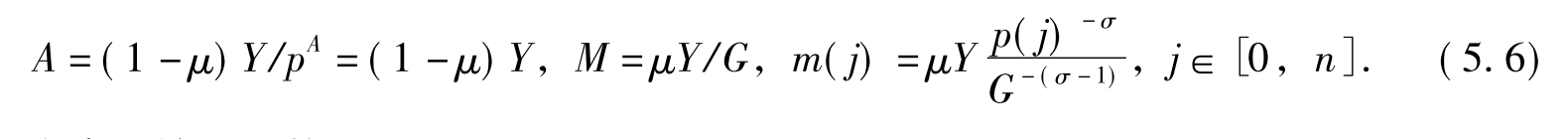
把(5.5)式代入效用函数得:

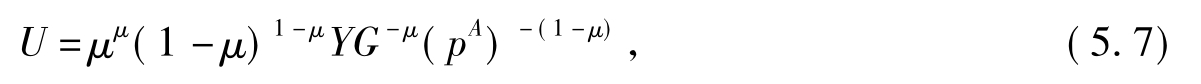
其中，G^－μ(p^A)^－(1－μ)是该经济体的生活费用指数(Cost-of-living Index)。

显然，Dixit-Stiglitz模型的与众不同之处(而且在我们的分析中起关键作用)是出售的制造品种类n是一个内生变量，并且是连续的。所以，我们有必要了解制造品种类n的变化对消费者的影响。

假定所有可得到的制造品价格都是p^M。价格指数(5.5)式可以简化为:

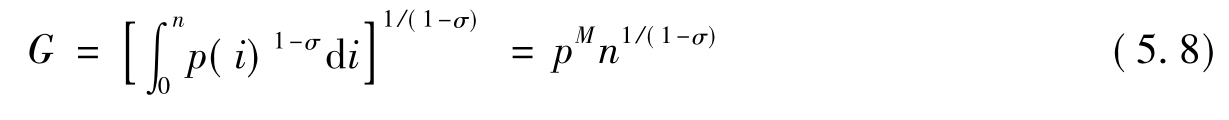
价格指数对可得制造品数目的敏感度取决于不同种类制造品之间的替代弹性σ，σ越低(即各种产品间的差异性越大)产品种类增加引起价格指数下降的幅度就越大。随着出售的制造品种类的增加，制造品价格指数随之下降，获得给定效用水平的成本也随之降低。

2.生产者方面

假设所有区位所有制造品的生产技术都相同，固定投入为F单位的劳动，边际投入为c^M单位的劳动。生产中只有一种要素投入是劳动，在给定区位生产数量为q^M的任何产品需要的劳动投入为l^M，即:

l^M=F+c^Mq^M　　　　　　　(5.9)

对于位于r地区的厂商生产一种特定产品，该企业工人的工资率是给定的w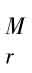，产品的出厂价为p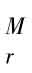，则利润可表示为:

在价格指数G_S给定为常数的情况下，假定所有厂商都选定各自的产品价格，根据利润最大化原则可知对于所有区位r生产的产品种类有:

若定价原则是给定的，那么位于地区r的厂商的利润为:

所以，零利润条件意味着任何灵敏厂商的均衡产出为:

相应的均衡劳动力投入为:

l^*≡F+c^Mq^*=Fσ

因此，如果L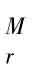表示地区r的制造业工人数量，n_r表示地区r的制造业厂商数目(恒等于制造业的产品种类数)，那么: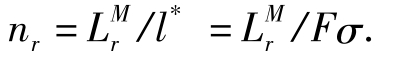

从(5.11)式和(5.13)式可知，市场规模既不影响边际成本加成定价(Markup of Price over Marginal Cost)也不影响单一产品的生产规模，因此所有的规模效应都是通过产品种类的变化发生作用的。

3.工资、收入等

把地区1和地区2综合起来考虑，结合前面的式子可得出下列方程:

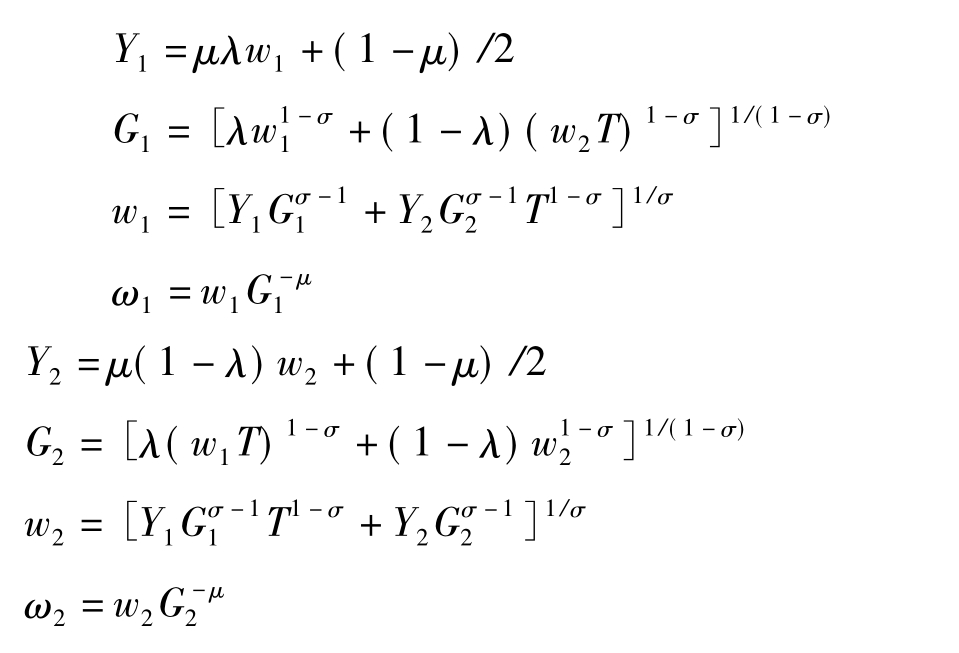
这8个非线性方程无法得到解析解，需要运用数值模拟。

4.数值模拟

图5.1、5.2和5.3都是经过数值模拟而得出的结果，其中(ω₁－ω₂)是两个地区制造业的实际工资率差额，λ是地区1的制造业份额，σ=5，μ=0.4，不过运输成本T各不相同，三个图的运输成本依次下降。

在图5.1中，当λ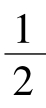＜时，工资差额为正，反之为负。说明若一地区拥有超过半数的制造业劳动力，那么该地区对工人的吸引力就不如另一地区。此时，经济将收敛于长期对称均衡，制造业在两个地区平均分布。

在图5.2中，运输成本处于中等水平，此时，存在5个均衡:3个稳定均衡(即图中的实心点，对称均衡和制造业集中在任一地区的均衡)和2个不稳定均衡。

在图5.3中，运输成本最低，工资差额随λ单调上升。这表明若其中一地区制造业份额越大，该地区就越有吸引力。最终的均衡是制造业完全集中在其中任一地区的中心—外围模式。

结合上述例子来看图5.4，实线表示稳定均衡，虚线表示不稳定均衡。若运输成本足够高，则存在唯一的对称稳定均衡，制造业在两地平均分布;若运输成本降到某一临界水平之下，制造业就集中在一个地区，产生新的均衡;若运输成本继续下降至另一临界水平之下，对称均衡就成为不稳定均衡。图中T(B)为突破点，在该临界点上，两地的对称均衡是不稳定的，会被打破;T(S)为支撑点，在该临界点上，中心—外围模式一旦确立就能维持下去。

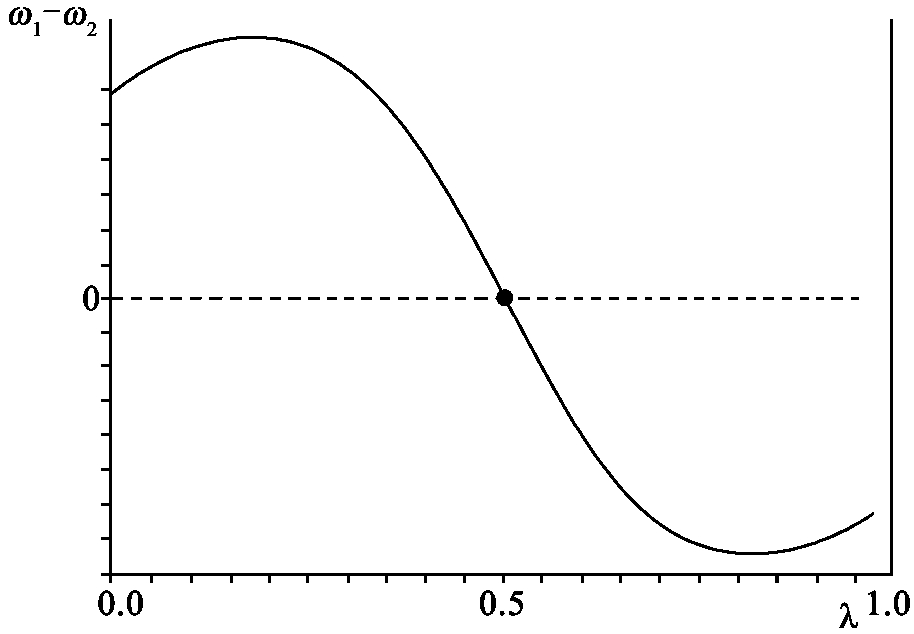
图5.1　T=2.1

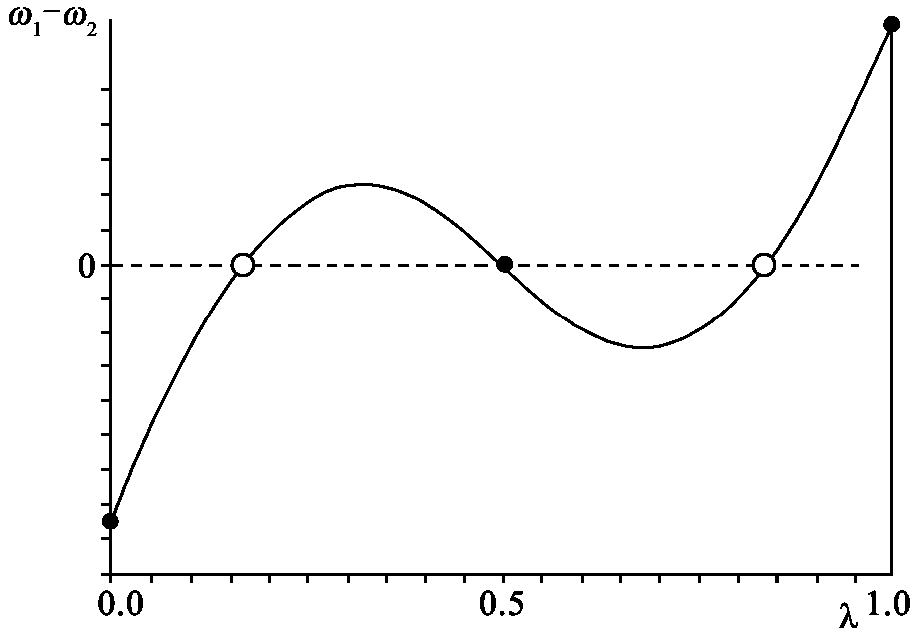
图5.2　T=1.7

5.“非黑洞”条件

倘若一个经济体的规模报酬递增特别明显，说明集聚力在该经济体中占据了绝对优势，经济体最终会塌陷为一个点，也就是说，该经济体最终会毫无疑问地形成绝对的中心—外围结构。对于这样的经济体，也就没有研究的必要了，因为不管怎样，其结果是唯一确定的。

为了避开这种“黑洞区位”(Black-hole Location)理论，通常要加上一个非黑洞假设(Assumption of no Black Holes)，即: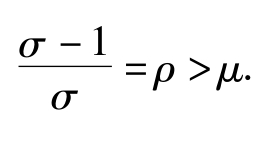

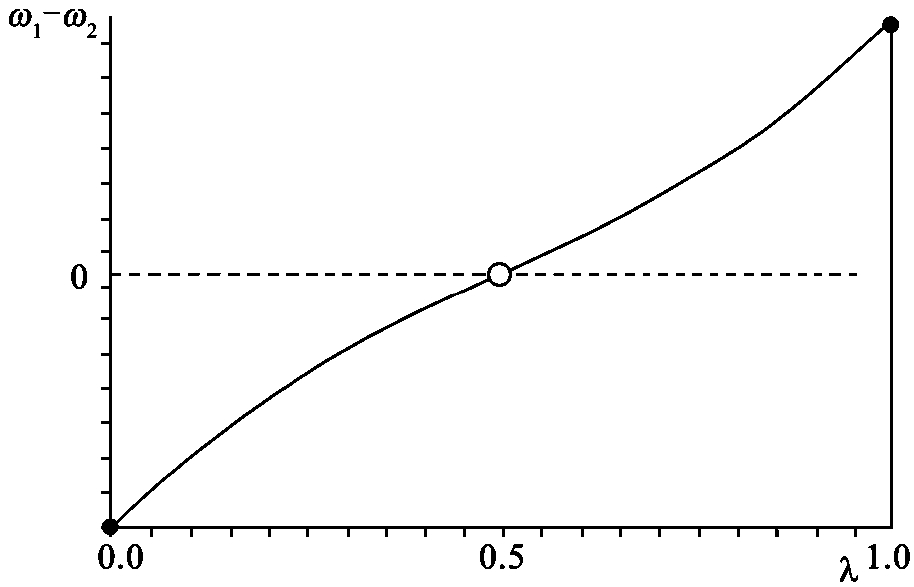
图5.3　T=1.5

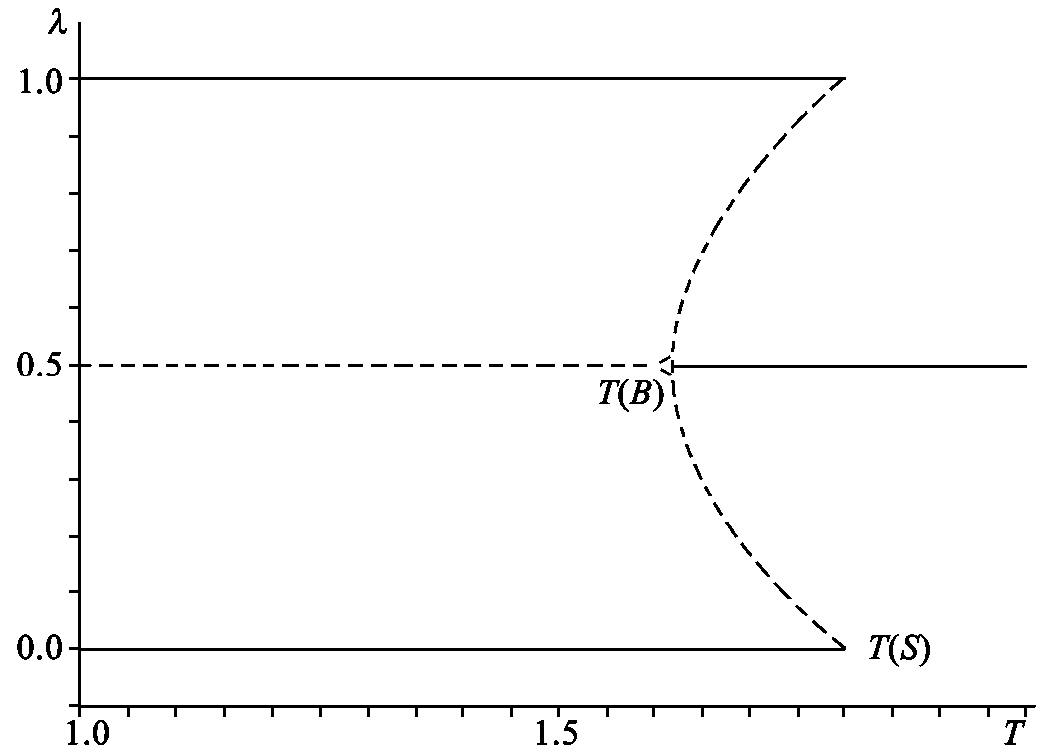
图5.4　中心-外围分岔

三、空间经济学的核心结论

在克鲁格曼的CP模型之后，理论进展一方面是提高CP模型的可解性，另一方面是扩展集聚力和分散力的初始菜单。但从根本上来说，后来的模型所展现的主要信息与克鲁格曼的CP模型是一样的:经济活动的空间分布以及经济个体的潜在区位决策，都是集聚力与分散力之间非线性互动的内生结果。更为重要的是，即便建立了用来分析很多不同问题的模型，结果发现这些模型都有相似的“深层结构”(Deep Structure):虽然参数表达形式稍有不同，但相同的问题不断出现，模型中经济的定性行为通常产生几个相同的表达式，这些表达式反映了集聚力和分散力之间的相互作用。这些模型都展现了相同的空间经济学核心结论。

(一)本地市场效应

本地市场效应是中心—外围模型的关键性特征之一，也是集聚力之一。它是指若某种外生冲击改变原有需求的空间分布，扩大其需求，则大量企业将会改变其原有区位，向该区域集中。简单地说，本地市场效应就是需求增加一定比例会带来产出更大比例的增加。

(二)循环因果关系

经济活动空间分布是由集聚力和分散力共同作用、相互权衡的结果。集聚力一般包括两种力量:一种是本地市场效应或者市场接近效应，又称为后向联系;另一种是价格指数效应或者生活成本效应(是指生产活动向某一区域的集中导致该区域相对价格指数的下降，而名义收入不变，则实际收入水平提高)，又称为前向联系。分散力主要指企业之间相互竞争而导致的一种离心力，称为市场竞争效应或者市场拥挤效应。循环累积因果关系是指本地市场效应和价格指数效应相互成为因果关系。假设存在某种外生的冲击，使得劳动力或企业向某一区域集聚，扩大了该区域的市场规模和供给能力，以利润最大化为目标的企业会选择市场规模较大的区域。反过来，某一区域集中了很多企业，则本地生产的产品种类和数量增多，进口减少，价格指数下降，在名义工资不变时，实际工资上升，从而会吸引更多的工人和企业选择该区位。本地市场效应和价格指数效应成为因果关系，也就是前后向联系，进一步放大了初始冲击对经济系统的影响。

(三)内生的非对称性

内生的非对称性是指，初始时对称的两个区域，随着交易成本的逐渐下降，最终变成非对称的两个区域。空间经济学研究的对象主要是初始时对称的均质空间，主要探讨经济系统的内生力量是如何决定空间分布模式的。把空间因素引入经济模型，就必须考虑因空间而产生的成本问题，即交易成本，既包括运输成本，也包括各种制度成本。空间经济学研究的一个重要结论是集聚力和分散力通常都随着交易成本的下降而下降，但分散力的下降相对更快一些。在交易成本较大时，分散力也会较大，此时市场拥挤效应占优势，使得对称均衡分布得以稳定存在。随着交易成本的下降，超过某一临界值(即突破点)，集聚力开始大于分散力，对称均衡被打破，经济活动会向某一区域集中。

(四)突发性集聚

当对称均衡稳定且贸易自由度很小(即交易成本很大)时，贸易自由度的提高不会影响经济活动的区位问题;但当贸易自由度达到某一临界值(即突破点)后，自由度稍微增加，就会发生突发性集聚，使得所有经济活动集中在某一区域。

(五)区位的黏性

中心—外围模型的另一个突出特征是区位黏性，也即“路径依赖”，不过这种情况在贸易自由度大于持续点的贸易自由度，也就是中心—外围模型具有多重均衡时，才会发生。此时，历史事件、人们的预期或某种区域政策起主要作用。经济不断向中心—外围结构逼近，但不会变为中心—外围结构的稳定均衡状态，倘若这时来一个短暂冲击，比如某一区域对生产活动实行暂时补贴政策，则促使经济系统从对称均衡转入中心—外围模式的稳定均衡状态。但这种暂时冲击消失后，经济系统不会自动恢复到冲击之前的稳定状态，这就是区位的黏性。

(六)“驼峰状”集聚租金

集聚租金是指当完全集聚是稳定均衡时，工人从中心区转移到外围区时所遭受的损失。集聚租金是贸易自由度(φ=T^1－σ表示贸易自由度，φ∈［0，1］，T=1时，φ=1;T→∞时，φ=0)的凹函数，当φ=φ^S和φ=1时，集聚租金为零;当φ^S＜φ＜1时，租金为正;当φ=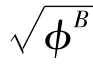时，租金取最大值(其中φ^B是对应于图5.4中T(B)点的突破点，φ^S是对应于T(S)点的持续点)。随着自由度φ从φ^S提高到1，租金曲线先升后降，呈“驼峰状”。

(七)叠加区和预期的自我实现

在中心—外围模型中，当自由度在区间(φ^B，φ^S)内变动时，对称结构和两种中心—外围结构都是局部的稳定均衡，区间(φ^B，φ^S)称为叠加区。这说明当劳动者的预期突然发生变化时，劳动者将根据变化后的预期任意选择对称结构或中心—外围结构作为其工作和居住区位。这种任意选择区位时的主要依据是个体认为大多数人选择的某种经济模式可能是最有效的，从而该个体也会选择大多数人所选择的经济模式。这样，人们预期的变化将把经济系统推向另一种经济模式。不过，这些都是在满足“非黑洞”条件情况下才成立的。