单因素敏感性分析计算公式

第三节　敏感性分析

敏感性分析则是分析各种不确定性因素变化一定幅度（或者变化到何种幅度）时，对方案经济效果的影响程度（或者改变对方案的选择），而把不确定性因素当中对方案经济效果影响程度较大的因素，称之为敏感性因素。不确定性因素变动的范围越小，而造成的经济效果变动范围越大，则敏感性越强。敏感性分析的主要任务是确定方案的敏感性因素，计算各因素的敏感程度，分析方案所能承受的风险，为提高方案预测的可靠性和决策的准确性提供依据。

敏感性分析按敏感因素每次变动数目的不同，可分为单因素敏感性分析和多因素敏感性分析。

一、敏感性分析的步骤及主要内容

敏感性分析的步骤见图5－5，其主要内容包括：

图5－5　敏感性分析步骤

（一）确定分析对象（指标）

由于投资效果可用多种指标来表示，在进行敏感性分析时，首先必须确定分析指标。当投资者所关心的目标不同时，所侧重的经济指标也不尽相同：如果主要分析方案状态和参数变化影响方案投资回收的快慢，则可选用投资回收期作为分析指标；如果主要分析产品价格波动影响方案的超额净收益，则可选用净现值作为分析指标；如果主要分析投资大小影响方案的资金回收能力，则可选用内部收益率等。当方案评价所处的阶段和深度要求不同，选用的经济评价指标亦有区别：如果在方案机会研究阶段，深度要求不高，可选用静态的评价指标；如果在详细可行性研究阶段，则选用动态指标评价。

（二）选择敏感因素

从理论上讲任何一个因素的变化都会对投资效果产生影响，但在实际分析中并没有必要对所有可能变化的因素都进行敏感性分析。选择敏感性分析的主要不确定性因素，主要考虑：（1）这些因素在可能的变化范围内，对投资效果影响较大；（2）这些因素发生变化的可能性较大，通常包括：项目总投资、项目寿命期、产品价格、销售量、经营成本、基准贴现率等。

（三）确定变化范围

敏感因素的变化范围可用相对数或绝对数表示，通常使用相对数。相对数是指每个敏感因素都在原来取值的基础上向上或向下浮动一定的百分比，如±10%、±20%等。具体的取值范围可根据项目实际情况确定。

（四）计算影响程度

根据敏感因素的变化范围，当计算某特定因素变化所产生的影响时，假设其他因素保持不变。将该因素按一定幅度变化，计算相应的评价指标的变动结果，将计算结果列表或作图，以便于测定敏感因素。

（五）确定敏感因素和临界值

测定某特定因素敏感与否，可采用两种方式进行。第一种方式：假定需分析的因素均从基准值开始变动，且各因素每次变动幅度相同，通过计算并比较每次变动对经济指标的影响效果，就可以判别出各因素的敏感程度。第二种方式：假定某特定因素向降低投资效果的方向变动，并设该因素达到可能的“最坏”值，然后计算在此条件下的经济指标，看是否已达到使项目在经济上不可取的程度，如果项目已不能接受，那么该因素就是敏感性因素。

（六）因素敏感性排序

根据敏感性分析的结果，对因素敏感性进行初步排序，也可根据项目的实际情况进行适当的调整。

二、单参数敏感性分析

每次只变动一个不确定性因素，而其他参数保持不变时所进行的敏感性分析，叫做单参数敏感性分析。

【例题5－4】某投资方案预计总投资为1 000万元，年产量为10万台，产品价格为30元/台，经营成本为100万元，方案经济寿命期为12年，届时设备残值为85万元，基准贴现率为10%。试对总投资额、产品价格及贴现率进行敏感分析。

解：本题以净现值作为经济评价指标，设总投资额、产品价格、贴现率三个不确定性因素分别为T、P、i。

NPV＝－T＋（P×10－100）（P/A，i，12）＋85（P/F，i，12）

其中，基准方案的净现值为：

对T、P、i逐一按在基准值基础上变化±10%、±20%、±30%取值，所对应的方案净现值结果见表5－3和图5－6。

表5－3　单参数的敏感性计算　　单位：万元

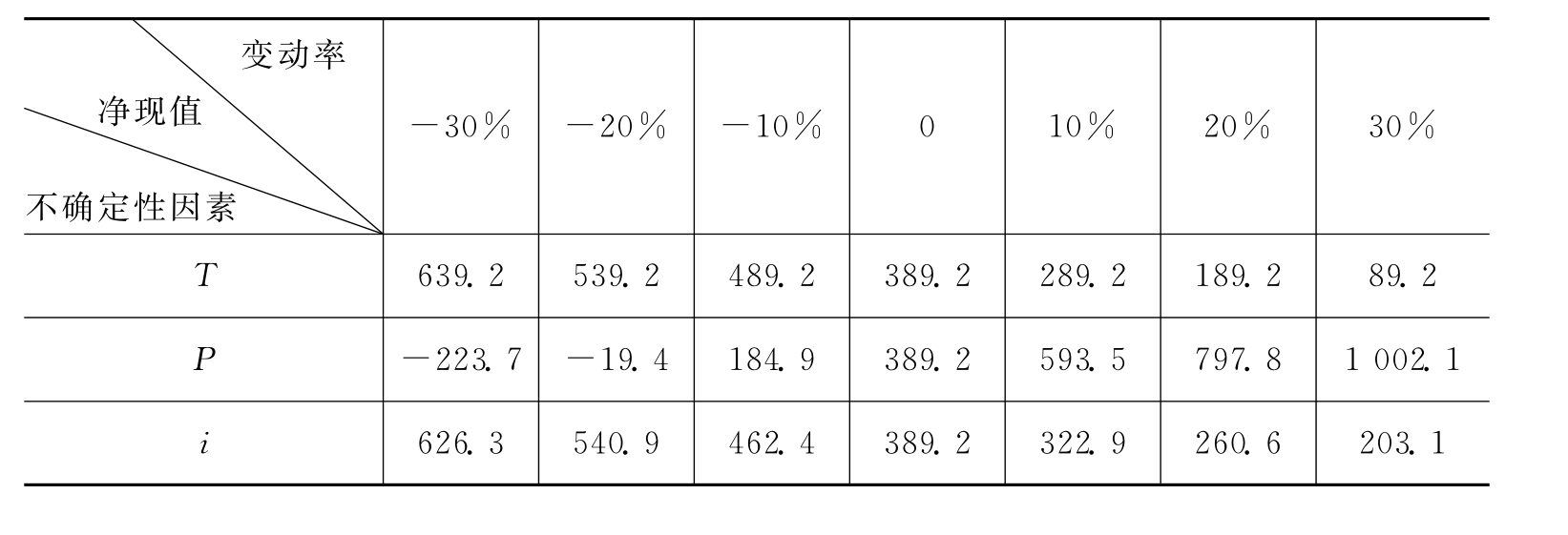
图5－6　敏感性分析图

从表5－3和图5－6可以看出，在同样的变动率下，产品价格的变动对方案的净现值影响最大，其次是投资额的变动，贴现率变动的影响最小。计算结果表明，当实际投资额超出预计投资额的38．9%，或者当产品价格下降率比预计价格低19．5%，或者贴现率上升率比预计贴现率高52．5%时，NPV＜0，方案变得不可接受。

对于本方案来说，产品价格是敏感因素。如果未来产品价格变动的可能性较大，则意味着这一投资方案的风险亦较大。

三、多参数敏感性分析

单参数敏感性分析是假设某一参数变动而其他参数不变时对投资项目经济效益的影响，但实际上各不确定性因素变化对项目经济效益的影响是交叉地、综合地发生的，若要考虑这种情况，则必须进行多参数的敏感性分析。

（一）双参数敏感性分析

每次同时变动两个不确定性因素，并且变动幅度是相同的敏感性分析，叫做双参数敏感性分析。

【例题5－5】沿用例5－4数据，假定总投资额和价格是关键因素，对这两个因素进行双参数敏感性分析。

解：设x表示总投资额T变化的百分比，y表示产品价格P变化的百分比，则：

NPV＝－1 000（1＋x）＋［30（1＋y）×10－100］（P/A，10%，12）＋85（P/F，10%，12）＝389．2－1 000x＋2 043y

当NPV≥0时，方案可行，故有y≥0．49x－0．19，将该不等式绘成一空间平面，就可得到双参数敏感性分析图。其中，y＝0．49x－0．19为投资方案盈亏平衡线，它把X－Y平面分为两个区域，盈利区和亏损区。从图5－7中可以看出，该投资方案对产品价格最敏感。

图5－7　双参数敏感性分析图

（二）三参数敏感性分析

每次同时变动三个不确定性因素的敏感性分析，叫做三参数敏感性分析。

【例题5－6】仍沿用例5－4数据，假定总投资额、产品价格和年经营成本为关键因素，对这三个因素进行三参数敏感性分析。

解：设x表示总投资额变化的百分比，y表示产品价格P变化的百分比，z表示年经营成本变化的百分比，则：

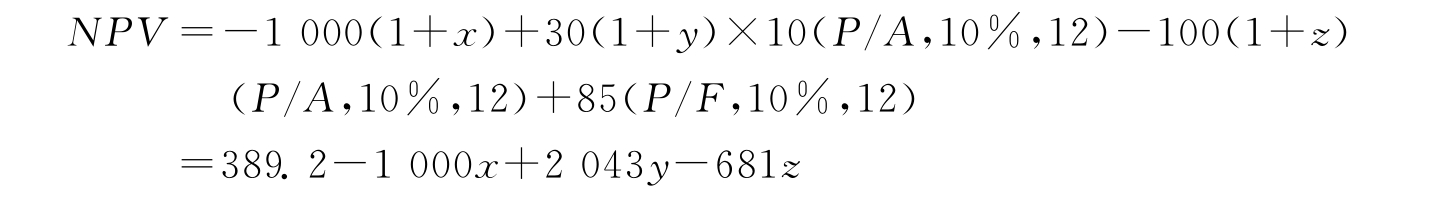
当NPV≥0时，方案可行，即－1 000x＋2 043y－681z＋389．2≥0，将该不等式绘成一空间平面，就可得三参数敏感性分析图，此空间平面将三维空间分成两部分：包括原点的空间NPV＞0（见图5－8）。从图中可以看出，该投资方案对产品价格最敏感，其次是总投资额，再次为年经营成本。

对于多于三个参数的敏感性分析，作图显然不方便，可用偏导数方法解析求之。

图5－8　三参数敏感性分析图

（三）敏感性分析的思考

敏感性分析在一定程度上描述了不确定性因素的变化对投资效果的影响，有助于决策者了解影响投资效果的关键因素。但是在敏感性分析中“各因素在未来的变动概率相等”这一假设并不完全符合实际。因此，对不确定性因素进行分析时，还必须考虑因素变化的可能性大小，对它们进行概率分析。