互惠合作模型及稳定性分析

一、互惠合作模型及稳定性分析

（一）互惠合作模型

一般地，我们假设一群农民面临着“囚徒困境”式的合作问题，其理论程式如表1所表示。为了便于讨论，但又不失一般性，这里给出有具体数字的结构：

表6—1　囚徒困境：具体例子

在一个随机成对匹配的无穷重复囚徒困境（IRPD）中，我们假设参与农民总属于下面三种类型中的一种：（1）无条件合作的人，其比重为x₁，并在每一阶段都选择行动C；（2）机会主义的人，其比重为x₂，并在每一阶段都选择行动D；（3）互惠⁽¹⁾主义（Reciprocity）的人，其比重为x₃，策略是开始选择C，以后每个阶段都模仿对手上一阶段的行动，这个策略（记为R）充分体现互惠行为的三个特征：①善良：主动选择合作，并期望对方也会选择合作；②不可欺：对于对方的背叛，将在下一次博弈中选择不合作以示惩罚；③宽容：容易原谅对手曾经选择过不合作，只要对方“改过”，即以合作对待。

虽然我们假设每个博弈阶段每个农民都属于某种类型，但由于模仿等原因，每个人的所属类型会发生变化，比如成功的行为很快就会被学习和模仿，这种机制就是著名的复制者动态（RD）⁽²⁾，即每个时期某种类型的人所占百分比的变化与该类型人当前的福利水平和全体人口的平均福利水平的差异成正比。因此，若某类型人当前的福利水平高于平均水平，他们在人口中的比例将会上升；如果某类型人当前的福利水平低于平均水平，他们在人口中的比例将会下降；当该类型人的福利水平正好处于平均水平，则他们的比例将维持稳定。

由于是重复博弈，我们需要设定参与人对未来的重视程度，这里假定农民的跨期支付按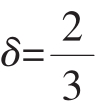进行贴现⁽³⁾，那么容易验证IRPD的策略形式为下面的支付矩阵：

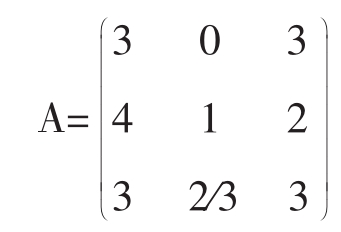
其中策略的顺序标记为j=1，2，3。

考察这一情况下的复制者动态，因为群体状态x=（x₁，x₂，x₃）属于两维单形，因而只要描述其中两个频率就足以刻画RD的运动法则。具体地，我们选择x₂（不合作策略D）和x₃（互惠策略R），群体的平均收益为：

现在我们得到含有互惠主义群体的均衡状态，包括：

①（x₂，x₃）=（0，1），即系统稳定时所有人都成了互惠主义者。

②集合：H={（0，x₃）∶0≤x₃≤1}，即机会主义行为消失也有可能是RD的均衡点。

在以上三种均衡状态下，互惠主义者都能获得生存空间，特别是在第一种均衡中，互惠主义者最为成功，因为他们的行为最终被所有的无条件合作者和机会主义者所学习和模仿。但是什么条件下，所有机会主义者会被互惠主义所同化呢？为此，我们考虑：

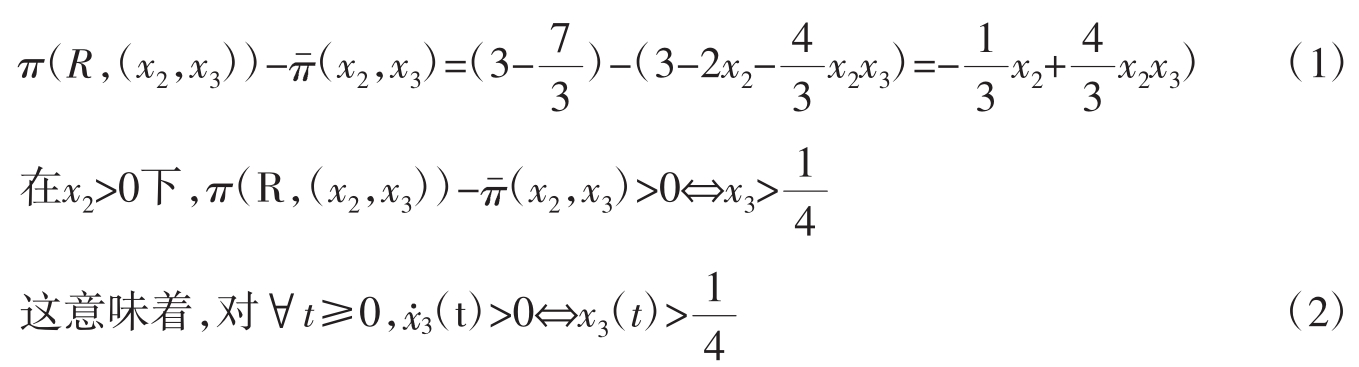
这个简单的结果意味着：群体在长期状态下是合作的情况，当且仅当互惠主义的初始数量足够高时才会发生，这样我们彻底展示了互惠这支“看不见的手”在指引群体合作中的关键作用。

（二）互惠合作模型的稳定性分析

一般而言，农村社区是一个熟人社会的交往结构，在这样的结构下，社区成员交往频繁，信息交流流畅低廉，成员也相对稳定。这些特征使得合作均衡一旦在保护区社区形成，就有被锁定的倾向。然而，使合作规范弱化的因素也是存在的，特别是那些距离市场较近的农村和自然保护区，商品经济的大潮及市场经济的思维冲击着每一个农民，从而导致农民越来越像“经济人”。不仅如此，农民还会受到各种各样随机因素的冲击，这些随机因素可能是他们缺乏信息、受到短暂压力带来的。比如，2008年的5.12地震使得白水江自然保护区居民的房屋严重损毁，无论这部分村民开始是何种类型的，重建的压力可能迫使部分村民产生机会主义行为。因此，我们不禁要问：互惠主义构建的合作系统能抵挡住机会主义行为的侵扰吗？

直观上很容易证明，H₁是李亚普诺夫稳定⁽⁵⁾的，假设H₁中某个点受到一个小的扰动，这一扰动带来了一些机会主义行为，互惠者不少于群体的一半使得那些背离者不会通过剥削合作者而得到很多好处。特别地，他们的支付一定小于群体平均值，那么他们的频率会随着时间减小，而H₂中没有点是李亚普诺夫稳定的。

综合以上，我们的结论是：农民的互惠行为对于解决合作难题有着关键性的作用，然而互惠群体的比重对于合作博弈的均衡及其稳定性都有着重要影响，初始较高的互惠群体比例将通过复制动态机制消除对合作有害的机会主义行为，并且可以抵制某种程度的冲击。