一个制度选择的演化博弈模型

二、一个制度选择的演化博弈模型

在一个2×2的博弈模型里，存在两个博弈方，他们面临的选择有两个：一个是社区的本土制度，另一个是国家提供的正式规则。他们的策略组合和利益情况如下：

表10-1　囚徒困境：收益（行，列）

当博弈双方A和B都采用本土规则时，他们得利为a（a>0）；当A和B都采用正式规则时，获得的收益为b（b>0）；当A采取本土规则，B采取正式的规则时，则他们的得利分别为b和c；反之亦然。

假设在一群体中，采用本土规则策略的比例为x，采取国家强制性规则的比例为（1-x），那么据演化博弈模型，博弈双方的期望所得分别为：

u_A=xa+（1-x）b，u_B=xc+（1-x）d

整个群体的期望收益为：

根据复制动方程，有：

令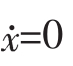，得到复制动态的稳定状态点，它们分别是：

演化稳定策略必须满足的条件是：

F（x^*）＝0，F′（x^*）＜0

讨论：

1）当a>c，b>d

即双方采取同样策略所获得的收益大于双方采取不同策略的收益，将x^*分别代入得到：

由此可知，博弈的稳定状态点是x^*₁=0和x^*₂=1，具体见下图：

当a>c，b>d时的演化博弈均衡

根据以上复制动态相位图可知，当初始的x位于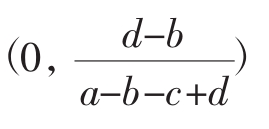时，所以博弈方最终将采取本土策略；当初始的x位于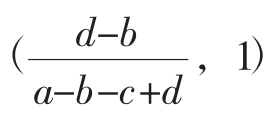时，所有博弈方最终将采取国家的正式规则。最终博弈双方会采用哪种策略取决于初始状态以及a与c、b与d的大小。

2）第二种情况：当a<c，d<b时

即本土规则的得利比正式规则策略小，将x^*分别代入得到：

由此可知，博弈的均衡状态点位：

当a＜c，b>d时的演化博弈均衡

3）第三种情况：a>c，d＜b

也就是不管对方的策略如何，采取本土规则的获利总比正式规则的大。将x^*₃分别代入得到：

F′（0）＞0，F′（1）＜0，x^*₃＜0或x^*₃＞1（与0≤x≤1矛盾，故舍去），由此可知，稳定点是x^*₂=1，既不管初始状态如何，经过多次博弈，所有参与人都演变成本土规则采纳者。见下面的相位图：

当a>c，b>d时的演化博弈均衡

4）第四种情况：a＜c，d>b，也就是不管对方的策略如何让，采取本土规则的获利总比正式规则的大。将x^*分别代入得到：

F′（0）＜0，F′（1）>0，x^*₃＜0或x^*₃>1（与0≤x≤1矛盾，故舍去），由此可知，稳定点是x^*₁=1，既不管初始状态如何，经过多次博弈，所有参与人都演变成正式规则采纳者。见下面的相位图：

当a＜c，b＜d时的演化博弈均衡