产销不平衡问题的运输规划

子任务3.2　产销不平衡问题的运输规划

3.2.1　任务引入

【任务3-2】　求解表3-42所示运输问题。

表3-42

3.2.2　任务分析

前面所讲的表上作业法的计算与理论，都是以产销平衡，即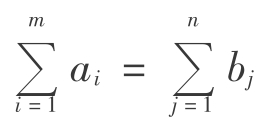为前提的。但在实际问题中产销往往是不平衡的。为了用表上作业法计算，就需要把产销不平衡的问题转化为产销平衡的问题。

当产大于销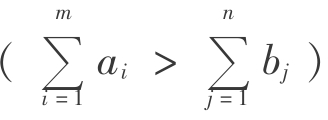时，运输问题的数学模型的表格形式可以写成如表3-43所示。

因为产量大，销量小，所以销地需求量都能满足，列约束为“=”；而产品不一定全部运出去，故行约束为“≤”。现在增加一个假想的销地（实际上是库存）B_n+1，该销地总销量为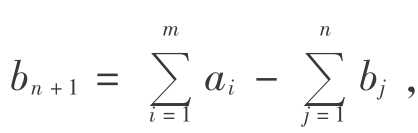由于是假想的销地，实际上没有调运，故其单位运价为c_i，n+1=0，设运量为x_i，n+1（i=1，2，…，m），将其列入表3-43的B_n列后，得表3-44。

表3-43　运输问题的表格模型

表3-44　加入虚销地的运输问题

由于虚设了销地B_n+1，故行约束变为了“=”，注意到x_1，n+1+x_2，n+1+…+x_m，n+1=b_n+1，所以第n+1个列约束也变为“=”。这样表3-44就转化为一个产销平衡的运输问题。我们可以按前面介绍的方法求解。

3.2.3　任务实施

求解表3-42所示运输问题。

步骤一　建立模型

因为总产量（15+18+17=50）＞总销量（18+12+16=46），所以这是一个产大于销的问题。

虚设一个销售地B₄，其销量为产销之差，即b₄=50-46=4，在表3-45中增加B₄一列，该列的变量x_i4（i=1，2，3）表示就近存储在原产地的多余产品的数量，而非真实运量，因此该列运价全为0，这样就把该问题化成平衡问题了。

步骤二　用表上作业法进行运输规划

用最小元素法确定其初始方案，用闭回路法求其检验数，结果见表3-45。

步骤三　求出检验数，判别方案是否最优

表3-45

步骤四　方案的调整

用闭回路法进行调整，又得一个新方案，见表3-46。经检验该方案为最优方案。

最少总运费为S=116。

表3-46表明：产地A₃有4个单位货物存储在仓库里。

注意：该例在用最小元素法确定初始方案时，尽管虚设的销地B₄列的运价全为0，均为最小，但我们先不考虑它，而先给有实际运输任务的其他产销地之间安排运量，最后才给B₄列安排运量。对产销不平衡的运输问题采用这样的处理方法，往往能够获得较好的初始方案，从而减少调整次数。

表3-46

当销大于产时，即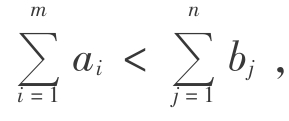类似地，我们虚设一个产地A_m+1，其产量a_m+1为销量与产量之差，即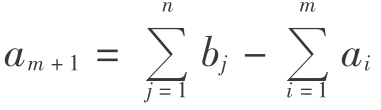，单位运价为c_m+1，j=0（j=1，2，…，n），这样就转化为产销平衡问题，可按前面介绍的方法进行求解。