资源分配问题的实际应用

子任务4.4　资源分配问题的实际应用

4.4.1　任务引入

【任务4-4】　某公司拟将500万元的资本投入所属的甲、乙、丙3个物流中心进行技术改造，各物流中心获得投资后年利润将有相应的增长，增长额见表4-18。试确定500万元资本的分配方案，以使公司总的年利润增长额最大。

表4-18

4.4.2　任务分析

所谓资源分配问题，就是将一定数量的一种或若干种资源（如原材料、机器设备、资金、劳动力等）恰当地分配给若干个使用者，或投资于几家企业，以获得最大的效益。设有m种资源，总量分别为b_i（i=1，2，…，m），用于生产n种产品，若用u_ij代表用于生产第j种产品的第i种资源的数量（j=1，2，…，n），则生产第j种产品的收益是其所获得的各种资源数量的函数，即g_j=f（u_1j，u_2j，…，u_mj）。由于总收益是n种产品收益的和，此问题可用如下静态模型加以描述：

当g_j=f（u_1j，u_2j，…，u_mj）是线性函数时，该模型是线性规划模型；当g_j=f（u_1j，u_2j，…，u_mj）是非线性函数时，该模型是非线性规划模型。此模型用线性规划或非线性规划来求解都将是非常麻烦的。然而在此情况下，由于这类问题的特殊结构，可以将它看作一个多阶段决策问题，并利用动态规划的递推关系来求解。

本教材只考虑一维资源的分配问题，设状态变量S_k表示分配于从第k个阶段至过程最终（第N个阶段）的资源数量，即第k个阶段初资源的拥有量；决策变量u_k表示第k个阶段资源的分配量。于是由状态转移律：

S_k+1=S_k-u_k

允许决策集合：

D_k（S_k）=｛u_k｜0≤u_k≤S_k｝

最优指标函数（动态规划的逆序递推关系式）：

利用这一递推关系式，最后求得的f₁（S₁）即为所求问题的最大总收益。

4.4.3　任务实施

步骤一　分阶段建立模型

将问题按物流中心分为3个阶段k=1，2，3；

状态变量S_k（k=1，2，3）代表从第k个物流中心到第3个物流中心的投资额；

决策变量u_k代表第k个物流中心的投资额。于是有状态转移率S_k+1=S_k-u_k；

允许决策集合D_k（S_k）=｛u_k｜0≤u_k≤S_k｝

递推关系式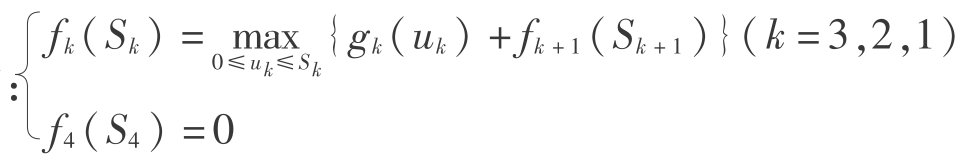

步骤二　递推过程

（1）当k=3时

于是有表4-19，表中u^* 3表示第三个阶段的最优决策。

表4-19　　　　　　单位：百万元

（2）当k=2时

于是有表4-20。

表4-20　　　　　　单位：百万元

（3）当k=1时

于是有表4-21。

表4-21　　　　　　单位：百万元

步骤三　结论

然后按计算表格的顺序反推算，可知最优分配方案有2个：

①甲物流中心投资200万元，乙物流中心投资200万元，丙物流中心投资100万元；

②甲物流中心没有投资，乙物流中心投资200万元，丙物流中心投资300万元。

按最优分配方案分配投资（资源），年利润将增长210万元。

这个例子属于决策变量取离散值的一类分配问题，在实际问题中，相类似的问题还有销售店的布局（分配）问题、设备或人力资源的分配问题等。