验收抽样方案的操作特性和设计

第四节　验收抽样方案的操作特性和设计

一、抽样方案的操作特性

抽样方案的操作特性也称为抽检特性，是指抽样方案对交验批实际质量水平的鉴别能力。对于确定的抽样方案，如用它来对某个交验批作验收抽样检验，则将交验批判为合格因而接收是一随机事件，这一随机事件的发生概率称为抽样方案对交验批的接收概率，常用P_a来表示。抽样方案的操作特性可以通过其对不同质量水平的交验批的接收概率来反映。

接收概率是交验批实际质量水平的函数，这个函数称为抽样方案的操作特性函数（Operation Characteristic Function），简记为OC函数，函数的图像称为抽样方案的操作特性曲线（Operation Characteristic Curve），即OC曲线。OC函数和OC曲线是研究抽样方案操作特性的重要工具。

若交验批质量水平用批不合格率p来表示，则抽样方案对交验批的接收概率为Pa＝L（p）。当抽样方案对交验批的合格判定标准定为批不合格率p₀时，则理想的抽样方案应当以100%的概率接收批不合格率p≤p₀的交验批，即当p≤p₀时，P_a＝L（p）＝1；而以100%的概率拒收批不合格率p＞p₀的交验批，即当p＞p₀时，Pa＝L（p）＝0。像这样理想的抽样方案的OC曲线见图10－4。但是，实际抽样方案只能以高概率接收合格批，而以高概率拒收不合格批。若抽样方案合格判定标准为p₀（如p₀＝AQL），不合格判定标准为p₁（如p₁＝LTPD）。又若当p＝p₀时，抽样方案将合格批误判为不合格批的错判风险概率为α（即α＝PR），而当p＝p₁时，抽样方案将不合格批误判为合格批的错判风险概率为β（即β＝CR）。那么，抽样方案的OC曲线的大致形状如图10－5所示。

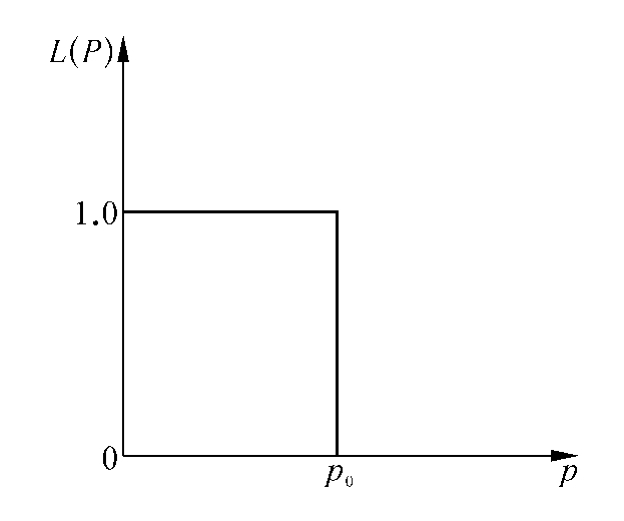
图10－4　理想方案的OC曲线

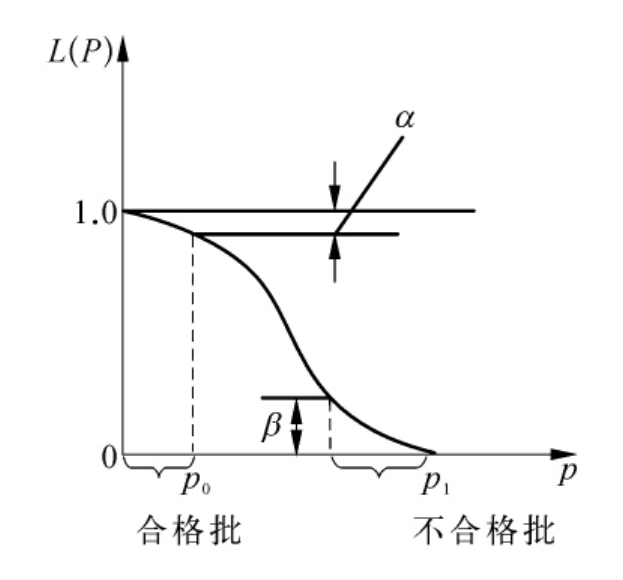
图10－5　实际方案的OC曲线

二、验收抽样方案的设计

（一）方案设计的一般原理

抽样方案其实是实施抽样检验时的一组规则，包括如何抽取样本、样本的大小以及批合格与否的判别标准。由于方案中样本个数一般在事先已经确定，所以，方案设计要做的事只是选择样本大小和判别标准。例如，对于图10－1所示的一次抽样，只需选择样本大小n和合格判定数C（Ac＝C；Re＝C＋1）；对于图10－2所示的两次抽样，只需选择两个样本的大小n₁和n₂，以及相关的合格判定数Ac₁和Ac₂及不合格判定数Re₁和Re₂（Ac₁＝C₁；Re₁＝Ac₂＝C₂；Re₂＝C₂＋1）。其他抽样方案的设计也类似。为了表达上的方便，常用符号（n｜C）表示上述一次抽样方案，用符号（n₁，n₂｜C₁，C₂）表示上述两次抽样方案。

方案设计时，为了使抽样方案能符合预期的性能要求，常见的方案参数约束有如下几种。

（1）合格质量水平AQL的约束：L（AQL）＝1－α。

（2）批最大允许不合格率LTPD的约束：L（LTPD）＝β。

（3）平均出厂质量极限AOQL的约束：AOQL＝p₁。其中p₁是事先确定的AOQL的限定值。AOQL能为用户提供明确的质量保证，是挑选型抽检方案设计时的重要参数约束。应用AOQL指标设计的典型的挑选型抽检方案，如美国的道奇—罗米格（Dodge－Romig）抽检表和日本的JIZ 9006还能使检验工作量减至最少的程度，因而特别适合企业内部的检验工作。

（4）使平均检验量ASN最小的约束。平均检验量ASN（Average Sampling Number）又常记作I，也是反映抽检方案性能的重要指标。对于多次抽样，只有当前一样本抽检结果无法对批质量是否合格作出判定时才需抽检下一个样本；对于挑选型抽样，只有当判定批质量不合格因而拒收时才需对整批产品实施全数检验。因此，多数检验方案实施时的实际检验量是不确定的。和操作特性函数一样，抽检方案的平均检验量也是交验批的实际质量水平的函数。

在抽检方案的设计中，可根据上述一个或几个约束条件来确定参数。当然，也可以考虑其他约束条件，但上述几个约束条件是最常使用的。当所给条件不足以确定方案参数时，也即有多种方案可供使用时，则需要比较它们各自的OC曲线，找出合乎理想的抽检方案。

（二）计数标准型一次抽检方案的设计

1．计数标准型抽检方案的特点

（1）为了对供需双方同时提供保护，方案参数必须满足如下约束：

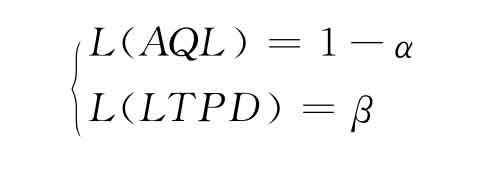
（2）不要求供方提供交验批验前资料，适用于对孤立批的检验。

（3）对破坏性检验也适用。

（4）不规定对拒收批如何处理。

（5）和提供验前资料或只保护供需双方某一方利益的抽检方案相比，如要求同等操作特性，所需抽检量较大。

2．（n｜C）方案设计的例子

应用中，为了方便，往往利用各种现成的方案表来确定参数n和C。

（1）J．M．Cameron抽检表。J．M．Cameron抽检表（见表10－3）规定和合格质量水平AQL对应的生产者风险PR＝α＝0．05，和批最大允许不合格率LTPD对应的消费者风险CR＝β＝0．10。相应地，在表中记AQL＝p_0．95，LTPD＝p_0．10。J．M．Cameron抽检表适用于样本中不合格品数服从泊松分布的抽样检验问题。当不合格品数服从二项分布或超几何分布时也可近似采用。

表10－3　J．M．Cameron抽检表

续　表

例1　如AQL＝p_0．95＝0．001，LTPD＝p_0．10＝0．01，求抽检方案（n｜C）。

解：由于p_0．10/p_0．95＝0．01/0．001＝10，查表10－3中p_0．10/p_0．95列，发现10．946和10最接近，故确定C＝1。

在C＝1行中，根据np0．95＝0．001n＝0．355，得n＝355，即采用方案（355｜1）。此方案相应的p_0．10＝3．890/355＝0．011。

同样，在C＝1行中，根据np_0．10＝0．01n＝3．890，得n＝389，即采用方案（389｜1）。此方案相应的p_0．95＝0．355/389＝0．000 9。

方案（355｜1）和（389｜1）都能基本满足问题要求。虽然两者的操作特性存在微小差异，但实际应用中是可以忽略的。为了节约检验工作量，可以考虑选择方案（355｜1）。

（2）JIS－2－9002。JIS－2－9002是日本工业标准，由计数标准型一次抽检表（见表10－4）和抽验设计辅助表（见表10－5）组成。表10－4中，p₀（一般为合格质量水平AQL）栏分21个区段。p₁（一般为批最大允许不合格率LTPD）栏分17个区段。设计方案时，可能会遇到下列四种情况。

①在p₀行和p₁列交叉格上有方案，则该方案即为所求方案。

表10-4　计数标准型

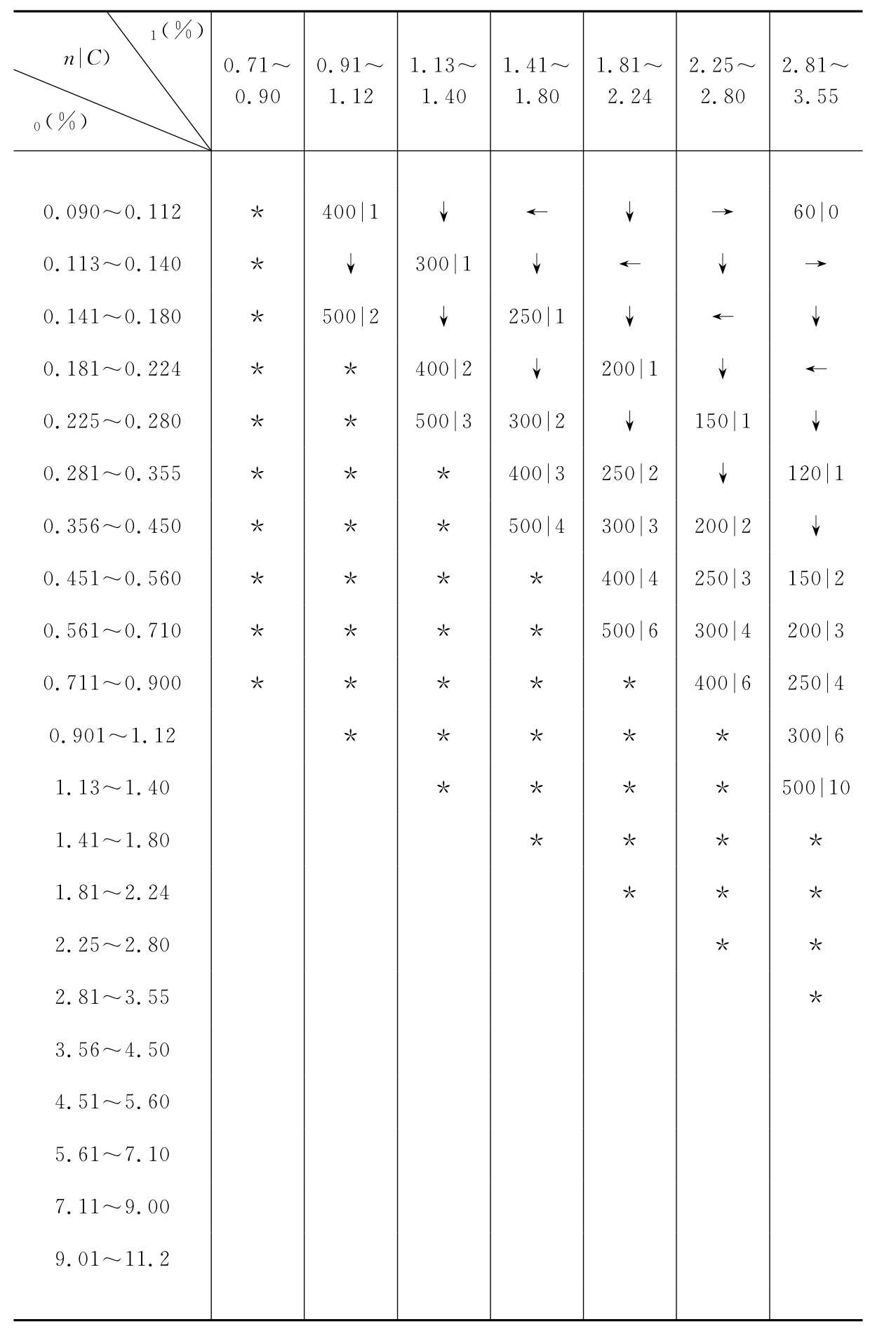
一次抽验表

②在上述交叉格上是箭头，则沿箭头方向寻找，首先遇到的方案格上所列方案，即为所求方案。

③按上述方法寻找方案，若找到的是“＊”号，则采用表10－5设计方案。

表10－5　抽验设计辅助表

备注：p₁/p₀＝1．86时，算出的n值非常大，失去了抽验的意义，故未列入表内。

④根据p₀和p₁值，表10－4中对应的是空格，则表示没有相应的计数标准型一次抽检方案（因为此时的p₀＞p₁，不合理）。

采用表10－5设计方案时，若n值非整数，则取最接近的整数；若n太大，如n≥N，则意味着应实行全数检验。

JIS－2－9002还附列了方案的OC曲线，可用来确定抽检方案的两类风险概率α和β。

例2　采用JIS－2－9002，确定例1所要求的抽验方案（n｜C）。

解：在表10－4中，p₀＝0．001＝0．1%属于（0．090%～0．112%）行，p₁＝0．01＝1%属于（0．91%～1．12%）列。行列交叉格处为方案格，所示方案（400｜1）即为所求的计数标准型一次抽验方案。

方案（400｜1）和例1中所得的方案（355｜1）及（389｜1）相比，三个方案都能满足问题的要求，但它们的操作特性略有差别。

例3　求p₀＝0．003，p₁＝0．05所对应的抽检方案（n｜C）。

解：在表10－4中，（0．281%～0．355%）行和（4．51%～5．6%）列的交叉格处为箭头“←”。在“←”左边为“↓”，在“↓”下方为方案格，所示方案（100｜1）即为所求。

例4　求p₀＝0．02，p₁＝0．04所对应的抽检方案（n｜C）。

解：查表10－4，对应的交叉格为“＊”，故需利用表10－5设计方案。

由于p₁/p₀＝0．04/0．02＝2，在表10－5中，属于（2．2～2．0）行，故C＝15，而n＝（502/0．02）＋（1065/0．04）＝51725。因此，所求方案为（51725｜15）。

方案（51725｜15）中样本实在太大，这是由于p₀和p₁过于接近所造成的。当遇到这样的情况时，可能需要对原定的AQL＝p₀和LTPD＝p₁是否合理进行研究并作适当调整。