新古典增长模型的基本框架

二、新古典增长模型的基本框架

索洛新古典经济增长模型建立在如下假定的基础上，其中包括：

（1）该经济社会只生产一种产品，这种产品既能作为消费品，也能作为投资品。

（2）生产过程中使用两种生产要素，劳动和资本，且劳动和资本可以在一定范围内替代，资本—产出比率可以变化。

（3）生产函数满足规模报酬不变条件，但要素的边际产量递减。

在这些假定下，我们考察均衡增长的基本条件。令y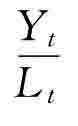_t＝、k_t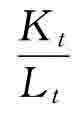＝，那么上述集约生产函数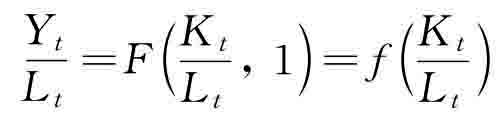，可以写成：

根据国民收入决定的基本理论，收入取决于计划投资和计划消费，将均衡条件两边同时除以劳动量，可得：

将人均资本k_t对时间t求微分，可得：

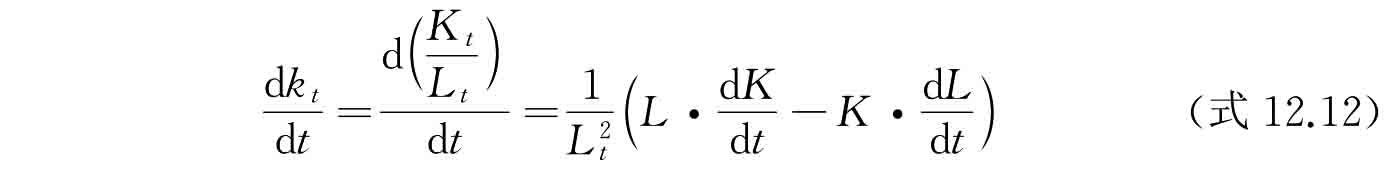
假设人口增长率恒为n，劳动力在人口中的比例固定，那么劳动力增长率也为n。

劳动力增长率n＝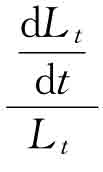

由于随时间变化资本的变化量就是投资，因此有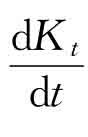＝ΔK_t＝I_t。

上式可写成：

把宏观经济均衡条件改写，可得：

由S_t＝sY_t及S_t＝Y_t－C_t，式12．13可以写成：

将式12．10代入，可得经济增长的基本公式：

式12．15说明了当宏观经济达到均衡时，储蓄转化为两类投资，一类称为资本的深化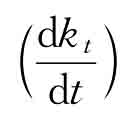，一类称为资本的广化（nk）。资本的深化意味着人均资本的增加，即每个劳动力都拥有较多的资本量。资本的广化是指为每一新增劳动力提供资本。如图12．5所示，图中横轴表示人均资本量，纵轴表示人均产出，f（k_t）为总量生产函数，sf（k_t）为储蓄函数，它表明了在任一人均产出水平，储蓄都是人均产出的s份额，从曲线上看，对应于每一人均产出水平，储蓄曲线都是生产函数向下移动1－s单位。在图12．5中，当人均资本量为k₁时，储蓄为sf（k₁），人均产出为y₁＝f（k₁），用于资本广化的数量为nk₁。

图12．5　索洛增长模型

那么，人均资本会如何变化呢？由索洛增长模型的基本关系式sf（k_t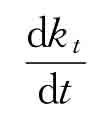）＝＋nk_t可以得到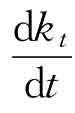：＝sf（k_t）－nk_t。

当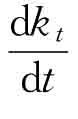＞0，即sf（k_t）＞nk_t时，意味着人均资本量在增加，如图12．5人均资本量为k₁时，人均产出除了用于消费外，储蓄量的一部分使资本广化，满足新增劳动力对资本的需求，同时还能够使资本深化，人均资本量提高。随着时间的变化，人均资本持续提高，直到达到k^＊。当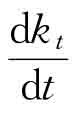＜0，即sf（k_t）＜nk_t时，意味着人均资本量在减少，如图12．5人均资本量为k₂时，人均产出除了用于消费外，储蓄量尚不足以满足资本广化的需求，人均资本量减少。随着时间的变化，人均资本持续降低，直到达到k^＊。

只有在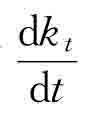＝0，即sf（k_t）＝nk_t，所有储蓄均用于满足新增劳动力的需求，人均资本不再进一步变化，经济在k^＊达到均衡，这时的人均产出为y^＊。

人均资本量为k^＊保持不变。因此，各变量的变化情况是：

（1）劳动力以n速率增长，资本也以n速率增长。这是因为，k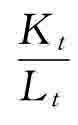^＊＝，即均衡状态下，L_t以n速率增长，而k^＊不增长，那么，资本量K_t也以n速率增长。

（2）人均产出不变，为y^＊，总产出增长率也为n，这是因为规模报酬不变，当劳动和资本均以n速率增长时，总产出当然也以n速率增长。

这时，当人口增长率不同时，不同nk_t曲线与sf（k_t）相交，每种情况下的交点都是均衡增长点，总产量的增长率等于人口增长率，而与储蓄率无关。