双寡头理论

7.3.2　双寡头理论

法国经济学家古诺在1838年《财富理论的数学原理研究》一书中最先提出一个相互竞争的双寡头市场模型，因此又称古诺模型。

古诺模型的假设条件很苛刻：①只有两个生产者，产品完全相同；②厂商的生产成本为零，这是为了分析的简单；③市场需求曲线是线性的；④各方根据对方的行动持续作出反应；⑤各方通过调整产量实现利润最大化。

图7－12　古诺模型

如图7－12，假设开始时市场上只有一家厂商A，那么这是一个垄断市场。根据垄断市场均衡条件MR＝MC可以得到厂商A的均衡产量。由于无成本生产，厂商A的均产量为OM₁，均衡价格为P₁。由于需求曲线为线性，边际收益曲线与横坐标得交点M₁必然位于ON点中间，OM＝1/2ON。

【经济学小贴士7－3】　垄断厂商的线性需求曲线与对应边际收益曲线的关系

当需求曲线为线性时，垄断厂商的边际收益曲线比需求曲线陡两倍。

证明：假设反需求曲线为P＝a－bQ，可得总收益函数

TR＝PQ＝（a－bQ）×Q＝aQ－bQ²

MR＝a－2bQ

边际收益曲线斜率为－2b，而反需求曲线收益为－b，因此得证。

当p＝0时，Q＝a/b；当MR＝0时，Q＝a/2b。边际收益曲线在横坐标截距是需求曲线在横坐标截距的一半。

现在另外一家厂商B也想进入该市场。目前市场只剩下M₁N的剩余产量，因此B厂商面对的剩余需求曲线是GN。B厂商根据MR＝MC原则生产，结果生产了剩余产量M₁N的1/2，即1/4ON。当B厂商进入市场并计划按1/4ON销售时，A厂商发现剩余的市场机会只有3/4ON，于是重新调整产量。根据MR＝MC原则，A厂商发现生产1/2×3/4ON产量，即3/8ON为最优选择。当A厂商确定产量后，B厂商重新审视新的剩余产量5/8ON，于是决定生产5/16的均衡产量。

这种调整过程不断反复，A厂商从原来的1/2ON不断萎缩生产，B厂商从进入的3/8ON不断增产。由于两家厂商成本相同，面对的需求曲线一致，因此调整直到两家厂商产量相等时才结束。那么是否他们平分了ON的总产量呢？

假设ON为T，我们先来看看A厂商产量的调整过程：

第一轮1/2T

第二轮3/8T　　　　　　减少了1/8T

第三轮11/32T　　　　　减少了1/32T

第四轮43/128T　　　　 减少了1/128T

……

A厂商的最终产量为

｛1/2－1/8－1/8×1/4－1/8×（1/4）²…1/8×（1/4）^N｝×T＝1/3T^[1]

同理，B厂商的产量调整结果也应该为1/3T。

【思考题7－1】　B厂商的调整过程是如何的，如何用数列求和？

因此古诺模型两厂商最终没有平分总需求，而是平分了总需求的2/3。这个产量是高于垄断均衡产量的，然而比竞争下的均衡产量要低。为了让读者深刻体会这种相互依存性，下面我们用代数方法再进行阐述。

假设两个寡头厂商共同面对的反需求函数为P＝a－bQ，成本C＝0（其中a＞0，b＞0）。A厂商产量为q₁，B厂商产量为q₂，Q＝q₁＋q₂。下面来看看A厂商的总收益状况：

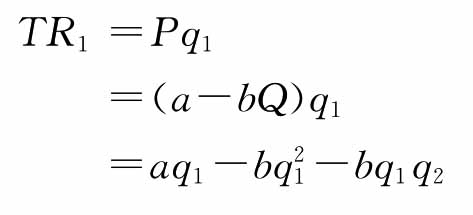
MR₁＝a－2bq₁－bq₂，因利润最大化的一阶条件是MR＝MC，且MC＝0，因此可得

a－2bq₁－bq₂＝0

同理得到厂商B的利润最大化一阶条件：

a－2bq₂－bq₁＝0

将两式联立

式（1）是厂商A的均衡条件，换句话说，它表述了厂商A面对厂商B不同产量决策时自己的产量变动方法，因此我们又把它称为厂商A的反应函数。那么式（2）就是厂商B的反应函数。如图7－13，R₁（q₂）、R₂（q₁）分别是厂商A、B的反应函数。

图7－13　古诺模型

R₁（q₂）上任何一点都表示厂商A对B产量决策作出的最佳反应，但却偏离了厂商B对A的最佳反应，因此这条线上的产量集合不稳定。R₂（q₁）上任何一点都表示厂商B对A产量决策作出的最佳反应，但却偏离了厂商A对B的最佳反应，因此这条线上的产量集合也不稳定。只有在两条线的交点E才是双方对彼此的最优决策，因此E点的产量集合才是稳定的产量均衡。

在E点我们分别得到。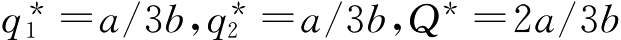

假设按成本价卖，市场的总需求量为T。根据反需求函数P＝a－bQ，由于厂商成本为零，那么P＝0时Q就是总需求量，Q＝a/b＝T。两个厂商平分了2/3T的总需求量，结论和前面相同。

【思考题7－2】　考虑推广到N个厂商，每个厂商的最优产量是多少？与N有关吗？