从数学文化谈数学与现代服务业人才培养实验教学的融合

从数学文化谈数学与现代服务业人才培养实验教学的融合

从数学文化谈数学与现代服务业人才培养实验教学的融合^[1]

张立卓

摘　要:本文探讨了数学文化在现代服务业人才培养实验教学中的素质教育功能。

关键词:数学文化;数学素养;现代服务业;人才培养

对现代服务业人才进行素质教育的着眼点之一是在大学教学中充分践行人文教育与科学教育的融合，培养既有人文素养又有科学精神、既懂得人文理念又掌握科学方法的高素质专业人才。而使更多的大学毕业生成为国家和社会的大用之材，正在成为越来越多教育工作者共同关心和探究的教育问题与文化问题。

一、数学与现代服务业人才培养实验教学融合的背景

一般的数学课，由于受教学时数的限制等原因，教师多半以讲授数学理论及其应用为主，对于数学在思想及人文方面的一些内容，例如数学史、数学家、数学思想、数学方法等这样一些基本的数学文化内容，涉及很少，很难有时间做系统介绍。因此尽管学生已经学了多年的数学课，但大多数学生对数学的思想、精神了解得依然很肤浅，对数学的宏观认识和总体把握较弱。而这些数学素养，恰恰是数学让人终生受益的关键因素。

如果将数学教学仅仅看成是知识的传授，那么即使包罗了再多的定义和定理，可能仍免不了沦为一堆死板的教条，难以发挥作用;而掌握了数学的思想方法和精神实质，就可以由为数不多的几个定理演绎出千变万化的生动结论，以显示数学无穷的威力和魅力。事实上对学生而言，在未来的工作(非数学领域)岗位中真正需要用到的数学定理和公式，其实不多，学校里学过的很多数学理论在今后的工作岗位上很多都似乎没有直接派上什么用场，有的甚至已经遗忘。然而，不管他们从事什么工作，所受的数学训练，所领会的数学思想和精神，数学的理性思维方式、研究方法、推理方法和看问题的着眼点等，却无时无刻不在发挥着积极的作用，成为走向成功的最有利的因素，使他们终身受益。

二、数学文化与数学素养

恩格斯指出:数学是研究现实世界中数量关系和空间形式的科学。顾沛先生指出:数学不仅是一种重要的工具或方法，也是一种思维模式，即“数学方式的理性思维” ;数学不仅是一组知识，也是一种素质，即“数学素质” ;数学不仅是一门科学，也是一种文化，即“数学文化”^【1】。

“数学方式的理性思维”包括形式逻辑的理性思维模式和辩证思维的理性思维模式。其中形式逻辑的理性思维模式保证了数学定理的精准性，辩证思维的思维模式则形成数学中的许多重要思想方法与精神实质。

“数学素质”也称“数学素养” 。“数学素养”的通俗说法是“把所学的数学知识都排除或忘掉后，剩下的东西” 。教育部高等学校“数学与统计学教学指导委员会”的项目结题报告——“数学学科专业发展战略研究报告”中指出“数学素养”包括以下五个方面:第一，主动探寻并善于抓住数学问题的背景和本质的素养;第二，熟练地用准确、简明、规范的数学语言表达自己数学思想的素养;第三，具有良好的科学态度和创新精神，合理地提出新思想、新概念、新方法的素养;第四，对各种问题以“数学方式”的理性思维，从多角度探寻解决问题的方法的素养;第五，善于对现实世界中的现象和过程进行合理的简化和量化，建立数学模型的素养。

“文化”是人类社会历史实践过程中所创造的物质财富和精神财富的总和、积淀。“数学文化”一词的内涵，是指数学的思想、精神、方法、观点，以及它们的形成和发展;广泛些说，除上述内涵以外，还包含数学家、数学史、数学美、数学教育、数学发展中的人文成分、数学与社会的联系、数学与各种文化的关系，等等。“数学文化”教育的宗旨就是提高学生的数学素养^【1】。

方延明先生指出:“把数学作为一种文化研究，在于它表现了一种前所未有的探索精神与创新智慧，它的理性思维的功能发挥得淋漓尽致，它给人提供的不仅仅只是理性思维模式，同时又是一种有力的解决问题的工具和武器，既反映了思维上的合理性和价值趋向，又拓展了人们的思想解放之路” ^【2】。

在数学教学中，介绍“数学文化”一方面注重数学思维方法的传授，对于普及数学知识、倡导数学方法、推崇理性思维、传播数学思想、弘扬数学精神，发挥了一般课程难以替代的素质教育功能;另一方面这种“渗透、嵌入”特别注重人文的精神和思维方法的传授，讲究科学与人文的融合，对培养学生树立正确的科学观，人生观以及价值观具有重要的指导意义。

三、“数学文化”在现代服务业人才培养实验教学中的素质教育功能

华罗庚讲:“宇宙之大，微粒之微，火箭之速，化工之巧，地球之变，生物之谜，日用之繁” ，可见数学无处不在。曾有学者指出:“一个国家的科学进步，可以用它消耗的数学来度量” 。可见数学作为一门基础学科，已经渗透到科学领域的各个方面，它的进步标志着一个民族科学文化素质的提高。人类社会的进步是以科学技术的传承与发展为第一生产力的，数学文化就是先进生产力。

(一) “数学文化”在现代服务业人才培养实验教学中的模型化功能

数学模型的最优之处是它舍弃了具体事物中的一切与研究目标无本质联系的各种具体的物质属性，其中所蕴含的是纯粹意义下的数量关系与空间形式。因此数学模型更具有普适性。任何一门科学，只有成功地建立数学模型基础上才称得上完善与纯熟。在当今世界，数学模型不仅仅是一种抽象的结构，更是人类改造与服务客观世界的武器与智慧结晶。例如，随机服务模型就是一个例子:

随着日常生活的高效率，高节奏，美发业处于市场激烈的竞争之中。如何吸引更多的顾客以获取更高的利润是每位老板最关心的问题。除了增加服务项目，提高品位，保证质量，降低成本外，理发店应在“快”字上下功夫。有人向老板建议，公开向顾客宣布:如果让哪位顾客等待超过一定时间，那么顾客可以免费理发。老板希望对于利弊有一定量的分析，比如作几分钟的承诺?利润能增加多少?应建立随机服务模型，给出解决这个问题的一种方法。

模型假设(1)顾客在理发店的服务服从M/M/1模型，顾客平均到达率为λ =1/c，c为平均到达间隔，在未宣布承诺时，c = c₀，理发店平均服务率为μ = 1/d，d为平均服务时间，d＜c。(2)店方承诺等待时间超过δ的顾客免费理发，δ越小则顾客越多，c越小。在一定范围内设c与δ成正比。同时存在δ的最大值δ₀，当δ≥δ₀时，理发店的承诺对顾客无吸引力。相当于不承诺，不妨设此时c = c₀。(3)每位顾客的理发费为p，成本为q。

模型建立由对M/M/1模型的分析，顾客等待时间Y服从参数为μ- λ的指数分布，其中μ =1/d，λ =1/c，即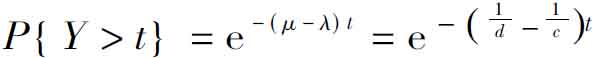 ，对于等待时间为Y的顾客，设店方获得的利润为Q(Y) ，则在宣布承诺时间为δ的情况下，有

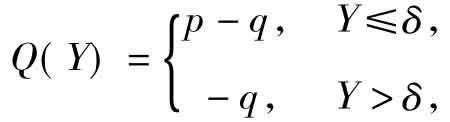
利润Q的期望值为E(Q) = (p- q) P{ Y≤δ}- qP{ Y＞δ} ，代入概率值得

由于顾客到达的时间间隔为c，所以单位时间利润的期望值为

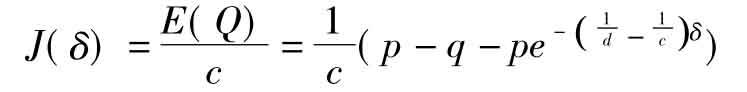
“以最小的投入，获得最大的利润” ，这是现代服务业所应追求的，特别是在大型服务工程上，当然要有一个最优化安排问题，否则有可能会因为协调不畅而损失人力，物力及财力。可见数学模型为现代服务业的可持续发展提供了强有力的理论框架基础。

(二) “数学文化”在现代服务业人才培养实验教学中的思想方法功能

1.“类比”的思想方法

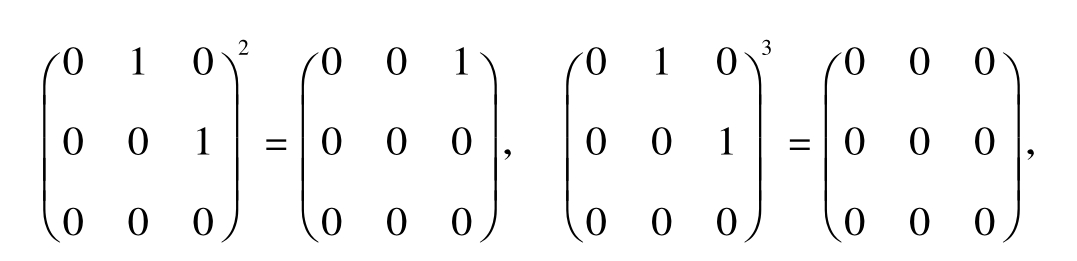
即要求X，使(E + B) X = E，因为即B³= O，也即相当于求矩阵X，使(E + B) X = E + B³，相比较数a，b，有

(a + b) (a²－ ab + b²) = a³+ b³，

类比可得(E + B) (E²－ EB + B²) = E + B³，从而X = E²－ EB + B²= E- B + B²=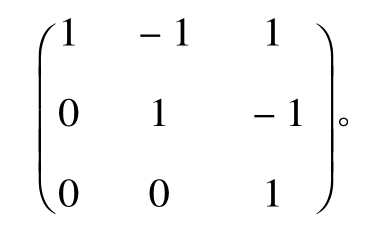

当然也可以利用逆矩阵求解X = A^－1。

2.“抽象”的思想方法

抽象是数学的一大特点。不仅数学概念是抽象的，而且有时数学方法也是抽象的。下面以哥尼斯堡七桥问题为例，来说明数学中的“抽象”的方法。

哥尼斯堡是欧洲一座美丽的城市，有一条河(普雷格尔河)流经该市，河中有两个小岛，岛与两岸间，岛与岛间有七座桥相连。如何不重复地走过这七座桥。欧拉思考后，首先把岛和岸都抽象成“点” ，把桥抽象成线。然后欧拉把哥尼斯堡七桥问题抽象成“一笔画问题” :笔尖不离开纸面，一笔画出给定图形，不允许重复任何一条线，这简称为“一笔画” 。需要解决的问题是找到“一个图形可以一笔画”的充分必要条件，并且对可以一笔画的图，给出一笔画的方法。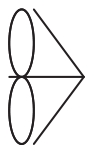

欧拉经过研究，完满地解决了上述问题。欧拉把图形上的点分成两类:注意到每个点都是若干条线的端点，如果以某点为端点的线有偶数条，就称此点为偶节点;如果以某点为端点的线有奇数条，就称此点为奇节点。欧拉得出了图形可以一笔画的充分必要条件:图形中的奇节点不多于两个。再由此看哥尼斯堡七桥问题，图形中有四个奇节点，因此不存在通过每条线一次且仅为一次的路线，该图形不能一笔画。由此欧拉揭开了拓扑学研究的序幕。

3.“化归”的思想方法

所谓“化归”是把未知的问题转化为已知的问题;把待解决的问题，归结为已解决的问题，从而解决问题的过程。比如在线性代数教学中，证明r(AB≤min{ r(A) ，r(B) }时就用到了这种思想方法。先借助矩阵分块法证明r(AB≤r(A) ，即积矩阵的秩不超过左矩阵的秩，接下来还需要证明积矩阵的秩不超过右矩阵的秩。此时采用化归的方法，将未解决的问题通过已解决的问题来化解。因为r(AB) = r(AB)^T≤r(B^TA^T)≤r(B^T) = r(B) 。(积矩阵的秩不超过左矩阵的秩) 。

4.“以有限驭无限”的思想方法

学生在中学阶段以研究常量为主，较多地用到“有限” ，在大学阶段以研究变量为主，较多地用到“无限” 。所以清楚有限与无限的联系与区别，是重要的数学素养。

有限与无限是有本质区别的。在无限集中“部分可以等于整体” ;对有限情形成立的命题对无限情形未必成立。但有限与无限是有联系的，比如通过考查前n项和的极限存在，可判定无穷级数收敛。当齐次线性方程组AX = O有非零解时，只需找到其含有限个解的基础解系，即求出其全部无穷多解，即体现了“以有限驭无限”的思想方法。

“数学文化”中蕴含着丰富的人文精神，在数学教学中介绍“数学文化” ，学生既可以把多年来学习的数学理论上升到思想、方法和精神的层面上，同时又可以从文化和哲学的角度反观数学发展的脉络与规律;既明晰了历史上的重大数学事件，又感受了数学家的情感、操守、品德和人生观;既感觉到社会进步对数学发展的推动作用，又认识到数学发展对社会文明与进步的促进作用。通过数学文化让数学与现代服务业人才培养实验教学有机的融合，是现代服务业人才素质教育深入开展的有效途径之一。

参考文献

［1］顾沛.数学文化．北京:高等教育出版社.2008.

［2］方延明.数学文化．北京:清华大学出版社.2007.

［3］顾沛.科学素质教育公共课中科学精神与人文精神的融合．南开大学报，2008.

［4］姜启源.数学模型．北京:高等教育出版社，1993.

【注释】

[1]本文为2010现代服务业人才培养实验教学创新论坛会议论文。