城区表层土壤重金属污染源定位及污染状况分析
吴 翟 芮 瑞 邵 俊
摘 要:本文研究人类活动影响下城市地质的环境演变。
对于问题1,我们将得到的数据录入MATLAB进行模拟作图,得到8种金属污染物的分布情况,同时用平均超标污染指数和总危害指数两种刻画标准,对5种城区的污染程度从污染物含量和生态危害两方面进行评价后得到的各区域污染程度由高到低依次为:工业区、交通区、生活区、公园绿地区、山区。
对于问题2,我们根据问题1中所得的8种元素的空间分布图,抓住每种元素在城区中的分布特点,结合实际经验与背景知识得出8种元素污染的原因:As,Cr,Cu,Hg,Ni,Pb,Zn污染可由工厂排污引起; Cd,Pb污染可由交通区车辆等因素引起; Cr,Cu,Hg,Ni,Pb,Zn污染可能由生活区垃圾集中处理引起。
对于问题3,我们通过结合问题1、2种得出的空间分布和污染成因,根据污染源的形态,确立了两种传播特征。线形污染源的两旁扩散式传播和点形污染源的中心聚集,四周缓慢扩散式的传播。此后,我们根据点形污染源的传播特点,建立统计回归模型,通过函数拟合确立污染源处的污染物含量与平面坐标间关系,最后通过建立最优化模型,通过找出污染源周围区域内函数最大值,确定污染源方位。
对于问题4,我们认为问题3中我们的模型便于操作,也比较符合所给的客观数据。但是我们通过加入大气模型与重金属土壤中运移模型进一步完善了研究城市地质环境的演变模式的数学模型。
关键词:重金属污染;统计回归模型;优化模型;高斯实用大气扩散模型;函数拟合
一、问题的重述
随着经济的发展与人口的膨胀,人类的活动对城市的环境造成了越来越大的影响,而研究人类活动影响下城市地质环境的演变也愈发地为人所重视。
现今的城区一般可按功能划分为生活区、道路区、山区、主干道区及公园绿地区等区域并可将之标号为1区至5区。人类活动对不同区域的地质环境的影响程度不同。
现考察某城区并将其划分为间距1公里左右的网格子区域,按照每平方公里1个采样点对0-10厘米深度的表层土进行取样、编号,同时记录采样点的坐标方位。此后获取每个样本空间内所含多种化学元素的浓度。此外,按照2公里的间距在那些远离人群及工业活动的自然区取样,将其作为该城区表层土壤中元素的背景值用以参照样本化学元素浓度。
现需要通过数学建模来完成以下任务:
(1)通过已有数据,给出8种主要重金属元素在该城区的空间分布,并藉此分析该城区内不同区域重金属的污染程度。
(2)通过数据分析,说明重金属污染的主要原因。
(3)分析重金属污染物的传播特征,通过建立模型,确定每种重金属污染源的位置。
(4)分析所建模型的优缺点,为更好地研究城市地质环境的演变模式,还应收集什么信息?结合新信息,建立模型解决问题。
二、问题的分析
(一)问题1的分析
问题1分为两个小问,首先第一问旨在已知城区各功能区内各样本8种重金属元素浓度的情况下,要求借此得出此8种元素在全城区的分布情况。通过对题目的了解,我们对此题作如下分析:
对土壤取样时,已将城市划分为间距为1平方公里的若干子区域,样本分布均匀、全面,可覆盖全城区,为导出重金属在全城区的分布提供了前提。
样本面积为1平方公里,相对于城市面积而言,样本面积较小,所得样本中测得的重金属浓度可相对精确的体现该样本区域内的平均浓度。
由于样本区域连续且密集,可以用相应的描点发并加以相应的模糊光滑处理,得出较精确的8种重金属元素在城区内的空间分布。
通过以上分析,我们可通过相关的数据处理及画图软件,结合现有数据,分别得到8种元素在全市区的空间分布。
对于第二个小问,它要求我们根据附件中所得数据以及第一小问中所得的8种重金属的空间分布,以一定的标准,综合判定各个城市区域中的重金属污染程度。针对此问题,我们作如下分析:
由于各个重金属数据所对应的单位名称各不相同,所以单纯的数值比较意义不大。
对某一区域的污染程度判定应结合题目附件中所给的背景值进行对比,进而得出各重金属元素的超标程度。
从生态学角度上讲,各个重金属元素的超标程度并不能作为判断超标程度的严格标准,各重金属对环境以及人体健康的危害程度各不相同,应对各种重金属的危害加以区分,并以最终的危害程度大小来判别不同地域的污染程度。
综上,我们决定通过样本测量值与背景值作比来确定每个样本点每种重金属的超标比例,进而确定每种区域中各种元素超标的平均值。通过该平均值,计算每个区域的污染超标指数,以此为标准进行比较。此外,我们还通过查找资料以及多方面的综合分析,确定每种重金属的危害程度并将其量化为毒性系数。在每一区域中,将每种元素的平均超标指数与其相对应的毒性系数相乘后加和,得出此区域的重金属元素总危害指数,通过对总危害指数进行比较来确定各区域的污染程度。
(二)问题2的分析
问题2要求我们分析重金属污染产生的主要原因。根据此问题,我们进行如下分析:
(1)污染生产者对其所生产的污染物分布有特殊影响。
(2)分析特殊影响在重金属元素空间分布上的表现,借此确定相符的区域。
(3)分析相应区域的城区分类,根据城区的分类以及该类城区功能特点,查找可能的污染成因。
(三)问题3的分析
本问题分为两个问题,首先需要我们确定污染物的传播特征。对于不同的污染物及成因,污染物的传播呈不同的特征。对于污染物的传播特征,我们的分析如下:
污染物的聚集方式与传播特征相关,现有聚集方式是传播作用后的结果。
污染物的传播特征与该污染物的起源有关,起源相近的污染物往往传播特征相近。
对于第二个问题,我们需要得出每一种污染物的污染源。通过对污染传播特征的分析我们可以将污染物的传播分为沿道路向道路两旁传播和中心向外传播两种方式。前者我们人为其传播服从高斯分布,后者我们可以根据相应的数据建立统计回归模型,得出相应污染源的污染传播函数,最后通过建立最优化模型得到污染物含量最高点的坐标,确立污染源。
(四)问题4的分析
本问题旨在要求我们对第三题的模型进行改进以达到更好地研究城市地质环境演变的目的。针对这个要求,我们做了如下分析:
(1)问题3中所作模型可以方便简单地刻画当前城市的地质环境情况,但考虑的因素仍有欠缺,需进一步改进。
(2)可尝试在模型中加入大气扩散对重金属污染物浓度分布的影响
(3)可尝试在模型中加入金属污染物在土壤层内部的扩散运动对金属污染物浓度分布的影响
三、模型假设
1.污染源对污染物的排放连续、均匀、稳定。
2.忽略城外地区污染源及污染物对城内地质环境的影响。
3.忽略城市内部各区原始地质中重金属含量的差异。
4.忽略城市上层空气对流、扰流对重金属污染物沉降的影响。
5.假设对全城区各样本空间进行采样结果均客观、真实,未受偶然因素干扰。
6.假设不同污染源间重金属的排放相互独立。
7.假设同一污染源对不同种重金属的排放相互独立。
8.假设重金属污染物在传播过程中不发生化学反应等变化。
四、定义与符号说明
1.cx表示任意采样点任意一种金属污染物浓度。
2.c0表示运算中元素对应的背景浓度。
3.cji表示任意采样点第j种元素超标污染系数[1]。
4.cj表示某区域内第j种元素的平均污染超标系数。
5.pj表示第j种元素的毒性系数。
五、模型的建立与求解
(一)问题1
1.8种主要重金属元素的全市分布情况
2.对该城区内不同区域重金属的污染程度的研究
(1)通过平均超标污染指数进行刻画
第一步:求出每个采样点每种元素的超标程度。即用采样的浓度值cx除以作为参照的同种元素背景浓度c0,得到相应的超标污染系数cki= cx÷ c0。
第二步:分别求出每个区域8种元素的平均超标污染系数,即cj=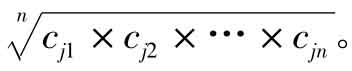 其中c为该区域内每采样点j编号所代表元素的超标污染jn系数。
其中c为该区域内每采样点j编号所代表元素的超标污染jn系数。
第三步:求出每个区域的总平均超标污染系数。即 其中c1至c8为区域i中8种元素的平均超标污染系数。
其中c1至c8为区域i中8种元素的平均超标污染系数。
第四步:比较数值PAi的大小,确定污染程度。经计算5个分区污染程度分别为:
生活区PA1 = 1.833 561 244;工业区PA2 = 2.348 448 408;山区PA3 = 1.067 862 907;
交通区PA4 =1.920 920 706;公园绿地区PA5 =1.577 990 14
综上:各区域污染程度由高到低依次为:工业区、交通区、生活区、公园绿地区、山区。
(2)通过总危害指数进行刻画
第一步:同(1)中的第一步与第二步。
第二步:通过查找资料,确立每种重金属元素对生态环境的毒性系数pj如下[3]:

生活区PB1 = 177.271 256 3;工业区PB2 = 289.453 181 4;山区PB3 = 101.396 923 9;交通区PB4 =202.072 305 1;公园绿地区PB5 =164.496 126 9
综上:各区域污染程度由高到低依次为:工业区、交通区、生活区、公园绿地区、山区。
(二)问题2
分析重金属污染的主要原因,我们选择从已获得数据和问题1中确立的各污染物空间分布,结合相关的背景知识,进行污染来源的确定。我们分析认为,山区由于海拔高度较高,且受人类活动影响较小,污染物浓度最低,成为污染原因的可能性微乎其微。同理,从公园绿地区的低污染物浓度以及公园的社会作用的角度看,公园绿地也可以排除成为大范围重金属污染来源的可能。以下是我们对8种元素污染原因的具体判断:
As
通过运用MATLAB对附件中的数据进行数据处理得出的空间分布图,我们发现虽然As污染在全市范围内都有分布,但在个别区域中污染程度急速上升至极高水平,峰值水平达到其他地区的6倍以上,说明As在这些区域中高度富集。而通过对这些富集区域的As污染浓度进行分析,我们认为此浓度水平已大大高于人类日常生活制造污染的水平,而在城市的各功能区域中,只有工业生产有能力使某一集中区域的污染物大量富集。所以我们认定砷污染的原因主要为城市中某些特定区域工厂的集中排放。
Cd
根据附件中Cd的数据以及空间分布图,我们可以发现镉在市区内污染浓度普遍较高,并没有出现高度集中富集的区域,而存在若干分布较规律、污染物浓度相对较高的区域,在空间分布图中表现为若干彼此相连的波峰区域。我们分析认为,镉污染没有集中的富集点,而其污染浓度较高的地区有彼此连续,通过对这些点的坐标进行定位,我们认为这些富集点大多存在于道路区。我们认为交通区污染的主要特点应为污染源连续,污染物主要向道路两旁扩散,污染物区域富集程度不及工业污染。这些特点与Cd污染的特点十分相似,所以我们认为Cd污染的主要原因是交通区汽车尾气的排放。
Cr
结合Cr的污染浓度数据以及空间分布,我们发现全城Cr污染物的分布除在一个较小的接近坐标原点的区域内高度密集分布外,在全城其他地区分布十分平均且与富集点的污染水平差距巨大最高点为平均值的19倍左右,所以基本可以排除工业生产之外的可能,所以我们认为Cr污染的主要原因为工厂废料的集中密集排放。
Cu
通过观察由Cu浓度取样数据模拟的Cu污染物浓度分布图,我们不难发现Cu污染同样仅仅密集集中在靠近坐标原点的一块区域内,峰值高出平均值45倍左右,其他地区浓度较低且差异不大,我们认定Cu污染的原因同样源于工业区的废物排放。
Hg
Hg浓度的空间分布展现出三个浓度远高于其他地区的Hg浓度富集点,三者峰值较其他地区平均值高出130倍左右。除三个富集点外的区域Hg浓度较低且分布均匀。三个浓度富集点连线的中点附近区域以及三点所构成三角形的几何中心区域的Hg浓度较低,借此我们可以判断Hg的三个富集点相互独立。Hg污染的原因应为三个浓度富集点附近的三个工业区排放废料造成。
Ni
通过分析Ni的样本测量值及其空间分布,我们可以发现在靠近坐标轴原点位置Ni元素出现了集中富集的情况,浓度值远高于城区的其他位置。我们分析Ni元素产生污染的原因同Cr等元素相类似,来源于工厂的集中排放。
Pb
通过对Pb的样本测量值进行分析并观察Pb的浓度的空间分布图,我们认为Pb集合了Cd、Cr两种元素浓度分布的特点。在靠近坐标原点的地区,存在一个大量富集Pb污染物的区域,Pb浓度远高于城市其他地区达7倍左右。但在城市的其他地区,仍相对密集、规则分布着连续的Pb浓度较高的区域,与城市的交通区域位置近似,所以我们推断Pb污染产生的原因分为两个方面,工厂的大规模集中排放,以及交通区汽车尾气的排放。
Zn
通过对Zn的样本测量值和MATLAB的图像,可以发现Zn污染物在全市主要分布在若干个富集点上,而在其他地区的Zn污染物浓度较低。通过计算,我们发现Zn在富集点的平均浓度是其他地区平均浓度的近11倍。所以我们认定Zn污染是通过若干区域中的工业区排放造成的。
此外,经过对8种元素的分析我们发现,在靠近坐标原点处的区域,多种元素产生富集。对于这些富集产生的原因,我们倾向于认为是该地区有工业区进行多种污染物的排放,但应该注意的是,若在该地区存在大规模的生活垃圾填埋场,用来填埋多方汇集的生活垃圾,也会产生相应的重金属元素富集现象。所以对于这些重金属元素污染的原因,也可能是有大规模垃圾填埋场的存在。
(三)问题3
1.关于重金属污染物传播特征的分析
对于重金属的传播特征我们利用题目附件中所给的样本点的浓度信息以及MATLAB的各重金属元素的模拟空间分布图进行分析,通过统计归纳,我们主要将重金属的传播特征划归为两种。
第一种:当污染源为线源时,污染物的传播特征是以线源为中线,向线源两端均匀传播,如Cd、Pb。在问题2中,我们判断Cd、Pb的污染原因为汽车尾气,那么这两种重金属元素的污染源就为交通区的道路线,即我们所说的线源。因此Cd、Pb两种元素浓度的峰值应该出现在城市交通区附近,随后其浓度沿向道路两侧的方向随距离的增大而依次递减。从图像上看,Cd、Pb两种元素的浓度都在交通区连续出现若干峰值,而交通区两侧的区域中,浓度随采样点距交通区距离的变大而减小,印证了我们的判断。
第二种:当污染源为点源时,污染物的传播特征为中心聚集,向外缓慢辐散。若重金属污染物的污染源为点源,则在污染源地区,污染物浓度出现最高峰值,由于重金属污染物在土壤中的传播速度较慢,所以当采样点距污染源距离逐渐增大时,土壤中重金属含量下降明显,当距离增大到一定程度时,该污染源对采样点的直接影响将可忽略不计,土壤中的重金属含量在一个较低水准保持恒定。通过对相应污染物空间分布的分析,我们发现,污染源为点源的元素分布空间中,总会出现若干区域,其污染物浓度峰值远远高于区域外的平均水准,而此区域的面积则往往十分有限,印证了我们的判断。
此外,我们还分析了海拔高度对污染物传播的影响。对于海拔高度相近的区域,海拔的影响对于污染物的传播并不明显,而当海拔差异明显时,污染物浓度的差异较为明显,高海拔的山区各种污染物浓度均明显低于低海拔地区。对此我们的理解是一方面高海拔的山地人类活动比较少,产生的污染也较少;另一方面我们认为高海拔的地势对于重金属元素在土壤中的传播的确可以起到一定的阻碍作用。
2.污染源位置的确定
(1)模型的建立
对于只具有第一种传播特征的元素,其污染源为单纯的线源,无法定位单一的污染源。对于具有第二种传播特征的元素,我们可以建立数学模型来推导出污染源的具体坐标。根据我们对第二种传播特征的理解,我们将污染物在某一方向向量上的传播方式简化为类似于二维的反比例函数模式(如下图) ,其中z轴表示污染物浓度,o点为污染源,x表示该方向上采样点距离污染源的距离。当污染物浓度无限趋近于无穷大时,x点的坐标就无限趋近于污染源位置。根据这个思路,我们将符合第二种传播特征的元素空间分布根据其出现峰值的情况,划分不同的污染源区域,在区域中找到题目中所给的相应的取样点,建立统计回归模型[4],通过1stopt软件函数拟合得到相应的空间函数。此后,根据划分的区域范围建立最优化模型[5],确立在该区域内取得最大值即无限逼近无穷大点的坐标即为所求污染源点坐标。
(2)问题的求解
①As污染源区域的划分:
区域1范围:11 000≤x≤14 000, 2 000≤y≤4 500
区域2范围:17 000≤x≤20 000, 9 000≤y≤12 000
模型建立及函数拟合求解
区域1:拟合函数为
Z(x, y) =(76 450 404.259 840 5 +794.812 120 099 298·x-
59 155.216 237 727 5·y +10.176 325 434 298 9·y2) ÷
(1 +190.396 069 735 052·x +4 413.896 545 669 99·y-
3.759 326 760 026 6·y2+0.000 674 159 107 200 694·y3)
趋近无穷点坐标为
X:11 002.431 582 727 4
Y:3 329.821 518 642 74
区域2:拟合函数为
Z(x, y) =(14 683.420 876 175 2-1.530 975 441 521 86·x +
6.614 750 025 975 25 ×10-5·x2-1.904 447 948 912 29·y +
0.000 103 310 860 915 178·y2) ÷(1 +0.177 867 346 683 019·x-
0.665 794 366 494 183·y +3.429 406 650 114 97 ×10-5·y2)
趋近无穷点坐标为
X:18 065.883 278 359 3
Y:9 000.016 749 327 96
②Cd污染源区域的划分
根据之前问题的分析,我们认为Cd只具备线源的传播特征,其传播源为城市交通区道路路线。
③Cr污染源区域的划分
区域范围:3 000≤x≤5 500,4 000≤y≤6 500
模型建立及函数拟合求解
拟合函数为
Z(x, y) =(30 912 243.266 340 9-20 049.188 301 206 9·x +
4.318 189 324 945 05·x2-0.000 307 151 190 924 119·x3-
57.100 137 155 969 4·y) ÷ (1 +2.405 246 802 781 39·x-
0.000 426 759 173 032 508·x2-0.474 851 219 970 848·y)
近无穷点坐标为
X:4 106.935 743 379 44
Y:5 646.148 962 478 08
④Cu污染源区域的划分
区域1范围:1 000≤x≤3 500,2 000≤y≤5 000
区域2范围:2 000≤x≤5 000,3 500≤y≤7 000
模型建立及函数拟合求解
区域1:拟合函数为
Z(x, y) =(-187 036.164 683 688 +173.167 605 351 131·x-
0.024 627 783 963 095 5·x2-22.995 828 239 185 6·y) ÷
(1 +0.648 387 395 796 509·x-0.537 157 877 464 48·y +
3.209 064 238 829 97 ×10-5·y2)
趋近无穷大点坐标为
X:1 545.558 238 599 63
Y:2 141.413 155 428 55
区域2:拟合函数为
Z(x, y) =(127.963 689 145 033-0.062 484 795 002 497 7·x +
1.830 925 780 497 71 ×10-5·x2-1.697 212 761 403 43 ×10-9·x3-
0.025 293 183 223 577 2·y +2.574 775 150 447 59 ×10-6·y2) ÷
(1 +2.200 663 662 954 41 ×10-5·x-0.000 432 268 802 680 673·y +
4.223 697 798 099 64 ×10-8·y2)
趋近无穷大点坐标为
X:2 925.763 113 015 66
Y:4 124.594 100 547 28
⑤Hg污染源的区域划分
区域1范围:2 000≤x≤3 500,1 500≤y≤4 000
区域2范围:13 000≤x≤15 000,1 000≤y≤4 000
区域3范围:8 000≤y≤10 500,8 000≤y≤10 500
模型建立及函数拟合求解
区域1:拟合函数为
Z(x, y) =(-172 747.816 848 209 +70.551 770 675 837 9·x-
0.010 472 270 397 803 2·x2+76.070 817 311 137 9·y-
0.033 179 955 477 673 7·y2+4.539 967 016 168 66 ×
10-6·y3) ÷ (1 +0.002 868 901 806 053 22·x-
1.001 829 747 056 67 ×10-6·x2-0.000 722 896 383 962 674·y)
趋近无穷大点坐标为
X:2 162.909 959 291 24
Y:3 483.814 509 596 28
区域2:拟合函数为
Z(x, y) =(-522 988.115 997 749 +87.809 007 010 529 3·x-
0.004 258 517 791 255 19·x2+5.110 495 200 826 63 ×10-8·x3-
5.429 853 327 446 88·y +0.000 711 443 375 078 052·y2) ÷(1 +
0.033 046 250 395 070 5·x-1.101 921 499 045 93 ×10-6·x2-
0.191 191 729 431 598·y +3.671 387 207 038 55 ×10-5·y2)
趋近无穷大点坐标为
X:13 527.800 632 712 1
Y:2 341.644 296 659 68
区域3:拟合函数为
Z(x, y) =(-0.071 928 753 636 026 3 +1.910 010 064 600 9·x-
0.126 105 313 146 735·x2+1.077 882 987 233 82·y +
0.353 490 693 027 901·y2) ÷ (1 +1.741 644 450 626 87·x +
0.471 030 474 457 907·x2+0.656 129 620 458 842·y-
1.321 138 847 037 23·y2)
趋近无穷大点坐标为
X:16 205.630 202 532 5
Y:9 677.805 300 495 63
⑥Ni污染源的区域划分
区域范围:2 500≤x≤5 000,4 000≤y≤6 800
模型建立及函数拟合求解
拟合函数为
Z(x, y) =(-78 856 317.806 893 3 +3 823.485 742 083 94·x +
25 370.915 646 470 2·y-2.339 218 229 432 55·y2) ÷
(1 +195.699 641 864 833·x-255.509 513 961 163·y +
0.024 964 403 097 942 1·y2)
趋近无穷大点为
X:3 336.182 954 594 6
Y:5 306.419 590 874 15
⑦Pb污染区域的划分
区域1范围:1 000≤x≤4 000,2 000≤x≤4 000
区域2范围:4 000≤x≤6 000,4 000≤y≤6 000
模型建立及函数拟合求解
区域1:拟合函数为
Z(x, y) =(787 730.412 563 236-75.891 310 290 085 8·x-
1 189.514 581 016 91·y +1.133 811 332 196 8·y2-
0.000 220 169 373 497 531·y3) ÷(1-29.705 676 490 983 8·x +
0.007 901 258 740 635 25·x2+22.071 903 687 372 4·y-
0.003 962 538 168 307 48·y2)
趋近无穷大点坐标为
X:1 870.008 658 404 1
Y:3 628.256 373 078 08
区域2:拟合函数为
Z(x, y) =(-23 688 957.524 955 2 +3 465.14 849 468 109·x-
0.317 693 082 905 813·x2+7 973.762 256 023 9·y-
1.444 719 591 357 69·y2+8.600 645 821 691 28 ×10-5·y3) ÷
(1-1.180 273 097 729 79·x +0.000 281 120 364 386 146·x2-
0.105 883 950 330 603·y)
趋近无穷大点坐标为
X:4 546.527 688 755 2
Y:4 210.936 239 927 96
⑧Zn污染区的划分
区域1范围:1 000≤x≤4 000,2 000≤y≤4 000
区域2范围:2 000≤x≤5 000,4 000≤y≤7 000
区域3范围:9 000≤x≤11 000,3 500≤y≤5 500
区域4范围:12 000≤x≤14 500,8 500≤y≤11 500
模型建立及函数你何求解
区域1:拟合函数为
Z(x, y) =(434.060 020 492 831-0.340 669 734 189 335·x +
3.503 563 020 985 31 ×10-5·x2+0.269 674 662 804 433·y-
5.610 922 008 207 34 ×10-5·y2) ÷ (1-
0.000 247 122 203 774 034·x-0.000 101 540 785 863 727·y)
近无穷大点坐标为
X:3 141.104 796 011 25
Y:2 203.678 636 334 5
区域2:拟合函数为
Z(x, y) =(-1.602 060 649 380 3 +98.135 851 385 502 8·x-
0.023 765 702 832 430 3·x2+1.978 327 693 939 86 ×10-6·x3-
22.016 167 462 876 8·y) ÷ (1 +0.076 834 232 942 538 2·x-
8.671 783 821 734 71 ×10-6·x2-0.026 271 376 744 550 58·y)
趋近无穷大点坐标为
X:2 000.022 060 940 13
Y:4 567.033 603 345 62
区域3:拟合函数为
Z(x, y) =(1 725 345.811 653 05 +178.771 893 278 626·x-
812.673 856 385 299·y) ÷ (1 +0.598 796 648 597 113·x +
2.008 140 772 316 43·y-0.000 768 461 573 824 596·y2)
趋近无穷大点坐标为
X:9 000.070 735 900 38
Y:4 259.814 635 043 75
区域4:拟合函数为
Z(x, y) =(-11 832 271.199 472 4-9 051.859 606 130 52·x +
0.846 495 618 887 497·y +1.477 220 470 659 85·y2) ÷
(1-0.319 181 524 853 977·x-0.134 164 443 370 786·x2-
8.722 048 097 053 57·y +0.276 863 493 443 413·y2)
趋近无穷大点坐标为
X:14 994.668 041 300 3
Y:10 454.721 824 377 8
(四)问题4
1.优缺点分析
(1)全面性:本文中的传播模型包含了众多影响传播的因素,由多种因素得到的数据逐次逼近得到的函数,有较高的拟合度。避免了单一套用大气模型等单一模型而造成的片面性。
(2)可用性:使用了LINGO 11.0,MATLAB,1stOpt,SPSS,Excel等软件对数据进行运算、整合、归纳,得出规范系统的数据。
(3)实际性:根据题目给出的条件,利用海拔的条件做出了模拟的山峰,使得山脚下凹陷处的重金属污染堆积问题得到了很好解释,切合实际。
(4)代表性:本模型具有比较广泛的代表性,以此确定范围即可得到相应的污染处的重金属浓度。
(5)直观性:本模型的实现运用了MATLAB做三维图像、散点图、等高线图等功能,可以从各个方位对拟合形成的曲面或散点进行分析。形象直观,易于理解与观测。
(6)由于条件中并没有相关的时间数据,造成了模型的瞬时性,不能达到很好的预测未来趋势的功能。
(7)选择的采样点是随机的,必然会导致误差。
(8)在可能有污染源的地方缺少集中的采样,使拟合出的函数不够精准
(9)土壤本身可能有污染差异,我们简单认为其无差异
2.模型的改进
加入模型1:高斯的实用性大气扩散模型
影响大气污染扩散的因素主要分为气象因素和地形因数两个方面[6]。而气象因素则包括风向、扩散等因素。我们结合本题的条件,是为一个城区,所以选取地面连续点源扩散模式作为基础来对大气扩散模型实现:
(1)需要条件
①相同采样点在不同风向等大气作用下的数据
②污染源的边际产量
③每个采样点的风速
(2)假设
①污染物浓度在y、z风向上分布为正态分布
②在全部的任何高度风速均匀稳定
③污染源源强是连续均匀稳定的
④扩散中污染物是守恒的(不考虑转化)
(3)符号说明
原点O为重金属污染源点
x为顺风向,y为横风向,z为垂直向时的坐标轴
C(x,y,z)为任意一个采样点的重金属浓度
q为污染源点的污染强度,即所有污染的排放量
u为风速
σy,σz为传播时的扩散系数
A(x)为重金属污染物在传播中的递减函数
a,b为未知常数
(4)模型的建立与求解
由于假设a正态分布假定,得到下风向任一点的浓度分布为下式:
c(x, y, z) = A(x) e- ay2e- bz2
同理由于假设a,得出关于y,z方差的表达式:
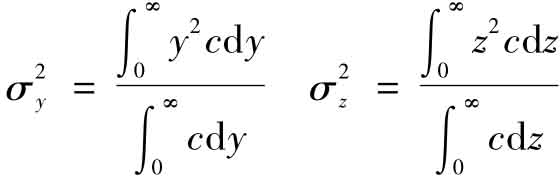
由于假定d,扩散中污染物是守恒的,则为始终等于污染源点的单位排出量:
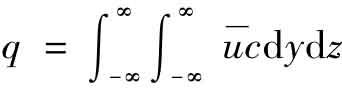
由以上等式进行积分等整合运算,可以解出:
得到高斯模式:
带回原式中c(x, y, z) = A(x) e- ay2e- bz2,得出如下的高斯实用大气扩散模型
为得到题目中市区地质环境的演变模式,我们可根据历年来不同情况下的数据进行总结归纳,统计分析,带入等式进行拟合逼近,得出该城区的大气高斯重金属污染程度模型。
加入模型2:土壤中金属扩散运移模型
(1)需要条件:土壤含水率,重金属分子在土壤中的扩散系数
(2)假设
①除了扩散作用,其余方式引起的重金属污染物运移很小以至于可以不考虑
②无不可控外力因素影响扩散
③重金属分子不会转化为离子形式
(3)符号说明
Q表示是溶质分子在土壤中的流通通量;
k表示溶质分子在溶液中的扩散系数;
c表示溶质的浓度;
x,y,表示空间坐标系中的x、y轴的方向;
θ表示土壤含水率;
t表示时间;
(4)模型的建立与求解
土壤重金属污染物在土壤中随着土壤水分的运移而运动,同时重金属污染物在运移的过程中还会受到土壤基质、重金属污染物本身的物理化学性质以及土壤中其他化学成分的影响。在此,我们不考虑后者,考虑随着水分移动而移动的情况。在其中,起到主要作用的是对流与扩散。对于对流我们将在之后的模型改进中研究,现在只研究扩散作用。
扩散是由溶质分子的热运动引起的,具有从高浓度处向低浓度处运移,以求达到浓度相等的趋势,其根本原因在于浓度的差异。在自由水溶液中,溶质的扩散遵循Fick第一定律,用数学表达式表示为:
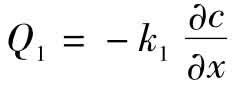
同样,在土壤溶液中,重金属污染物的扩散也遵循该定律,数学表达式为:
由于只有扩散,所以重金属在土壤中的运移总通量等于扩散通量,即
由质量守恒定律以及土壤水分运移的连续方程的含水量方程——θ方程,如下:
得到一维土壤重金属运移的连续方程为:
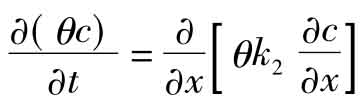
在二维情况下,容易得到其连续方程为:
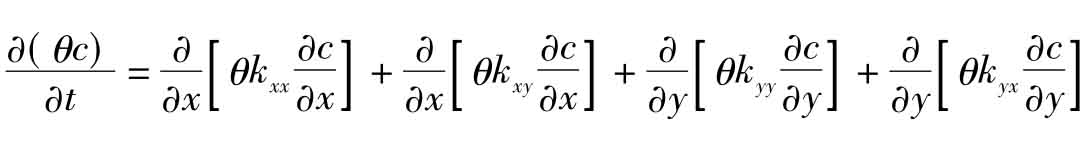
六、问题结论与分析
(一)问题结论的陈述
1.通过MATLAB作图得出8种重金属元素的空间分布,用两种标准都得到区域污染程度由高到低依次为:工业区、交通区、生活区、公园绿地区、山区。
2.经分析得到As,Cr,Cu,Hg,Ni,Pb,Zn污染可由工厂排污引起; Cd,Pb污染可由交通区车辆等因素引起; Cr,Cu,Hg,Ni,Pb,Zn污染可能由生活区垃圾集中处理引起。
3.确立两种传播特征:线形污染源的两旁扩散式传播和点形污染源的中心聚集,四周缓慢扩散式的传播。并得出15处污染源。
4.加入高斯的实用性大气扩散模型和土壤中金属扩散运移模型进一步完善城市地质环境演变研究模型。
(二)模型的检验与分析
1.误差分析
通过建立的模型,以原取样点坐标带入计算,得到计算值与实际测量值之间的误差,对误差进行相应的分析,验证模型的准确性。
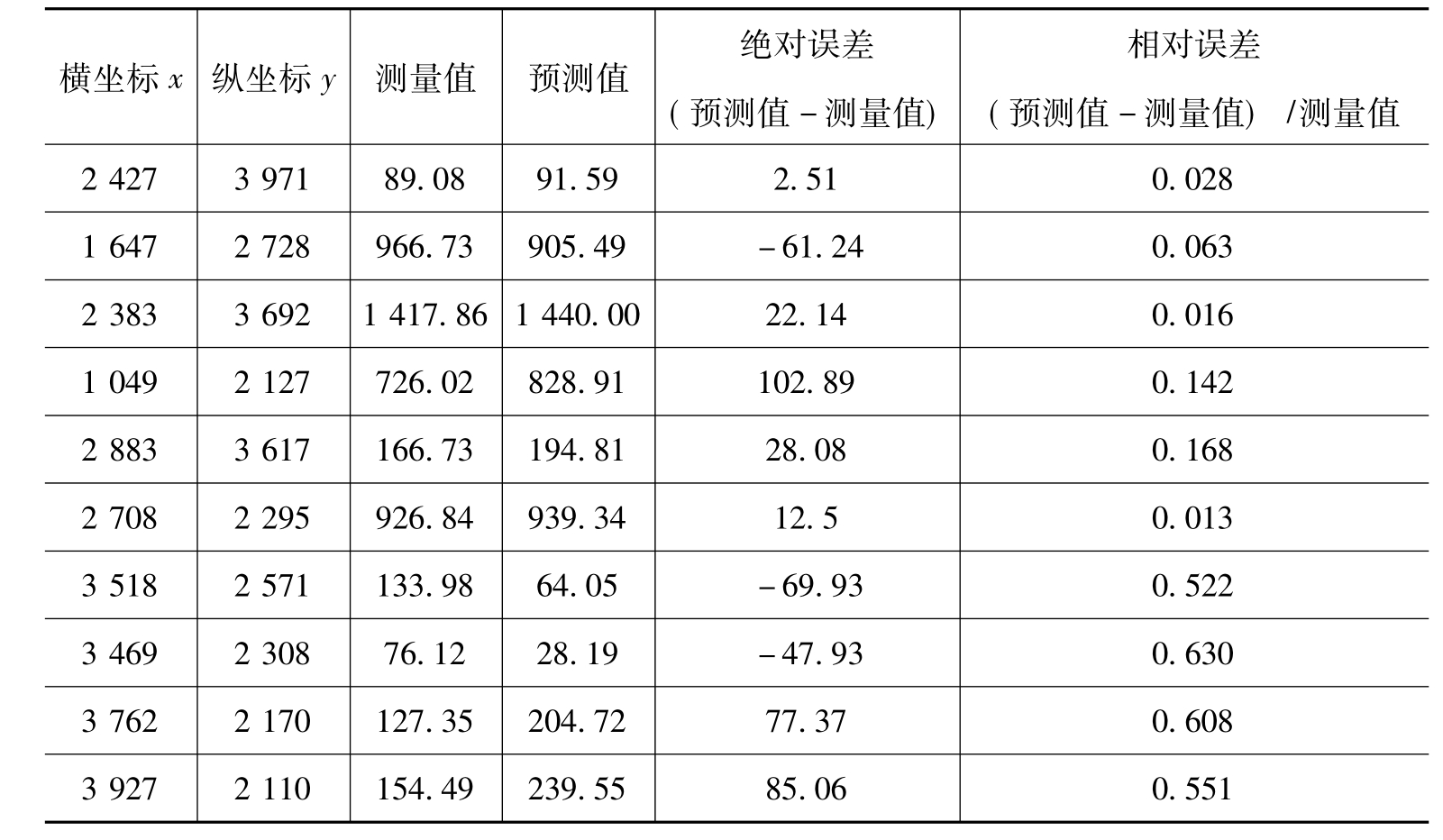
以上数据表明本模型与实际取样值吻合度很高,误差很小
2.模型数据的正态性检验
以As为例,将城区的所有采样点处的As浓度数值进行集中的分布处理,运用SPSS软件得到置信区间* =5%的情况下As的分布情况如下图一所示。图二中,Q- Q图上的点近似地在一条直线附近,该直线的斜率为标准差3.024 29,截距为均值5.676 5。并且获得了偏度和峰度的相应信息,即偏度:3.324,峰度:19.696。各采样点极好的回归于直线。由同样方法可以得到其他元素也近似服从标准正态分布,说明模型预测值与观测值在数量级方面接近较好。
图一
图二
3.模型的敏感性分析
我们的模型是以对每种元素污染点的分区讨论为基础的,模型计算的结果与所划分的区域有密不可分的联系。因此,我们让其横纵坐标范围适当的变化,通过研究模拟出的污染源位置的偏移程度来确定其敏感性。下面以Zn的第一分区为例:
由此表可以看出所划分区域横纵坐标的改变对所求出的污染源位置有较大扰动。实际上,每种元素的每种分区都有这种规律——所求污染源位置对所划分区域位置有较强的敏感程度。这是由于对具体的分区,我们拥有的采样点较少,平均7、8个,而改变分区大小后会减少或增加2、3个,这必然会改变所拟合出的函数,从而导致了污染源位置的改变。但是,两者所得到的污染源位置均与matlab模拟出的位置十分接近,这在某种程度上也验证模型的正确性。
(三)模型的评价与改进
在问题四中我们分析了土壤重金属扩散运移模型,现在我们再将对流作用加入模型,对模型进行改进,改进后的模型称为土壤重金属运移总通量模型。
此模型的需要条件、符号说明和大部分假设相同,仅将“除了扩散作用,其余方式引起的重金属污染物运移很小以至于可以不考虑”这一假设更改为“除了扩散以及对流作用,其余方式引起的重金属污染物运移很小以至于可以不考虑” 。
对流是指溶质随着土壤水分的运移过程而进行的运动过程。在单位时间内通过单位土壤横截面积的溶质质量称为溶质通量。溶质在土壤中的溶质通量与土壤水分通量和溶质的浓度有关,它们之间的关系可用数学表达式表示为:
Q3= CQw
重金属在土壤中的运移总通量是对流通量和扩散通量的总和,数学表达式为:
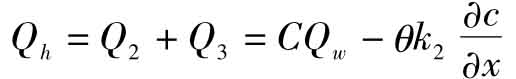
根据质量守恒原理,在所研究的土壤体积内,溶质的变化率应该等于流入和流出的溶质通量之差,再联系土壤水分的连续方程,可以推导出一维土壤溶质运移的连续方程为:
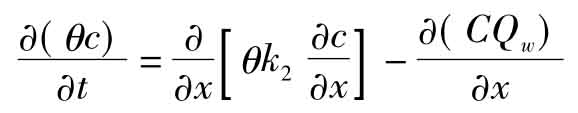
参考文献
[1]王琦,徐式蕴,赵睿涛,高军锋,常春藤.MATLAB基础应用与实例集萃.北京:人民邮电出版社,2007:59-83.
[2]谢兆鸿,范正森,王艮远.数学建模技术.北京:中国水利水电出版社,2003:227-232.
[3]徐争启,倪师军,张成江.潜在危害指数法评价中重金属毒性系数计算.环境科学与技术,2008,31 (2) :112-115.
[4]姜启源,谢金星,叶俊.数学模型.(第四版) ,北京:高等教育出版社,2011:325-356.
[5]刘锋.数学建模.南京:南京大学出版社,2005:120-153.
[6]解迎刚.基于GIS的大气污染源扩散模拟的实现及应用,http://www.epem.com/em/hydt/2010/0407/660.html,2011-09-12.
【注释】
[1]这里在计算时,将8种元素分别以数字编号,方便运算。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















