需求价格弹性的定义和计算

一、需求价格弹性的定义和计算

1.需求价格弹性的定义

需求价格弹性可以从几个角度定义，一是可以定义为价格变动对需求量产生的影响程度，二是可以定义为需求量对价格变动的反应程度，另一个操作性的定义是价格变化1%所引起的需求量变化的百分比。用E_d表示需求价格弹性系数，用P和ΔP分别表示变动前的价格和价格的变化量，用Q和ΔQ分别表示变动前的需求量和需求量的变化量，可得下列定义式：

这里，由于需求量和价格呈反方向变化，因此当价格提高时，需求量降低，价格降低时，需求量增加。所以，需求价格弹性系数为负值。不过，通常为了叙述方便，习惯上提到需求价格弹性系数时用绝对值，由此可以在需求价格弹性系数前加一个负号，将其转化为正值。

下面可举一个例子说明需求价格弹性的计算。

例如，某商店出售一种饮料，当价格为10元/瓶时，饮料的需求量^[1]为100瓶，当价格降低为5元/瓶时，饮料的需求量为300瓶。根据上述数据，可得：

P₁＝10，P₂＝5，ΔP＝P₂－P₁＝10－5＝－5

Q₁＝100，Q₂＝300，ΔQ＝Q₂－Q₁＝300－100＝200

则该种饮料的需求价格弹性为：

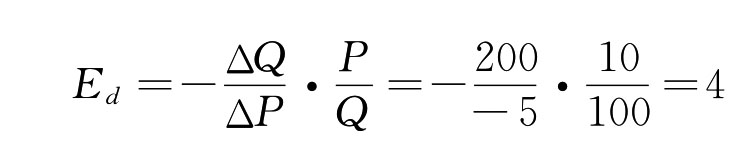
该结果表明，当该种饮料价格变化1%时，其需求量将变化4%。

2.弧弹性的计算

上述例子中，我们是以变化前的价格和需求量为基数计算的，如果将计算基数改为变化后的价格和需求量，就会得出一个完全不同的值，重新计算一下，可得：

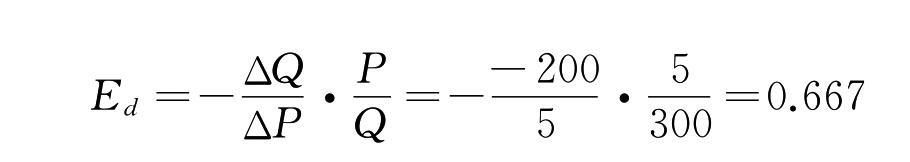
新的结果表明，当该饮料价格变化1%时，其需求量将变化0.667%。与前面的计算出现了较大的差异。这种差异产生的主要原因即在于计算的基础是不同的，此外，价格及需求量变化的幅度也较大。如图3.1所示，第一种计算是以A点的价格和需求量组合为基础的，而第二种计算则是以B点的价格和需求量组合为基础的。由于价格和需求量的变化在两种计算中都相同，但基础点上位于公式中分子和分母的价格和需求量值差异较大，从而造成最终计算出的弹性系数差异较大。

图3.1　弧弹性计算

如果图3.1中A和B点靠的足够近，上述两种计算得出的弹性值相差不会太大。当A和B点相距较远时，差异就会相当明显，为了修正这种缺陷，实践中通常采用价格和需求量变化前后的算术平均数来计算弹性系数。其基本计算公式是：

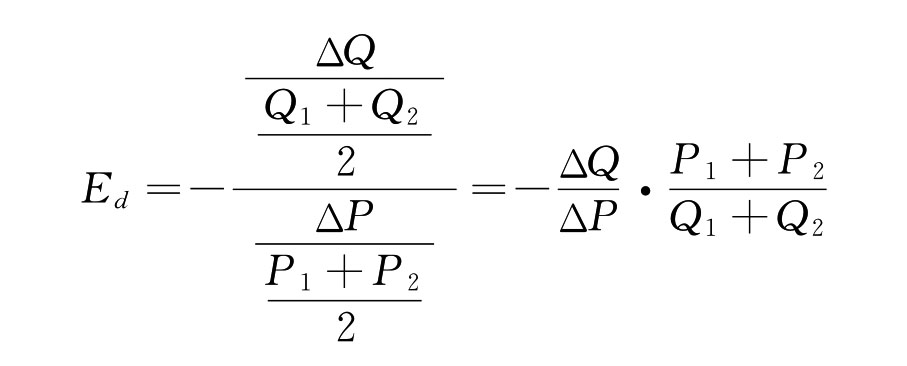
用上述公式来计算前面例子中的弹性系数可得：

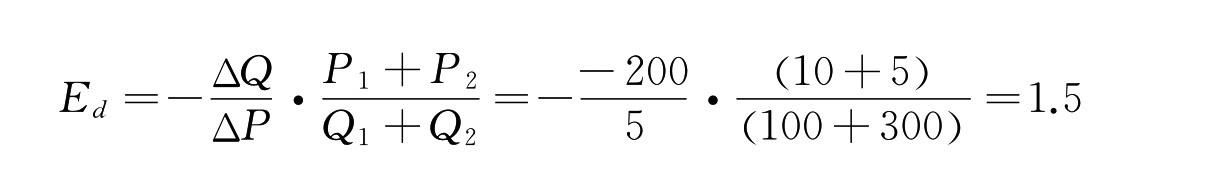
即当该饮料价格变化1%时，其需求量将变化1.5%，这一结果比较准确地度量了该饮料价格从10元到5元变化所引起的需求量变化程度。从图3.1也可以看出，上述公式度量了需求曲线上A点到B点间这一段曲线的弹性强度，因此上式称为弧弹性公式，表示需求曲线上某两点之间的平均弹性值。

3.点弹性的计算

当存在连续可导的需求函数时，我们还可以运用点弹性公式来计算需求价格弹性系数。这一公式可由微分的办法得到：

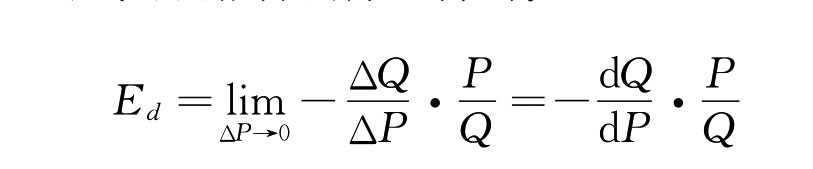
当需求函数(P＝P(Q))的形式^[2]给定时，上式中－d Q/d P就是需求曲线上在点(Q，P)的切线斜率的倒数，P/Q比值实际上确定了要考察的点的位置。如果我们使用的是线性的需求函数，则其斜率只有一个，这样只要给定一个点的位置，就可以通过与其斜率的负值相乘而得出该点的需求价格弹性值。例如，某商品的需求函数为Q_d＝30－2P，可得：

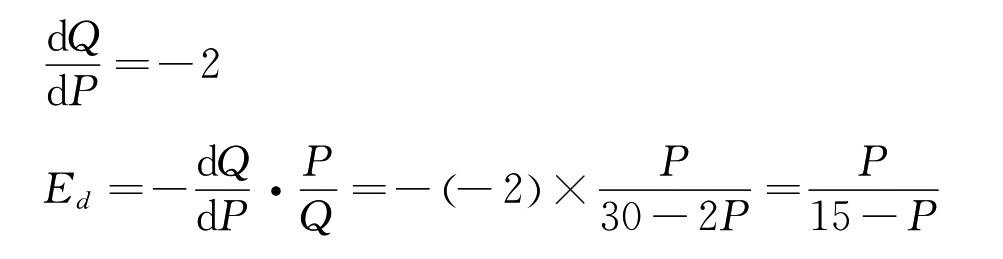
上述关系确定后，在每一个价格水平上(当一个价格给定，代入需求函数，相应的需求量也给定了)，都可以计算出相应的弹性系数值。例如，当P＝5时，E_d＝0.5；P＝10时，E_d＝2；P＝12时，E_d＝4，等等。