地方保护主义的危害

4.1.2　地方保护主义的危害

一、“飞去来器”——以害人出发以害己告终

说到地方保护主义的危害，有人曾把它比做为“飞去来器”。飞去来器是一种玩具，这种玩具你把它扔出去，它转一个圈儿，又会飞回来。地方保护主义者都想把利益留给自己，把危害扔给别人。结果这一危害最终会飞回来，从而伤害自己。

地方保护主义的危害，主要可以概括为:

第一，它颠倒了整体与局部之间的关系，不同程度地肢解了社会主义的统一市场，破坏了国民经济的整体统一性，影响了生产要素的的合理流动和配置。

第二，它瓦解了中央宏观调控的实力。地方保护主义的存在，表明国家汲取社会经济资源的能力下降。中央汲取财政的能力是国家能力的最主要体现，也是中央控制宏观经济能力的基础。中央财政能力下降，必然会削弱中央政府的权威，最终导致宏观调控的乏力。

第三，它保护落后，使企业无形中丧失了应有的竞争力，使得产业结构和产品结构难以优化，人为地导致产品的积压和企业经济效益的下降。

第四，它使得投资重复，消费失控。由于中央控制宏观经济的程度下降，应运而生的地方保护主义便各自为政、各自为战，结果既束缚了经济的规模化发展，又使社会经济秩序陷入了混乱。首先是投资急剧膨胀，投资重复现象严重。投资急剧膨胀往往拉动消费的恶性膨胀，从而形成消费失控局面，一时高消费、畸性消费成为时尚，奢侈之风愈演愈烈。

第五，从地方主义对区域经济发展的影响来看，地方保护主义不仅直接地起到了抑优扶劣的作用，而且限制了企业产品和原料的广阔市场，进一步加剧了市场的疲软，使得企业经济效益一挫再挫，直至将肥的拖瘦，瘦的拖死。

二、地方保护主义使得局部和整体利益均难以优化

地方保护主义的最大危害是，虽然从局部利益来看，当事人的利益都暂时地或相对达到了最大化，但是却同时损害了全局的利益，使得全局利益受挫，因而难以实现整体的最优化。有的人可能不相信这一点，说每一个局部单位的利益如果都达到最大化，那么全局的利益不是也就最大化吗?其实并非如此，因为全局的利益并不是局部利益的简单相加，这一点我们可以用博弈论的的原理加以证明⁽²⁾。

博弈论中有一个非常经典例子，即囚徒困境问题。问题是这样说的，警察抓住了两个罪犯，但缺乏足够的证据指证他们所犯的罪行。为了得到所需的口供，警察将这两个罪犯分别关押以防止他们串供或结成攻守同盟。同时根据犯罪的事实，如果罪犯中有一人供认犯罪，就能确认罪名成立。于是，他们两人被告知:如果两个人都拒不认罪，则因证据不足两人各被判刑1年;如果有1人坦白，则坦白者立即释放而另一人则被加重判刑8年(有道是，坦白从宽，抗拒从严);如果两人都坦白，则两人双双被判刑5年。如果分别用0、－1、－5和－8表示释放和判刑1年、5年、8年的得益，则可用一个特殊的矩阵将这个博弈表示出来，见图4－1。

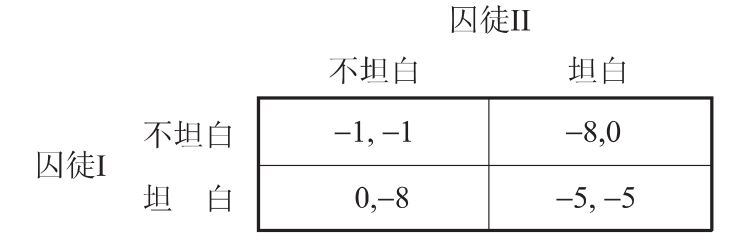
图4－1　囚徒的困境

图中的囚徒I和囚徒II分别代表博弈中的两个局中人，每人都有不坦白和坦白两种策略选择。但是双方最终的得益不仅取决于自己的策略选择，而且也取决于对方的选择。博弈总共有四中可能的结果，每一方的最好得益为0，最差得益是－8。双方的惟一目标都是实现自身的最大得益，那么他们各自应如何选择自己的策略呢?

由于在这里每一个局中人在选择策略时都无法知道对方会选择哪一种策略，所以，这里对策的基本方法就是先假定对方的某一种策略出现，然后选择自己的最好策略，最后再找到均衡策略(博弈论中称作纳什均衡)即可。比如，对于囚徒I来说，如果囚徒II选择不坦白，则囚徒I选择不坦白得益为－1，坦白得益为0，因此他无疑应选择坦白较好;再假设如果囚徒II选择坦白，则囚徒I不坦白得益为－8，坦白得益为－5，在这种情况下显然他也应选择坦白较好。也就是说，无论囚徒II选择哪种策略，囚徒I都只有一种选择即坦白，因为只有这样，他才能获得最好得益。同样道理，囚徒II的惟一选择也只有坦白。所以该博弈的均衡策略就是(坦白，坦白)，结果两囚徒双双被判刑5年。

很显然，无论是对于两个囚徒总体来说，还是对于他们每一个人而言，最好的结果都不是同时坦白得到(－5，－5)的得益，而是都不坦白得到(－1，－1)的得益。然而由于两囚徒在决策时是背靠背进行的，在信息不足的情况下两人都要以自身的最大利益为目标，结果是两者谁都无法实现最大利益，只能舍最大利益而求其次。当然，两个人完全可以通过订立攻守同盟的方法，约定选择(不坦白，不坦白)策略，以便获得(－1，－1)的得益。然而，这一策略并不是纳什均衡，因而对于决策双方来说没有任何约束力。因为，对于每一个囚犯而言，都存在着当对方选择“不坦白”而自己选择坦白被无罪释放的诱惑。这种现象在现实生活中是普遍存在的，在市场竞争、资源开发和环境问题中都屡见不鲜。这一例子充分说明了每一个体都从自身利益最大化出发，却并未得到全局最大化的结论。

下面我们再来看一个有关经济问题的例子。这就是博弈论中有关产量决策的古尔诺模型，是由法国经济学家古尔诺(A.A.Cournot，1801－1877，也译为库诺)于1838年提出的。

该模型假定，市场上有n个厂商销售完全相同的产品，由于市场容量有限，因此在一定的价格水平上只能有有限数量的产品售出，或者说能够将产品全部销出的“市场出清价格”是投放到该市场上的该产品总量的函数。商品的总量就是这n个厂商的产量总和。另假定这n个厂商的产量决策是相互独立且不受任何限制的，并且总是在同时决定各自的产量(在这里，同时决策的含义主要是说每个厂商在决定自己的产量时根本无法知道其他厂商的决定)，问这n个厂商应如何进行产量决策?

己的产量决策q_i，也还通过价格受制于其他厂商的产量决策，因此，他在决策时必须考虑其他厂商的决策方式和对自己决策的可能影响。

为了说明方便起见，现假定市场上只有两家厂商，各自的产量分别为q₁和q₂，则全

部厂商的总商品量为Q=q₁+q₂。再设市场出清价格P是Q的函数，即P=f(Q)=8－Q，假定两厂商的单位成本相等，即有c₁=c₂=2。于是，得到两个厂商的利润函数分别为: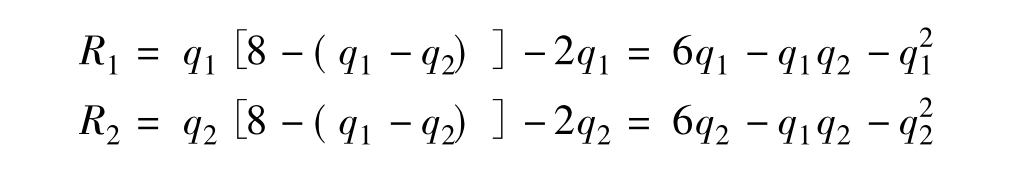

在本博弈中，寻找均衡策略的充分且必要条件是求出q₁和q₂的最大值，即: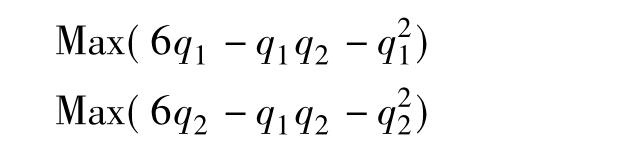

根据数学分析原理，只要解方程组: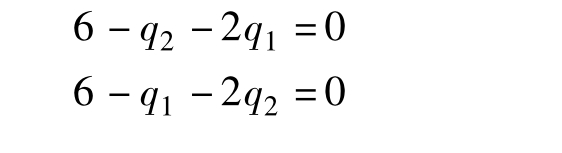

解之，得到q₁=q₂=2。于是，双方的得益即利润均为:2×(8－4)－2×2=4。市场总商品量为2+2=4，两厂商的利润总和为:4+4=8。

其实，市场的总得益应该是方程:R=Qf(Q)－cQ=Q(8－Q)－2Q=6Q－Q²最大值，其最大值总产量为Q=3，总利润为:R=9。比原来各自独立决策时的总产量少1个单位，但获得的总利润却多1个单位。即从总体最优的目标出发，既节约了资源，又取得了更优的效益;而各自都要达到最优，则既浪费资源，效益还更差。

古尔诺模型只不过是囚徒困境问题的一个变种，该模型有力地说明了个体利益最大化未必能得到总体利益的最大化。这一模型在现实中的最好例子就是石油输出国组织规定的生产限额和限额的不断被突破。石油输出国组织成员都深知，如果他们都各自为政自定产量，结果肯定是油价下跌，利润受损，因此必须共同磋商制定产量限额以维持油价(在古尔诺模型中，价格正是产量的减函数)。但同时每一个成员国也都知道，如果其他成员国都遵守限额，只有自己超产，他就会按照规定价格或市场价格获得更多的利润。于是，私下里便纷纷偷偷超产，结果限产计划破产，油价严重下跌，直至各国都得到最不能令人满意的纳什均衡为止。

我们不妨考察一下历史:1960年，由5个产油国发起成立欧佩克(OPEC，石油输出国组织Organization of Petroleum Export Countries)。1973年，成员国扩大到13个。当时各国还少有产量欺骗行为。1973年，阿－以战争爆发，为了报复以色列和西方国家，OPEC突然大幅度削减石油出口，致使世界原油价格由$2.91/桶暴涨到1974年$10.77/桶。这一意外事件让OPEC看到了组建卡特尔的诱人前景。1978年伊朗发生革命，其石油生产一度陷于瘫痪，继而两伊战争爆发，许多石油设施遭到破坏，世界石油价格进一步涨到80年代初的$40/桶。但是，高额的利润导致各个国家的产量欺骗行为(实际产量大于限产计划)，即各国不再遵守产量协定，擅自提高产量以获取更大的市场和更多的利润，从而导致石油价格下跌——当然，价格下跌也与世界其他地区如墨西哥油田、阿拉斯加油田、北海油田等石油供给增加有关。1982年世界石油价格为$32/桶，1984年为$27/桶，1987年为$18/桶，以后基本上在$15－18/桶之间波动。

类似的另一个例子是关于资源利用问题，该例子也成为公共草场问题。是说某个村庄有多个农户以牧羊为生，该村有一片大家都可以自由放牧的公共草地。由于这一片草地的面积有限，因此草地的数量只能让一定数量的羊只吃饱。如果在草地上放牧的羊只的数量超过了这个限度，每只羊都无法吃饱，从而羊的产出即毛皮肉的总价值就会减少，甚至羊只只能免强存活或饿死。假设各个农户在确定自己养羊的数量时不知道其他农户的养羊数目，即各个农户养羊数的决策是同时作出的，再假定所有农户都清楚这片公共草地最多能够养多少只羊以及各个规模水平条件下每只羊的产出，这就构成了一个多个农户之间关于养羊数量的博弈问题。

为了讨论方便，我们假定这个村只有三户牧民，各自的养羊数分别为q₁、q₂、q₃，则每只羊的产出应为养羊总数的减函数，假定为V=f(Q)=100－Q=100－(q₁+q₂+ q₃)，成本假定都是c=4，同时我们假定养羊的数量是连续可分的，于是三个农户的得益函数分别为: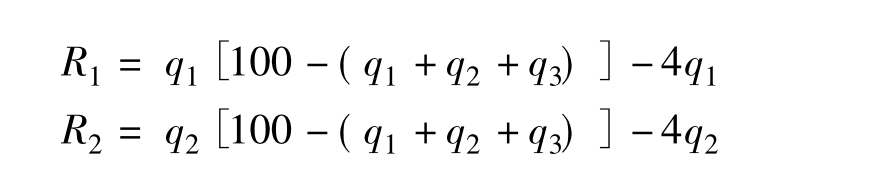

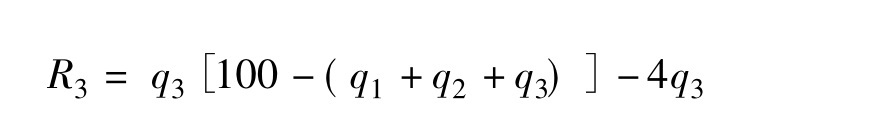
分别求得益对于养羊数的一阶微分，并让其为零，得到: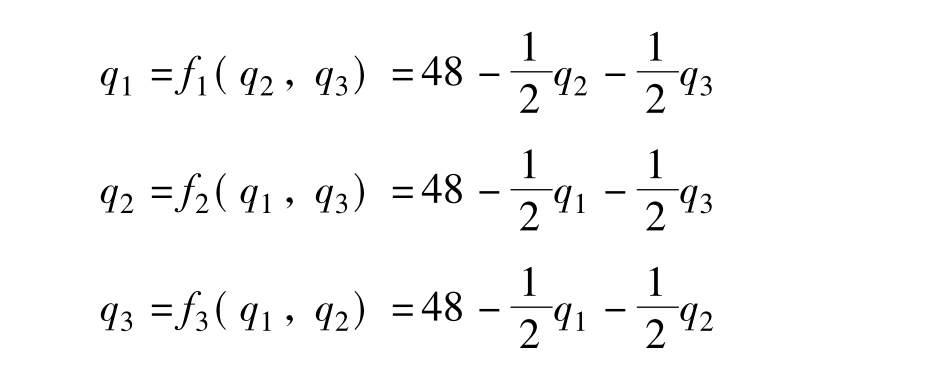

博弈论中将这三个函数称作其中一个局中人对另外两个局中人决策的反应函数。三个函数的交点(q₁，q₂，q₃)就是博弈的纳什均衡。解此联立方程组，可得到q₁=q₂= q₃=24，分别代入得益函数可得到R₁=R₂=R₃=576。这时的总得益为576×3=1728单位。实际上，如果从总体角度考察，总得益应该是: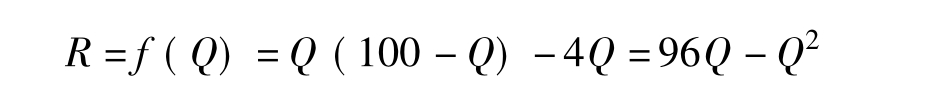

求其最大值得到R(48)=2304单位，比三个农户在各自独立决策时的得益要大的多。也就是说，从全局利益来看，各户的最佳养羊数应该是48/3=16只，而不是24只。

这个例子又一次说明了个体利益最大化未必会得到总体利益最大化。之所以会出现这样的悲剧，原因就在于，每一个可以利用公共资源的人都相当于面临着一种囚徒困境:当总体上有加大利用资源可能时，自己加大利用而其他人不加大利用则自己得益;而自己加大利用别人也加大利用则自己不至于吃亏，最终是所有的人都加大利用资源，直至达到纳什均衡为止。在古尔诺模型中，每一个局中人所面临的也是这种情况，即自己增加产量别人不增加产量自己得益，而自己增加产量别人也增加产量则自己不至于吃亏。这就正像囚徒困境中的每一个囚徒一样，对方选择坦白他选择坦白对自己是有利的，对方选择不坦白他选择坦白对自己也是有利的。这种现象，有人经常把它概括为“搭便车”现象，即对于搭便车的人来说，不管别人的选择是搭还是不搭，他选择搭对自己总是有利的。

博弈论的分析表明，地方保护主义现象是效率的大敌。因此要提高区域经济效率，就必须遏制地方保护主义现象的发展和蔓延，就必须树立全国一盘棋的思想，个体利益必须服从全局利益。我们经常强调，最优化问题是一项系统工程，也就是这个意思。