经常项目的理论模型

一、经常项目的理论模型

本章采用无限期小国开放经济模型作为理论分析的基本框架。假定该经济中存在单一的无限期生存的代理人，并且其效用函数是可加的，瞬时效用函数为非二次型的，满足u'＞0，u″＜0以及u″＞0。第t期代理人的收入y_t是随机变量，并且假定其服从随机游走过程，即y_t=y_t－1+ε_t，其中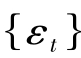是独立同分布的随机变量，且服从均值为0、方差为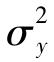的正态分布。代理人能够以常利率r＞0借入或借出，有b_t+1=(1+r)b_t+y_t－c_t，其中b_t是代理人在第t期期初的净资产，c_t是第t期的消费。代理人最优化问题为:

s.t.b_t+1=(1+r)b_t+y_t－c_t　　　(2)

其中，β为主观贴现因子，0＜β＜1，而b₀为给定。

对于代理人最优化问题，其值函数记为v(b_s)=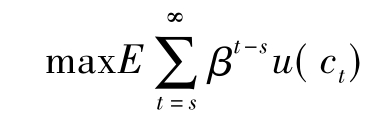，则与最优化问题(1)相对应的贝尔曼方程为:

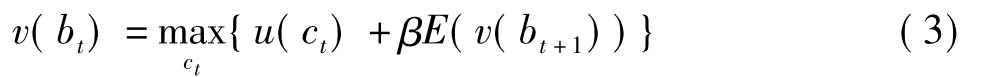
将(2)式带入(3)式，得到:

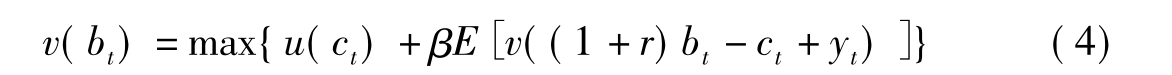
假设最优消费决策为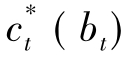，则(4)式的一阶条件为:

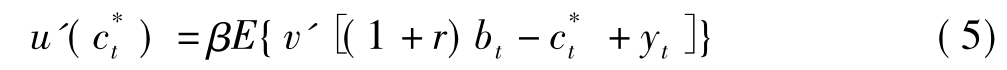
将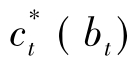代入(4)式，两边对b_t求导，并且应用包络定理，得到:

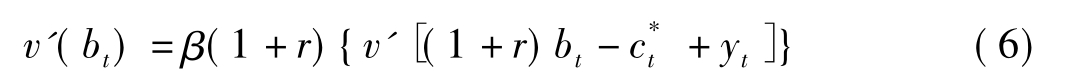
由(5)式和(6)式我们可以得到欧拉方程:

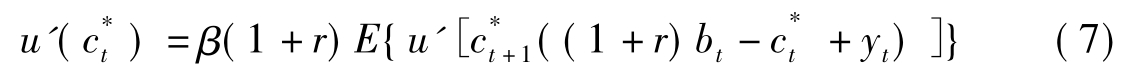
假定代理人的效用函数为绝对风险规避(CARA)型效用函数:

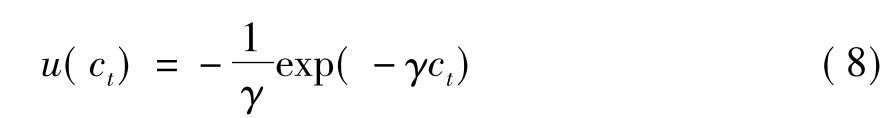
其中γ为常绝对风险回避系数。对于CARA型效用函数，从欧拉方程(7)式我们可以验证最优消费函数是净资产的线性函数，则可将其函数表达式表示为:

将(8)式和(9)式代入(7)式，并将y_t用随机游走过程表达式替代，可以得到:

exp［－γ(α₀+α₁b_t)］=β(1+r)Eexp{－γ［α₀(1－α₁)+α₁((1+r－α₁)b_t+y_t－1+ε_t)］}　　　　　　　　(10)

对于(10)式b_t取任意值等式关系均成立，那么－γα₁b_t=－γα₁(1+r－α₁)b_t必须成立，因此我们可以得到α₁=0或者α₁= r。舍去为0的值，我们将α₁=r代入(10)式，得到:

exp(－γα₀r)=β(1+r)Eexp{－γ［r(y_t－1+ε_t)］}(11)

将(11)式两边取自然对数并整理得到:

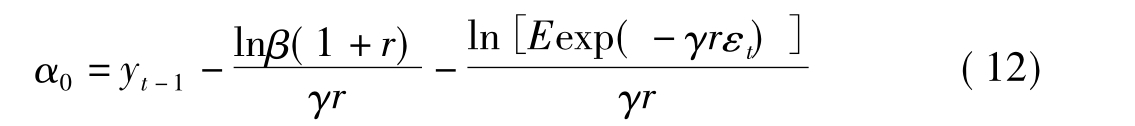
又由于假定{ε_t}是独立同分布的随机变量，且服从均值为0，方差为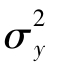的正态分布，我们可以得到:

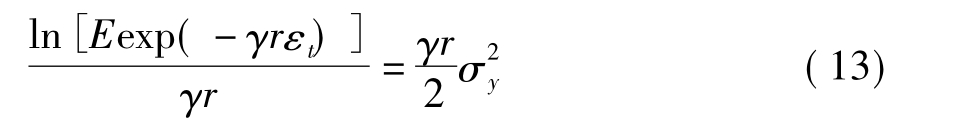
将(13)式带入(12)式，得到:

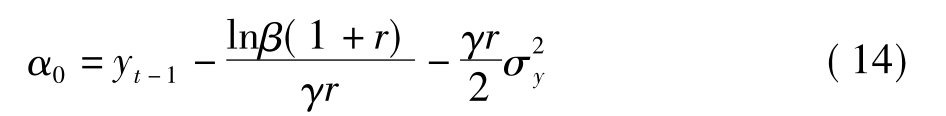
由(9)式和(14)式，得到:

设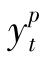是第t期的持久收入，则有:

将(17)式代入(15)式，得到:

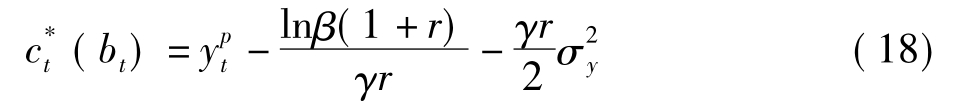
用ca_t表示第t期末代理人的对外资产积累，由于经常项目衡量的是对外净资产变化，那么ca_t也就是经常项目差额，并且有如下关系式:

ca_t=b_t+1－b_t　　　(19)

将(2)式和(17)式代入(19)式，并且整理得到:

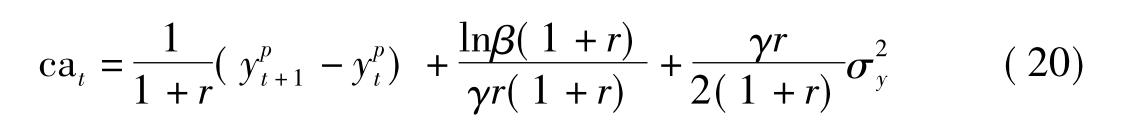
从(20)式我们得到在无限期小国开放经济模型下经常项目差额表达式，它是经过持久性收入的差分项经过两个其他影响因素作用得到的:一个是主观贴现因素，另一个是体现预防性储蓄的风险升水。