寡占理论的分析工具

第一节　寡占理论的分析工具

作为20世纪80年代引入的一种新方法，博弈论在产业组织理论中得到了广泛应用。博弈论本身的特点决定了博弈论思想成为了寡占理论的重要分析工具。博弈论是研究多人决策问题的理论，这类问题在经济学研究中经常会遇到。例如，我们已经比较熟悉的寡头市场就是典型的多人决策问题，其中每一个厂商都必须考虑其他厂商的行为。也就是说，如果其他厂商的产量较大，导致市场比较“拥挤”，卖出商品更加困难或者价格较低，所考察厂商的利润就会下降。反过来，若其他厂商的产量较低，所考察厂商的利润和最佳产量就会较高。可见，厂商之间的决策存在着明显的相互依赖关系。

一、博弈的内涵和要素

博弈是指一些个人、队组或者其他组织，面对一定的环境条件，在一定的规则下，同时或者先后，一次或者多次，从各自允许选择的行为或者策略中进行选择并加以实施，各自取得相应结果的过程。

（一）博弈的要素

任何一个博弈都需要包括下面四个要素:

1.参与人（Players）

参与人就是一个博弈中进行独立决策、独立承担结果的个人或者组织。一般来说，博弈的参与人可以是一个人、一个组织、一个国家等。在博弈的规则确定以后，各个参与人都是平等的，都必须按照规则行动。

2.各个参与人各自选择的行为集合（Action Sets）

各个参与人各自选择的行为集合，即每个参与人在进行决策时，可以选择的方法、做法或者策略。如果博弈不同，参与人可选择的行为和策略也会不同，即使在同一个博弈中，不同的参与人的行为内容和数量通常也是不同的，可以是一个，也可以是多个，还可以是无限个。

3.参与人的收益（Payoffs）

对于博弈各方，每一组可能的决策选择都会有一个结果，该结果表明了各个参与人的得失。

4.博弈的规则（Rules）

博弈的规则是对一项具体的博弈做出的具体规定。它包含对参与人行动顺序的规定、参与人行动时拥有信息多少的规定、有什么样的行动可供选择、选择之后的不同结果等。

下面用一个简单的例子进行说明。

假设有一对情侣，各自在不同的地点工作。下班后，双方由于客观原因无法联系上，但是他们希望能够在一起共进晚餐。他们常去吃饭的地点有两处:一是利顺德，二是喜来登。如果他们能够碰在一起，双方共进晚餐，感到非常幸福；如果碰不到一起，各自将在闷闷不乐中进餐。^[1][2]那么这个例子中的各项要素如下:①参与人。情侣1和情侣2。②行为集合。这里有四种可能情况，即（情侣1去利顺德，情侣2去利顺德）、（情侣1去利顺德，情侣2去喜来登）、（情侣1去喜来登，情侣2去喜来登）和（情侣1去喜来登，情侣2去利顺德）。③参与人的收益。要么是共进晚餐的幸福喜悦，要么是各自吃饭的闷闷不乐。④博弈规则。参与人是分开的，并且不能沟通信息。各自独立作出何处就餐的决定。

确定了上述四个方面的要素，就相当于确定了一个博弈。博弈论就是系统地研究可以用上述方法定义的各种博弈问题，寻求在各方具有充分或者有限理性、能力的条件下，合理的策略选择和合理选择策略时博弈的结果，并分析这些结果的经济意义、效率意义和方法。 ^[3]

（二）博弈的划分

一般来说，按照参与人行动的先后顺序，可以分为静态博弈和动态博弈。静态博弈是指参与人同时选择行动或非同时行动，但后行动者并不知道前行动者采取了什么具体行动的情况；动态博弈是指参与人行动有先后顺序，且后行动者能够观察先行动者选择的行动的情况。按照参与人对其他参与人的特征、战略空间及支付函数的知识，又可以分为完全信息博弈和不完全信息博弈。完全信息博弈是指每一个参与人对所有其他参与人（对手）的特征、战略空间及支付函数有准确的知识，否则为不完全信息。如果把这两种情况进行组合，则博弈的类型分为如表2-1所示的四种类型。

二、标准式博弈与纳什均衡

在博弈的标准式表述中，每一个参与人同时选择一个战略，所有参与人选择战略的组合决定了每个参与人的收益。我们这里借用经典的囚徒困境的例子来说明博弈标准式。^[4]

表2-1　博弈的类型

（一）囚徒困境

两个犯罪嫌疑人被捕并受到指控，但除非至少一个人承认犯罪，警方并没有充足的证据将其判刑。警方把他们关入不同的牢房，并对他们说明不同的行为带来的后果。如果两个人都不坦白，将都被判为轻度犯罪，入狱1个月；如果双方都坦白招认，都将判入狱6个月；如果一人招认而另一人不招认，招认的一方将马上获释，而另一人将判入狱9个月。

囚徒面临的问题可用表2-2的双变量矩阵进行表述。负的数字表示判刑的月数，也是两个参与人的收益，0代表获释。

表2-2　囚徒的困境

在这里，每个参与人（囚徒）都有两个战略选择:招认和沉默，在两个人的选择确定以后，就会形成四个战略组合，矩阵中的数据分别表示囚徒1和囚徒2的收益（囚徒1的收益在前，囚徒2的收益在后）。

在表2-2中，如果一个参与人选择了招认，那么另一个参与人也会选择招认，从而被判刑6个月，他不会选择沉默而判刑9个月。同样，如果一个参与人选择沉默，另一个参与人还会选择招认而获释，不会选择沉默被判刑1个月。那么，对于任意一个参与人来说，招认都是一个最优选择，沉默成为一个劣战略。因为对于囚徒j（j＝1，2）的每一个战略选择，囚徒i（i＝2，1）选择沉默的收益要小于选择招认的收益。

一般来说，在一个标准式的博弈中，设参与人i的可行战略为S₁和S₂，如果对于其他参与人的每一个战略组合，参与人i选择S₁的收益都小于选择S₂的收益，我们称S₁相对于S₂来说是严格的劣战略。

由于任何一个理性的参与人都不会选择严格劣战略，所以在囚徒困境中，两个人都会理性地选择招认，这样（招认，招认）就成为最终的结果，尽管给双方带来的收益都比（沉默，沉默）要低。

（二）重复剔除的严格劣战略

考虑表2-3的一个抽象的例子，参与人1的可选战略为S₁=｛上，下｝，参与人2有三个可选战略S₂=｛左，中，右｝。经过观察下面矩阵可以发现，参与人1目前不存在严格劣战略，而对于参与人2来说却是存在的，即参与人2选择“右”严格劣于选择“中”。

表2-3　重复剔除的例子

如果参与人1知道参与人2是理性的，他就可以把右从参与人2的战略空间中剔除，剔除后的博弈为如表2-3所示。这时候参与人2就没有严格的劣战略，但参与人1却出现了严格的劣战略，即下是上的严格劣战略。如果参与人1是理性的，他就不会选择下。如果参与人2知道参与人1是理性的，并且参与人2知道参与人1知道参与人2是理性的，也就是参与人2知道原博弈将简化为表2-4的形式，那么参与人2将会把下从参与人1的战略空间中剔除，所剩的结果如表2-5所示。这时参与人1只有一个战略选择，参与人2的最优选择显然是中，所以最后的博弈结果就是（上，中）。

表2-4　第一次剔除后的矩阵

表2-5　第二次剔除后的矩阵

上面的这个过程就称为“重复剔除严格劣战略”，这个剔除过程是建立在理性参与人不会选择严格劣战略的基础上的。但这仍有两个缺陷:一是参与人之间必须相互了解，也就是说“参与者是理性的”是共同知识。二是这种方法对结果的预测有时候是不精确的，特别是有的博弈战略矩阵并没有严格劣战略可供剔除。下面我们给出“纳什均衡”的概念，这个概念比上述方法应用广泛。

（三）纳什均衡

如图2-1所示的博弈矩阵，可见该矩阵不能采取上述的重复剔除的办法寻找均衡，我们按照纳什均衡的定义进行寻找，比如对于（R₁，C₁）来说，如果在参与人A选择了R₁的前提下，参与人B的最优选择是C₁，符合纳什均衡的一个方面；但是如果在参与人B选择C₁的前提下，参与人A的最优选择却是R₂。显然组合（R₁，C₁）不符合双方在给定的策略下不愿意调整自己策略的条件，所以该组合不是纳什均衡。依次，我们对其他的8个组合分别进行相同的分析，发现（R₃，C₃）符合纳什均衡的条件。因为在给定参与人A选择R₃的条件下，参与人B的最优选择是C₃，在给定参与人B选择C₃的条件下，参与人A的最优选择是R₃。可见在组合（R₃，C₃）条件下，二者都不愿意再调整自己的策略，所以是纳什均衡。

图2-1　寻找纳什均衡

对于表2-3中重复剔除的例子来说，最终结果（上，中）也是纳什均衡。再看下面图2-2的一个例子。如果使用重复剔除的方法，我们可以发现不同的提出方法有不同的结果。如果按照R₃、C₃、C₂、R₂的剔除顺序，最终的战略组合是（R₁，C₁）。如果按照C₂、R₂、C₁、R₃的剔除顺序，最终的战略组合是（R₁，C₃）。可见这两个组合都符合纳什均衡的条件。

由此，我们可以得出纳什均衡和重复剔除严格劣战略均衡之间的关系。一般来说，如果重复剔除严格劣战略，最终的结果是唯一的，即纳什均衡，但是如果结果并不唯一，那么这多个结果中有的可能是纳什均衡，有的可能不是纳什均衡。反过来说，如果一个组合是纳什均衡，那么它一定不会在重复剔除的过程中被剔除掉。

图2-2　不同剔除方法不同结果的例子

三、扩展式博弈

上述用标准式表述囚徒困境的例子和纳什均衡，可以说是完全信息静态博弈的分析。这里我们引入博弈的扩展式表示方法，这种方法更适宜于描述动态博弈的例子。^[6]

（一）扩展式的定义

一个博弈的扩展式包括:①博弈中的参与人；②每一参与人在何时行动；③轮到某一参与人行动时，可供他选择的行动以及他所了解的信息；④参与人可能选择的每一行动组合相对应的各个参与人的收益。

扩展式博弈通常使用博弈树来表示，下面我们用一个完全且完美动态博弈的例子进行说明。完全且完美信息的主要特点是:①行动是顺序发生的；②下一步行动选择之前，所有以前的行动都可以被观察到；③每一可能的行动组合下参与者的收益都是共同知识。

下面考虑一个两步博弈。第一步，参与人1选择支付1000元给参与人2或者一分不给；第二步，参与人2先观察参与人1的选择，然后决定是否引爆一颗手雷把两人一块炸死。假设参与人2威胁参与人1，如果他不付1000元就引爆手雷，如果参与人1相信这一威胁，他的最优反应就是支付1000元；但参与人1却不会对这一威胁信以为真，因为他不可置信:如果给参与人2一个机会，让他把威胁付诸实施，参与人2也不会选择实施，这样参与人1就会一分不付。

这个两步博弈有四个可能结果，即（给钱，不炸）、（给钱，炸）、（不给钱，不炸）和（不给钱，炸）四种类型。其中组合中前一个是取自参与人1的行为集合｛给钱，不给钱}，后一个取自参与人2的行为集合｛炸，不炸｝。假定与这四种类型结果对应的两个人的收益组合为（-1000，1000）、（-3000，-2000）、（0，0）和（-2000，-2000）。这样我们可以把这个过程描述为一个博弈树的形式（见图2-3）。

图2-3　博弈的扩展式表述

我们通过逆向归纳方法进行分析，首先从第二阶段分析，由于参与人1在第二阶段已经选择了自己的行动，参与人2就要在参与人1行动的基础上选择自己的最优行动。可见，不管参与人1给钱还是不给钱，参与人2的最优选择都是不炸。如果参与人1知道参与人2的最优选择就是不炸，那么参与人2的威胁就是不可信的，参与人1就会选择不给钱。

（二）逆向归纳法

根据上面分析的手雷博弈，我们把博弈进行一般化。

（1）参与者1从可行集A₁中选择一个行动a₁；

（2）参与者2观察到a₁之后从可行集A₂中选择一个行动a₂；

（3）两人的收益分别为u₁（a₁，a₂）和u₂（a₁，a₂）。

我们可以通过逆向归纳法求解此类博弈问题，方法如下:当在博弈的第二阶段参与者2行动时，由于其前参与者1已选择行动a₁，他面临的决策问题可用下式表示: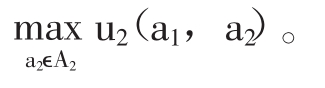

逆向归纳解不含有不可置信的威胁:参与者1预测参与者2将对参与者1可能选择的任何行动a₁作出最优反应，选择行动R₂（a₁）。

这一预测排除了参与者2不可置信的威胁，即参与者2将在第二阶段到来时作出不符合自身利益的反应。也就是说，参与者2的所有威胁信息都是不可信的，在第二阶段来临之时他会放弃不可信的威胁，转而实施有利于自己利益的行为策略。

四、重复博弈

在前面用扩展式表述的完全信息动态博弈中，前一阶段的选择决定了后面行动的结构，所以后一个阶段的行动结构往往不同于前面的行动。这样的动态博弈通常称为“序贯博弈”。另一种类型的博弈是重复博弈，是指同样结构的博弈重复多次的博弈。参与人之间长期互动的性质告诉我们，博弈的不同阶段是相互依赖的，这就使得理性参与人的决策不仅受其过去经历的影响，其决策还要受未来可能的影响。我们生活中许多有趣的行为模式，如奖励、惩罚、传送与泄露信息等都可以看做是多阶段动态博弈。动态博弈中最重要的是重复博弈，即每个阶段的博弈结构是相同的。

一般来说，重复博弈具有以下基本特征:^[7]①阶段博弈之间没有物质上的联系，也就说，前一阶段的博弈不改变后一阶段博弈的结构。②所有参与人都观测到博弈过去的历史。③参与人的总支付是所有阶段博弈支付的贴现值之和或加权平均。

正是由于参与人过去的历史都是可以观测的，一个参与人在一个阶段的选择依赖于其他参与人过去的历史，所以参与人在重复博弈中的战略空间远远大于并复杂于每一个阶段的战略空间。

我们这里讨论一个重复两次的囚徒困境模型。^[8]可以理解为警察给两个囚徒两次交代的机会，两个囚徒的最后收益是两个阶段博弈中各自收益之和。在这个博弈构成的两次重复博弈中，两博弈方先进行第一次博弈，双方看到第一次博弈的结果以后再进行第二次博弈。

根据逆向归纳法，先分析第二阶段两博弈方的选择。由于前一阶段的结果已经成为事实，此后也不再有后续阶段，因此实现自身当前的最大利益是两博弈方在该阶段决策中的唯一选择。所以我们不难得出结论，不管前一次博弈的结果如何，第二阶段的唯一结果就是原博弈唯一的纳什均衡（招认，招认），双方收益为（-6，-6）。

我们再回到第一阶段。理性的博弈方在第一阶段就对后一阶段的结局非常清楚，知道第二阶段的结果必然是（招认，招认）。因此，不管第一阶段的博弈结果是什么，双方的最终收益都将是第一阶段收益基础上各加-6。那么，从第一阶段来看，博弈就便成了如表2-6所示的矩阵。

表2-6　两阶段重复博弈中囚徒困境的第一阶段变形

表2-6中的矩阵不过是原表2-2矩阵的所有收益加上-6得到的，不会改变博弈的均衡，所以仍然有唯一的纳什均衡解（招认，招认），收益组合为（-12，-12）。这意味着两阶段囚徒困境的重复博弈结果与一次性博弈一样，是一次性博弈的简单重复。

同理，我们可以证明任意的n次有限次博弈的结果也是和两次博弈一样，也就是每个阶段的博弈结果都是（招认，招认）的纳什均衡结果。

如果我们假定博弈重复无限次，也就是说没有结束重复博弈的确定时间，即没有最后一次重复。这种情况下的博弈结果将是另外一种情况，在参与双方都采取“冷酷策略”^[9]的时候可以找到一个简单的、相互合作的完美均衡，也就是囚徒困境中的（沉默，沉默）。但是，如果参与人采用的是“针锋相对策略”，^[10]无限次重复博弈并不必然导致合作的结果。具体的分析可以参考相关的博弈论教材。