连续公共物品的私人供给

第二章　集体行动的原因——配置效率

公共选择经济学主张把配置效率的改善当做个人参与集体选择过程的重要原因之一。配置效率并不是公共选择经济学所特有的概念，在形形色色的干预主义文献中，对于配置效率的追求成为政府干预经济的一个重要理由。在那里，政府化身为追逐公共利益最大化的行为主体，这种关于国家和政府的理解恰恰是众多的公共选择经济学家所反对的。在他们看来，与市场领域中的个人相同，政治领域中的个人也同样是追逐自身利益最大化的“经济人”，“经济人”之所以选择参与集体行动，其目的也是要最大化自身利益。如果参与集体行动要比个人分散决策所达成的配置效率更高，那么，通过个人行为的相互作用，参与集体行动就能够给个人带来更大的利益。下文尝试分析存在公共物品和外部性问题时“经济人”可能做出的行为选择，力图进一步阐明，追逐更高配置效率所带来的私人利益构成“经济人”参与集体行动的一个重要原因。

第一节　离散的公共物品

公共物品指的是那种具有非排他性和非竞争性的物品。所谓排他性指的是，个人消费某一物品时能够排除其他人对于该物品的消费。所谓竞争性指的是，个人对某一物品的消费能够减少其他人对该物品可消费的数量。那些介绍西方经济学的教科书中通常会列举的公共物品有：警察与消防保护、公路、国防、灯塔、电视与无线电广播、清洁的空气等。

一、离散公共物品的私人供给

考虑一个只存在a和b两个人的简单经济，假设经济中有某一离散的公共物品G，G满足：

G=1　　当（ga+gb）≥c

G=0　　当（ga+gb）＜c　　　　　　（2.1）

其中ga和gb分别表示a和b用于购买公共物品的支出，c表示该公共物品的生产成本。

（2.1）式表明，经济中的每一个人都要考虑是否要花钱购买该公共物品，a 和b两个人用于购买公共物品的支出加总（ga+gb）决定了该公共物品的供给水平。当（ga+gb）≥c，即a和b两个人的支出加总能够弥补公共物品的生产成本时，该公共物品就能够得到供应，此时有G=1成立；当（ga+gb）＜c，即a和b两个人的支出加总不足以弥补公共物品的生产成本时，该公共物品就不能得到供应，此时有G=0成立。

假设该公共物品的生产成本为c=150元，假设a和b中的每一个人最多只愿意花费100元来购买该公共物品，有ga=gb=100元，可以用100元来衡量该公共物品的消费给每个人带来的满意程度。下面我们来分析a和b两个人就该离散公共物品的供给所展开的博弈。

如果a和b两个人都选择不购买公共物品，有ga=gb=0元，且（ga+gb）＜c，每个人都不用付出成本生产该公共物品，也不能够得到消费该公共物品所带来的好处，此时有G=0，每个人得到的利益将会是0元。

如果a和b两个人都选择购买公共物品，那么，每个人都要付出150元的成本生产该公共物品，有ga=gb=150元，且（ga+gb）>c，每个人都能够得到消费该公共物品所带来的好处，此时有G=1，因为消费该公共物品得到的好处可以用100元来衡量，每个人得到的利益将会是－50元。

如果a和b两个人中只有一个人选择购买公共物品，另一个人选择不为公共物品的生产承担任何成本，则选择购买该公共物品的个人就要付出150元的生产成本，有（ga+gb）≥c，每个人都能够得到消费该公共物品所带来的好处，此时有G=1，而消费该公共物品得到的好处只相当于100元，所以选择购买该公共物品的个人得到的利益为－50元。由于公共物品具有非排他性和非竞争性，选择不购买公共物品的个人并未付出任何生产成本，却能够得到消费该公共物品所带来的好处，因此，当存在个人选择购买该公共物品的时候，选择不购买的个人得到的利益将会是100元。学者们认为，当经济中存在为公共物品支付生产成本的个人，如果同时还存在不支付生产成本却能够免费消费该公共物品的个人，则称后者搭乘了前者的便车，并且把后者的行为选择称为搭便车行为。对于那些遵循西方主流经济学研究框架的学者来说，搭便车是他们分析集体选择问题时经常会使用的一个概念。

以上的分析可以用如图2-1所示的战略形式来描述。

图2-1　某一离散公共物品的私人供给

进一步分析图2-1所描述的静态博弈可知，对于a和b其中的任何一个人，无论其他个人选择何种战略，他都会选择不购买公共物品，可见，不购买该公共物品是a和b两个人的超优战略。又因为超优战略均衡一定是纳什均衡，所以上述博弈的纳什均衡为：（不买，不买）。因为每个人都希望搭乘对方的便车，结果却使得公共物品得不到提供，有G=0。即便考虑到a和b两个人就公共物品的供给进行无限次重复博弈的情况，每一次博弈的纳什均衡依旧是：（不买，不买）。

与图2-1描述的模型框架相类似的一些的博弈过程通常被认为是公共物品供给的分散决策模型，西方主流经济学用这些模型表示处于博弈中的个人只接受市场机制的调解，不存在政府干预的影响。但公共选择经济学却认为，即便假设只存在市场这只“看不见的手”，类似的模型也总是在暗地里引入一个集体选择的制度规则，这一制度规则能够支撑如图2-1的博弈框架。在公共选择经济学家看来，集体选择过程所遵循的制度规则其精巧性和复杂程度可以与西方主流经济学所熟知的市场机制相媲美。

二、离散公共物品的有效供给

我们把能够实现最优配置效率的公共物品数量称为公共物品的有效供给。怎样才能促使经济实现更加有效率的状态？这一问题作为一个几乎能够引发所有学者研究兴趣的传统话题，也同样吸引着公共选择经济学家的目光。但公共选择经济学更加强调，是个人的行为选择，而不是所谓的最大化公共利益的政府行为，促使经济趋向于某一更加有效率的状态。在上文分析的离散公共物品私人供给的简单模型中，如果能够通过组织某一集体行动使得经济离开由公共物品供给的分散决策所达成的纳什均衡（不买，不买），只要能够使该公共物品得到供给，令G=1，经济就会实现更高的配置效率。如果a和b两个人能够选择参与某项集体行动，共同支付150元的公共物品生产成本，他们将会得到相当于50元的剩余。在公共选择经济学家看来，正是因为有相当于50元的剩余可供彼此分享，a和b两个人才会有动力参与集体行动，进而推动具有更高配置效率的经济状态成为现实。

在图2-1所描述的某一离散公共物品私人供给的简单例子中，引入a和b两个人参与集体行动的可能性。如果个人选择参与集体行动，我们就称他的行为是合作的；如果个人选择不参与集体行动，我们就称他的行为是不合作的。

如果a和b两个人都选择不合作，我们将再一次得到图2-1所描述的分散决策模型。前文的分析表明，这一分散决策模型的纳什均衡为：（不买，不买），此时有G=0成立。因为每一个人都不会为公共物品的生产承担任何成本，也无法得到消费该公共物品所带来的好处，所以，当a和b两个人都选择不合作的时候，每个人得到的利益只能是零。

如果a和b两个人都选择合作，每一个人都要承担一部分公共物品的生产成本，令（ga+gb）=c，每一个人也都能够从公共物品的消费中得到相当于100元的好处，此时有G=1成立。因为假设该公共物品的生产成本为c=150元，所以，会有相当于50元的剩余可供a和b两个人分享，从而使得任意个人参与集体行动得到的利益大于零。关于其数值相当于50元的剩余如何在a 和b两个人中进行分配，还要看他们之间的力量对比。用ga和gb分别表示a 和b承担的成本份额，当a和b两个人都选择合作时，a得到的利益相当于100－ga，b得到的利益相当于100－gb，其中ga<100，gb<100，且（ga+gb）= 150。

如果a和b两个人中间只有一个人选择合作，另一个人选择不合作，则对于选择不合作的个人来说，如果他选择购买该公共物品，就要支付150元的生产成本，但他从该公共物品的消费中只能得到相当于100元的好处，因此，选择不合作的个人一定不会去购买该公共物品，他愿意承担的成本份额为零。对于选择合作的个人来说，因为从该公共物品的消费中只能得到相当于100元的好处，所以他不愿意承担任何超过100元的成本份额。可见，当a和b两个人中只有一个人选择合作时，有ga+gb<150。正因为选择不合作的个人不愿意支付公共物品的生产成本，从而使得选择合作的个人虽然承担了自己的成本份额，却并不能使该公共物品得到提供，此时有G=0成立。因为G=0，所以a 和b两个人都无法消费该公共物品。当a和b两个人中只有一个人选择合作时，选择不合作的个人得到的利益将会是0，选择合作的个人得到的利益相当于他所承担的成本份额，但其符号为负。

以上的分析可以用如图2-2所示的战略形式来描述。

图2-2　某一离散公共物品的有效供给

在图2-2所描述的静态博弈中，因为有ga<100且gb<100，所以a和b两个人都会选择合作，上述博弈的纳什均衡为：（合作，合作）。当a和b两个人都选择合作时，该离散公共物品将得到提供，有G=1成立。

通过进一步分析我们还可以发现，与图2-1所描述的静态博弈相比较，由于引入了合作行为的可能性，图2-2所描述的静态博弈其模型框架发生了某些关键性的变化。对于上述变化，不同学术流派的经济学家往往依靠不同的途径使之得以实现。传统的持干预主义观点的经济学家主张直接依靠政府制定的政策达成上述变化，进而帮助经济实现更高的配置效率。但公共选择经济学家却反对为政府寻找社会福利函数的做法，无论如何，公共选择经济学家认为，当经济中存在配置效率改善的余地时，个人会有动力组织并参与集体行动，以便追逐更多的私人利益，而政府不过是帮助私人达成其利益目标的机构而已。

第二节　连续的公共物品

前文讨论的是一个较为特殊的例子——离散公共物品的供给情况，下面进一步分析比较连续公共物品的私人供给和有效供给，力图从中揭示个人参与集体行动的可能性。

一、连续公共物品的私人供给

假设经济中存在某一连续公共物品G，任意个人i就该公共物品的购买数量进行选择，其中i=（1，2，…，n），n为经济中的人数，并在一定程度上代表着经济的规模。所有个人购买的公共物品数量加总决定了该公共物品的供给水平：

其中，gi表示个人i购买的公共物品数量。

任意个人i通过选择公共物品和私人物品的购买数量（gi，xi）来最大化自身效用，其目标函数可以写为：

其中，xi表示i购买的私人物品数量，gi表示i购买的公共物品数量，pg和px分别表示公共物品和私人物品的价格，mi表示i拥有的初始财富。因为公共物品具有非排他性和非竞争性，所以，任意个人i不仅能够消费自己所购买的公共物品，还能够免费消费所有其他个人购买的公共物品，i消费的公共物品数

量是经济中所有个人购买的公共物品数量之和，有而约束条件gi≥0则说明，任意个人i可以选择不购买公共物品，却不能够任意出售其他个人购买的公共物品。

经济中的所有个人就公共物品G的购买数量进行静态博弈，因为任意个人i自身的效用水平还取决于所有其他个人的公共物品购买量gj，所以，i在进行决策的时候，还要事先预测所有其他个人的选择。当gj给定，且i选择的公共物品购买量满足gi>0时，（2.3）式的拉格朗日函数可以写成：

L（gi，xi；λi）=ui（G，xi）－λi（pggi+pxxi－mi）　　　　　　（2.4）

考虑（2.4）式，如果二阶条件能够得到满足，则有下述一阶条件等于零：

由（2.6）式可知，个人i的边际替代率MRSi满足：

上述分析过程及其结论可以用i的无差异曲线和预算线来描述，如图2-3所示。

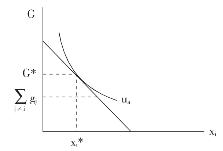
图2-3　某一连续公共物品的私人供给（a）

如图2-3所示，i会认为所有其他个人购买的公共物品数量gj太少，因此，他会选择购买某一数量gi*的公共物品，此时有gi*=G*-gj>0。

进一步整理（2.8）式，有下列不等式成立：

由（2.9）式可知，个人i的边际替代率MRSi满足：

上述分析过程及其结论同样可以用i的无差异曲线和预算线来描述，如图2-4所示。

图2-4　某一连续公共物品的私人供给（b）

如图2-4所示，i会认为所有其他个人购买的公共物品数量gj已经足够大，他的最优选择是搭便车，免费享受其他个人购买的公共物品，此时有gi* =G*-gj=0。

通过比较可以发现，（2.7）式是（2.10）式的一种特殊形式。所有个人就某一连续公共物品的供给数量进行分散决策时，任意个人i的边际替代率MRSi一定满足（2.10）式。

进一步考察上述分析过程可知，如果经济中有某一数量的公共物品得到提供，有G>0，那么，至少能够找到某一个人j，其中j=（1，2，…，n），使得j选择的公共物品数量gj*>0，且j的边际替代率MRSj满足：

通过以上过程，可以解得任意个人i的最优选择（gi*，xi*），进而得出某一连续公共物品的私人供给G*=gi*。

二、连续公共物品的有效供给

重新考虑上述连续公共物品供给的例子，如果可以使得任意个人i选择的公共物品购买数量gi和私人物品购买数量xi能够最大化经济中所有个人效用函数的加权和，也就是说，有如下形式的目标函数成立：

就能够提高整个经济的配置效率。当然，公共选择经济学强调，这种有效率的经济状态的实现还要依赖于个人追逐自身效用最大化的行为选择。

（2.12）式的拉格朗日函数可以写为：

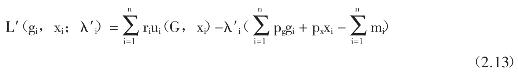
考虑（2.13）式，如果二阶条件能够得到满足，则有下述一阶条件等于零：-λ′ipg=0

由（2.14）式可以解得，任意个人i关于该连续公共物品的有效供给数量gi*′和他的私人物品购买量xi*′。进一步整理（2.14）式，有下列等式成立：

（2.15）式是保罗·萨缪尔森（1954）推得的，关于某一连续公共物品供给的帕累托最优条件。任意个人i关于该连续公共物品的有效供给gi*′能够满足（2.15）式的要求。

根据前文分析得出的结论，采用分散决策的办法解决某一连续公共物品的供给问题时，任意个人i关于该连续公共物品的私人供给gi*满足（2.10）式。并且，如果经济中有某一数量的公共物品得到提供，有G>0，那么，至少能够找到某一个人j，使得j的边际替代率MRSj满足（2.11）式。

由于求解该连续公共物品的有效供给时所使用的目标函数采取（2.12）式的形式，将（gi*，xi*）代入个人的效用函数所求得的效用加权和，不可能大于将（gi*′，xi*′）代入个人的效用函数所求得的效用加权和，其中（gi*，xi*）代表个人分散决策的均衡选择，而（gi*′，xi*′）则是（2.12）式的解。如果能够促使任意个人i选择（gi*′，xi*′），那么，与该连续公共物品私人分散决策得出的均衡状态相比较，经济中会有某一数量为正的剩余可供所有个人分享，此时，整个经济的配置效率将会得到改善。公共选择经济学认为，当存在配置效率改善的余地时，个人会有动力通过参与适当的集体选择过程，以便追求更高水平的效用。

第三节　外部性

如果某个人的行为选择能够直接影响到其他个人可实现的效用水平，我们就说，经济中存在着外部性问题。比如养蜂人饲养蜜蜂的规模可能会直接影响到相邻果园的产量；比如河流上游的化工厂决定向河水里排放污水，这可能会直接影响到河流下游居民的效用水平；再比如建筑工地的生产活动总是会产生很大的噪音，这可能会直接影响到工地附近人们的工作效率和身体健康，等等。如果某个人的行为选择能够对其他个人可实现的效用水平产生正面影响，我们就说经济中存在着外部经济。如果某个人的行为选择能够对其他个人可实现的效用水平产生负面影响，我们就说经济中存在着外部不经济。当有外部性问题存在的时候，往往就意味着经济有帕累托改进的余地。

一、存在外部性时的私人决策

考虑只存在a和b两个人的简单经济，假设该经济中只有x和e两种物品。其中，a购买x和e两种物品以求达到自身效用最大化，b只购买x一种物品以求达到自身效用最大化，但是，a关于e的消费选择会直接影响到b可实现的效用水平。则个人a的目标函数和约束条件可以写为：

个人b的目标函数和约束条件可以写为：

解以上两个有约束的最大化问题，可以得到a和b两个人关于x和e两种物品购买量的私人分散决策（xa*，ea*；xb*）。其中，（2.16）式的拉格朗日函数可以写为：

L（xa，ea；λa）=ua（xa，ea）-λa（pxxa+peea-ma）　　　　　　（2.18）

考虑（2.18）式，如果二阶条件能够得到满足，则有下述一阶条件等于零：

进一步整理（2.19）式，有下列等式成立：

个人a关于两种物品购买量的私人分散决策（xa*，ea*）满足（2.20）式。

二、存在外部性时的有效决策

重新考虑前文介绍的存在外部性问题的简单例子，如果使a和b两个人关于x和e两种物品的购买数量能够最大化他们效用函数的加权和，也就是说，有如下形式的目标函数成立：

就能提高经济的配置效率。

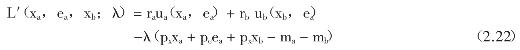
（2.21）式的拉格朗日函数可以写为：考虑（2.22）式，如果二阶条件能够得到满足，则有下述一阶条件等于零：

由（2.23）式可解得存在外部性问题时，a和b两个人关于x和e两种物品购买量的有效决策（xa*′，ea*′；xb*′），且（xa*′，ea*′；xb*′）能够使a和b两个人的效用函数加权和达到最大值。进一步整理（2.23）式，有下列等式成立：

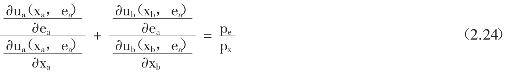
（2.24）式是存在外部性问题时的帕累托最优条件，a和b两个人关于x和e两种物品购买量的有效决策（xa*′，ea*′；xb*′）能够满足（2.24）式的要求。根据前文分析得出的结论，个人a关于x和e两种物品的私人分散决策（xa*，ea*）能够满足（2.20）式的要求。更进一步地，假设个人a的效用函数是凹的，能够满足＞0，＞0，＜0，＜0。通过比较（2.20）式与（2.24）式可知，如果a对于物品e的消费能够给b可实现的效用水平带来一定的负面影响，也就是说，经济中存在外部不经济，有＜0成立，则ea*>ea*′，xa*<xa*′；如果a对于物品e的消费能够给b可实现的效用水平带来一定的正面影响，也就是说，经济中存在外部经济，有>0成立，则ea*<ea*′，xa*>xa*′。

由于求解（xa*′，ea*′；xb*′）时所使用的目标函数采取（2.21）式的形式，将（xa*，ea*；xb*）代入a和b两个人的效用函数所求得的效用加权和，不可能大于将（xa*′，ea*′；xb*′）代入a和b两个人的效用函数所求得的效用加权和。如果能够促使a和b选择（xa*′，ea*′；xb*′），那么，与私人分散决策得出的均衡状态相比较，经济中会有某一数量为正的剩余可供所有个人分享，此时，整个经济的配置效率将会得到改善。同样地，公共选择经济学强调，当存在配置效率改善的余地时，个人会有动力参与到集体行动中来，以便追求更高水平的效用。

第四节　简单评价

公共物品和外部性作为市场失灵的重要例证，常常被经济学家列举出来用以证明政府干预经济的必要性。在以阿瑟·庇古为代表的福利经济学家眼中，政府要通过征税和提供补贴等方式来纠正外部性，借此保证公共物品的充足供给，这是对政府干预经济的一种传统解释。正像丹尼斯·C.缪勒（1989，中文1999年版，第36页）在《公共选择理论》一书中所指出的，这种传统观点常常把政府“当做像一个人，是个决策者，拥有与决定帕累托最优资源配置相关的所有信息，并宣布最优的税率和补贴”。这样一种关于政府行为的理解正是公共选择经济学家所反对的，在他们看来，只有个人才能做出行为选择，就连政府本身也不过是每一个自利的、理性的“经济人”行为选择的结果。

公共选择经济学认为，正是因为经济中存在着帕累托改进的余地，每一个“经济人”才会想尽办法提高配置效率，以便通过分配剩余来提高自身的效用水平，其中的一个重要途径就是选择与其他个人合作，通过参与某一集体选择过程达成上述目标。现实生活中的集体选择方式是多种多样的，具体采用哪一种方式得出合作的结果还取决于，处于各种集体选择方式中人们要承担的交易成本和谈判成本。一些经济学家分析比较了两种不同的集体选择方式——私人自愿遵从集体规范的行为和通过政府进行的集体选择。科斯（1960）和布坎南（1965b）等人指出，相对于大型社会而言，小规模的社会更有可能依赖私人自愿遵从集体规范的办法来达成合作的结果。曼瑟尔·奥尔森（1965）的分析也说明，在大型社会中依赖私人自愿遵从集体规范的办法会引发严重的搭便车现象，并且导致公共物品供给的不足。奥尔森认为，存在搭便车现象时要想让人们选择遵守规则，就要尽量为他们提供个性化的奖赏或鼓励。总之，按照这些经济学家的观点，在较为稳定的小型社会，利用非正式的交流渠道和精英集团的压力，就可以在很大程度上让人们自愿地遵从集体规范，并促使人们对公共物品的供给自愿作出贡献。而具有更多非人格化特征的大型社会却必须建立典型的正式惩罚制度，用以对付那些反社会的行为；建立正式的税收制度，以保证公共物品的供给；建立军队和警察制度，以保证制定和颁布的制度规则在其实施过程中能够真正得到遵守。所有这一切都要求有一个正式的政府存在。

一些公共选择经济学家对于个人参与集体选择原因的解释充分显示出他们对方法论个人主义原则的坚持，他们主张从个人行为选择入手去解释所有的社会现象，其中也包括政治领域中的诸多现象。公共选择经济学认为，当存在公共物品和外部性等问题时，依靠个人之间的合作，也就是通过参与某项集体行动的办法，要比私人分散决策更能提高个人的效用水平，因此，个人才会有动力参与到集体行动中来，并最终达到提高配置效率的结果。作为个人参与集体选择的一种方式，政府的存在会减少人数众多的大型社会为求得某一合作解而必须花费的收集信息和进行谈判的成本。可见，在公共选择经济学家看来，政府的存在，或者用本章的标题将其表述为国家的起源，其中的一个重要原因就是它能够更好地满足所有社会成员的需要，从这个角度看，政府是作为实现更高配置效率的机构而存在的。

基本概念和术语

公共物品　外部性　配置效率

思考题

您认为，公共选择经济学与传统的西方主流经济学关于公共物品和外部性问题的分析有哪些相同和不同之处？