多目标决策方法

4．多目标决策方法

4.1化多为少法

（1）线性加权和法

将多目标问题化成只有一个或两个目标的问题，然后用简单的决策方法求解，最常用的是线性加权和法。

对m个目标fi（x）分别给以权系数λi（i=1,2,…,m）,然后作新的目标函数（又称效用函数）

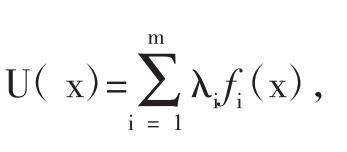
要求它越大越好。即对原来求向量极值的问题max x∈RF（X）改为求标量极值。求解新的目标函数前,先将具有不同量纲的目标值用同一尺度统一起来。一般用效用值予以统一。另一问题就是合理选择各个目标函数的权系数。

（2）平方和加权法

设有规定的m个值为f₁^*（x），f₂^*（x）,f₃^*（x）,…,f_m^*（x）要求m个函数f₁（x），f₂（x），…，f_m（x）,分别与规定的值相差程度尽量小，这时采用评价函数:

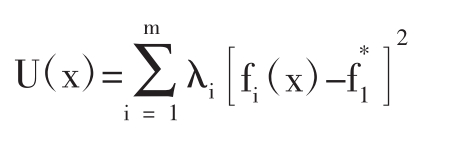
要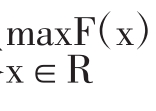其中λi可按不同要求相差程度分别给出。

4.2分层序列法

将m个目标按重要程度依次排序为f₁（x），f₂（x），…，f_m（x），先对第一个目标求最优,并找出所有最优解的集合R₀；然后在R₀内求第二个目标的最优解,找出最优解的集合R₁；如此类推，直到求出m个目标的最优解及其集合R_m-1为止，其模型为：

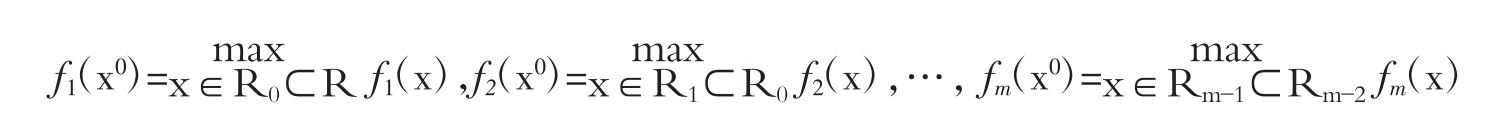
这种方法有解的前提是R₀，R₁，…，R_m-1都是非空集合，且R₀，R₁，…，R_m-2都不止有一个元素。

4.3直接求非劣解法

先求出一组非劣解，然后按事先确定好的评价标准从中找出一个满意的解。

4.4目标规划法

对于每一个目标都事先给定一个期望值，然后在满足系统一定约束条件下，找出与目标期望值最近的解。

4.5多属性效用法

各个目标均用表示效用程度大小的效用函数表示，通过效用函数构成多目标的综合效用函数，以此来评价各个可行方案的优劣。

4.6重排序法

把原来的不好比较的非劣解通过其他办法使其排出优劣次序来,以厄勒克特拉法为代表。

例2.12现举厂址选择为例,设有m个目标和n个备选方案，fj（j=1,2,…,m）为造价、运输费、燃料费、施工期限以及其他社会政治因素等各种目标，Pi为相应的目标比重，fij（i=1,2,…,n;j=1,2,…,m）为第i个方案第j个目标fj的取值（见表2.18）。

表2.18　厂址选择表

厄勒克特拉法的决策步骤是:

a.标准化{fij→yij}。由于fij的量纲不一,需要变成无量纲的yij。例如,对于要求越小越好的目标fj，先从所有目标值中找出最大值，定为最差值fiwj；找出最小值，定为最好值fiБj;并规定fiwj=1,fiБj=100;其他的yij值根据相应fij值用线性插值方法获得。

b.方案比较。由于是多目标比较，对于任何两个方案Si和Si'都会有4种可能;Si优于Si';Si劣于Si';Si等价于Si';Si与Si'关系不定,即Si与Si'均为非劣解。前3种关系的最优解可很快找到。最后一种情况的非劣解不止一个,记为{B},需进一步比较。

c.进一步比较。构造新的广义目标Z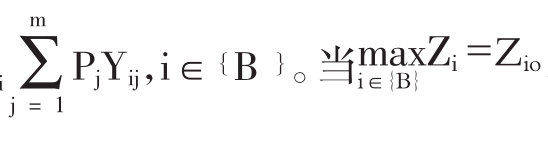，第i0方案为最优方案。