线性规划问题的解和图解法

3．线性规划问题的解和图解法

3.1线性规划问题的解

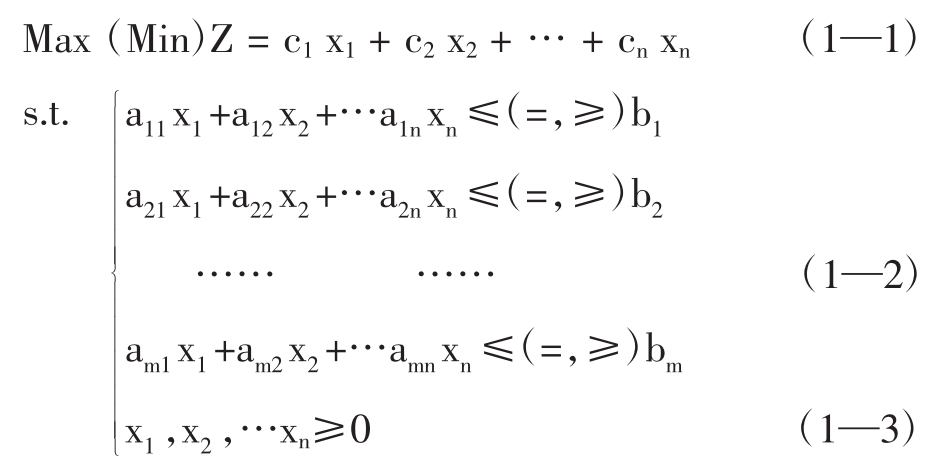
称满足式（1—2）的点X（或向量）为该问题的解（solution）；若其同时又是式（1—3）的解，则称点X为可行解（feasible solution）；所有可行解组成的集合称为可行域（feasible region）或可行解集。可行域上满足式（1—1）的点称为最优解（optimal solution），最优解对应的目标函数值称为最优值。

3.2线性规划的图解法

对于只有两个决策变量的线性规划问题，可以在平面直角坐标系上作图求解，同时可以直观地理解线性规划问题解的几何意义。

例3.8求解

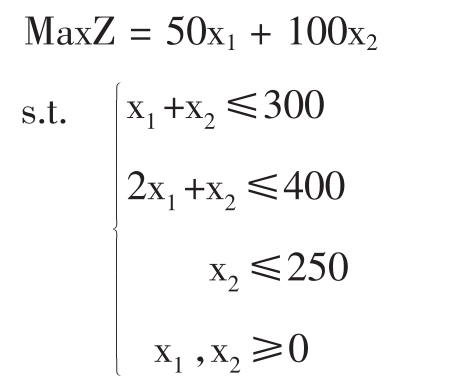
解：由约束条件首先画出可行域。

因为x₁，x₂≥0，可行域在第一象限。第一个约束条件x₁+x₂≤300表示半平面，此半平面是以直线x₁+x₂=300为边界的右下方第一象限部分（见图3.1）。类似地可求出其余约束条件表示的半平面部分（见图3.1）。图中的凸多边形OABCD即为可行域。

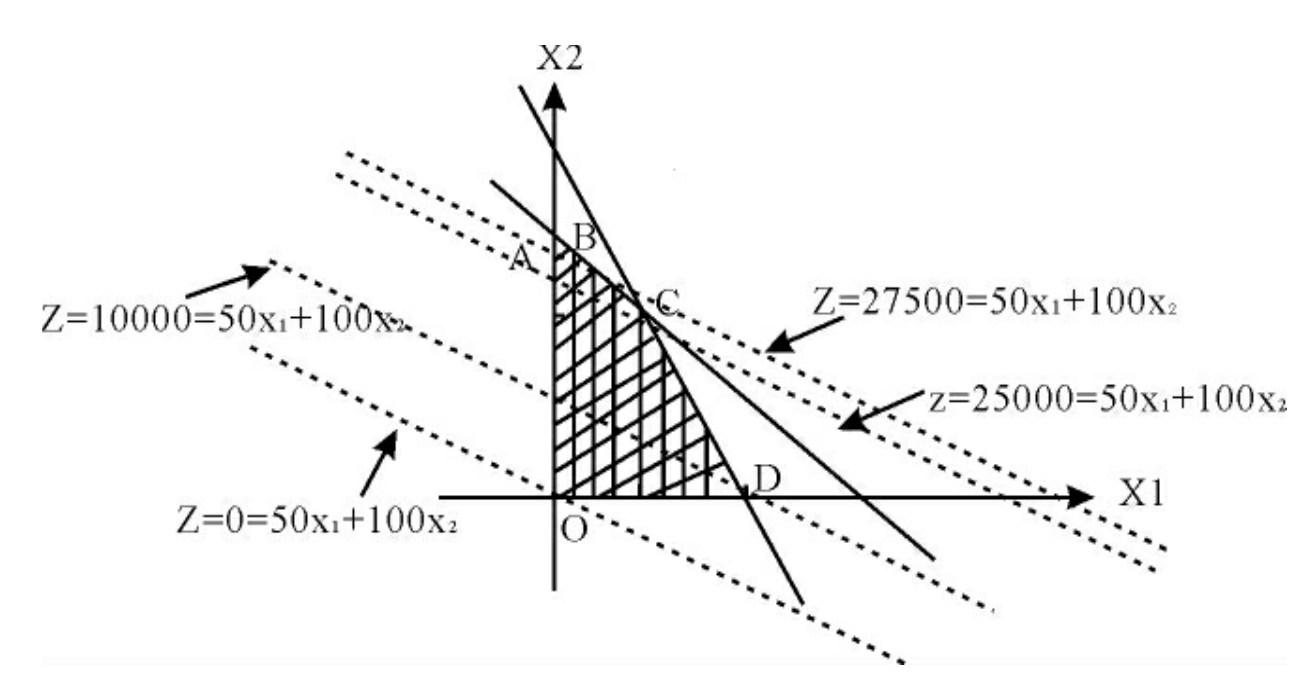
图3.1

其次，考虑目标函数的等值线和梯度方向。

对于Z=50x₁+100x₂，则50x₁+100x₂=C表示目标函数取值为的一簇平行直线，称为等值线。由微分学得知，由x₁和x₂的价值系数为分量组成的列向量（c₁，c₂）^T=（50，100）^T，即为z的梯度方向（见图3.1）。等值线沿梯度向右上方平移，目标函数z值增加最快。反向平移则减少最快。

现在求最优解。任画一条初始等值线，如图中的直线。由于是求z的最大值，所以沿梯度方向平移至可行域的切线位置L处．则切点B即为最优解。

求出B点坐标：

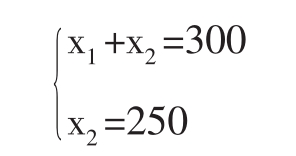
得x₁^*=50，x₂^*=250

最优值为Zmax=50×50+100×250=27500

若本题是求minZ，则最优解在O点处达到，其最小值Zmin=0。

例3.9求解

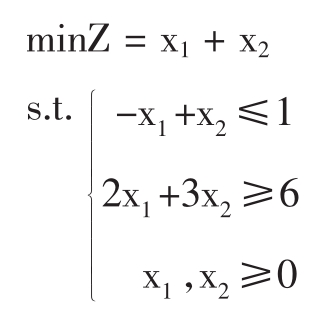
解：由图3.2可知可行域无界，最优解为x₁^*=3/5，x₂^*=8/5，即A点，最优值Zmin=3/5+ 8/5=11/5。

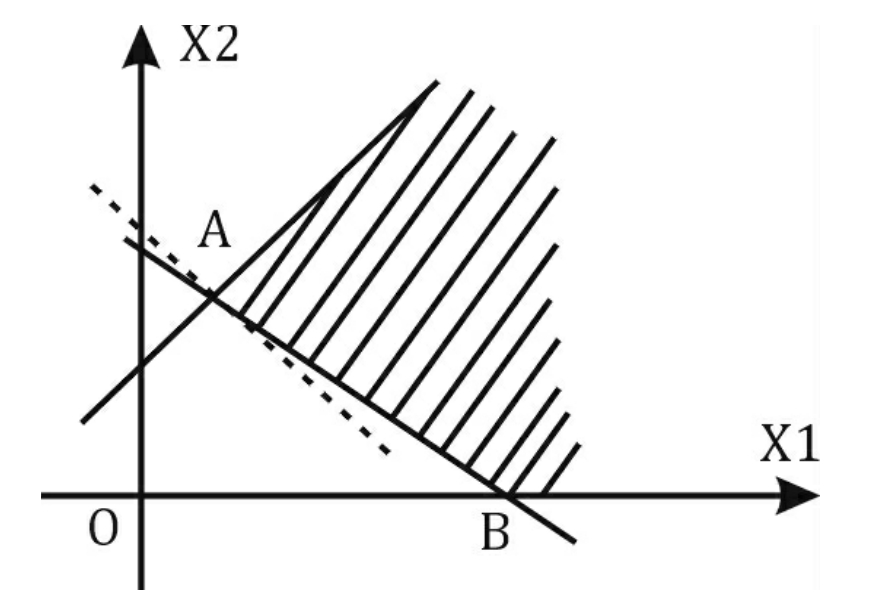
图3.2

若求maxZ=x₁+x₂，则等值线沿梯度方向（1，1）^T可无穷平移，与可行域总有交点。当在可行域内求maxZ（或minZ），而目标函效z无上界（或无下界）时，称该问题无最优解。但在实际问题中，一般只有在模型建立有误时才可能出现这种情况。

若求minZ=2x₁+3x₂，则AB线段上的点都是最优解。这种有无穷多最优解的情况，称该问题有多重最优解。

例3.10求解

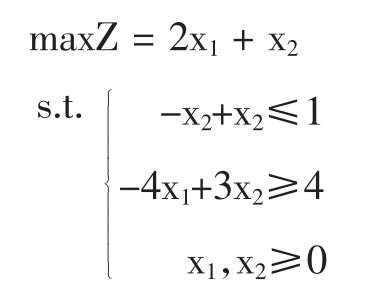
解：前两个约束条件在第一象限没有公共部分，所以无可行解，自然也就没有最优解。

通过上述几个例子，对线性规划问题解的几何意义有了初步了解，并可得出以下两个重要结论：

①可行域如果存在，它可能是一个凸多边形，也可能是无界的。

②最优解如果存在，必在可行域的某一顶点上取得；若在两个顶点上都得到最优解，则这两点所连线段上所有点都是最优解。

上述两个结论也是线性规划问题最基本的性质。我们可以在更一般的情形下加以证明。

总之，对于一个LP问题，需要对下列情况进行判断分析：一是可行域不存在（或说可行解集是空集），这时该问题无解或无可行解。二是可行域无界，这时如果目标函数无界，则该问题无最优解；如果目标函数有界，则问题有最优解。三是可行域有界，且最优解存在时，则该问题可以有唯一的最优解或有多重最优解。