使用两个可变投入要素的生产

第四章　生产理论

第一节　生产函数

一、生产与厂商

所谓生产，就是一切能够创造或增加效用的人类活动。生产可以分为两大类：第一类是生产有形产品，比如生产粮食可供人们充饥，生产衣服可供人御寒，将面粉加工成各式各样的食品，可以提供给消费者巨大的满足。总之，凡从原始产品到最终产品之间的所有物质创造都是生产活动。第二类是生产无形产品，即服务的生产。例如车船运输，能创造把货物或人从一个地方运往另—个地方位置变化的效用；把贵重物品交银行保管，或把易腐变质的食品、药品存于冷库，待以后需要时取出应用，能创造时间推移的效用。所有诸如此类的活动，如理发、看病、教育、音乐演奏、街道清扫、警察提供安全，等等，都是生产活动。

西方经济学中把生产活动的主体称作厂商。而厂商被认为具有经济理性，追求利润最大化目标。

二、生产的三要素

任何生产均需要投入各种不同的生产要素。西方经济学家把生产要素分为三类：

1．劳动

劳动包括体力劳动和脑力劳动。劳动不是指劳动者本身指劳动者提供的服务。劳动的价格是工资。

2．土地

西方经济学所讲的土地是一个广义的概念，不仅包括土地，还包括河山、森林、能源、矿藏、原料等一切自然资源。土地的价格是地租。

3．资本

资本指生产过程中使用的各种生产设备，如机器、厂房、工具、仓库等，并不是专指货币。货币本身并不能用于生产活动。但是有了货币后就能购买到机器、设备，所以经济学上不对它们加以区别。资本的价格是利息。

以上是西方经济学传统的“生产的三要素”说。后来，马歇尔在其《经济学原理》一书中，又增加了一种生产要素——企业家的才能，其价格就是利润。因此，“生产的三要素”说便发展为“生产的四要素”说。

三、生产函数

任何生产过程都需要投入各种不同的生产要素，在一定的技术水平下，生产出来的产品数量取决于所使用的生产要素数量的多少以及它们之间的相互配合状况。生产函数就是表示生产要素的某种组合同它可能生产的最大产量之间的关系。生产函数一般采用列表、图形或数学方程式表示。例如，用Q代表某种产品的产量，L、K、N、E等分别代表劳动、资本、土地、企业家才能这四种生产要素，则生产函数的一般形式可写成：

Q＝f（L，K，N，E）

式中，L，K，N，E等为自变量，Q为因变量，方程式的含义是：在一定的技术水平条件下，假如L，K，N，E等各种生产要素的投入量已知，那么就可以知道某种产品的最大产出量Q。反之，假如Q为已知，那么也就可以知道L，K，N，E等各种投入要素的最低限度量。

生产函数的概念的两个性质：

（1）在既定的技术水平下，如果各种生产要素的数量增加，产出量也随之增加。因此产出量是各生产要素的增函数。如果发生了技术进步，生产函数本身就会改变，假如技术进步提高了劳动生产率，那么要得到与原先一样多的产量，所必须投入的劳动量将会减少。

（2）生产函数表示的产出量是最大的。生产函数，依据一定的划分标准，可以形成一定的分类。根据各种生产要素投入比例是否可以变动，生产函数可分为可变比例生产函数与固定比例生产函数。在有些生产过程中，要素投入比例，例如劳动与资本投入数量的比例，是可以变的。可以多用一些劳动，少用一些资本；也可以少用一些劳动，多用一些资本。反映这种生产过程中要素投入量与产出数量之间关系的生产函数就称为可变比例生产函数。如果生产中各种要素数量比例是固定不变的，劳动增加了，资本也一定要按比例增加，这种生产函数就是固定比例生产函数。

四、短期与长期

生产不仅需要劳动和土地，而且还需要时间。输油管道不可能在一夜之间就建造起来，而一旦建成，就要持续地运用几十年的时间。农民不可能在一个季节当中改种作物。一座大型发电厂的设计、建造、测试和调试并交付使用往往需要10年的时间。另外，资本设备一旦以一种具体的形式投入到一个巨大的汽车装配工厂，如果要拆卸并搬到另一地方或转入他用，那么在经济上就不合算了。

这里的短期、长期，不是指一个具体的时间跨度，而是指能否使厂商来得及调整生产规模（固定的生产要素和生产能力）所需要的时间长度。“长期”是指时间长到可以使厂商调整生产规模来达到调整产量的目的；短期则指时间短到厂商来不及调整生产规模来达到调整产量的目的，而只能在原有厂房、机器、设备条件下依靠多用或少用一些人工和原材料等来调整产量。例如，某产品市场需求量由于某种原因暂时扩大时，厂商可通过充分利用原有设备，开足马力，加班加点来增加产量以满足需求，这就是短期调整产量水平的问题。相反，如果市场对该产品的需求是由于人们对这种产品偏好普遍变大而长期地增加，则厂商要增加设备扩大生产规模来满足增长了的市场需求。这就是长期调整生产的问题。

可见，在长期中，一切生产要素都是可以变动的，不仅劳动投入量、原材料使用量可变，而且资本设备量也可变。而在短期中，只有一部分要素如劳动投入量及原材料数量是可变的，称为可变投入，即在短期内投入量随产出量的变动而变动的要素。而另一些生产要素不随产量的变动而变动，如机器、设备、厂房、高级管理人才等，称为固定投入，即在短期内投入量不随产出量的变动而变动的要素。

第二节　使用一种可变投入要素的生产——生产的三阶段

生产中两种最重要的投入是劳动与资本，因此，在经济分析中，通常假定企业只使用这两种要素。在短期内，假设资本数量不变，只有劳动可随产量变化，则生产函数可表示为Q＝f（L），这种生产函数称为短期生产函数；在长期内，资本和劳动都可变，则生产函数可表示为Q＝f（L，K），这种生产函数可称为长期生产函数。本节分析短期中即使用一种可变投入要素时厂商的合理区间。

一、总产量、平均产量和边际产量

厂商生产某一特定产量的成本不仅取决于所需生产要素的价格，还取决于生产这一产量所需生产要素的数量。

总产量（Total Product）是投入一定量的某种生产要素所生产出来的全部产量，简写为TP。

TP＝f（L）

平均产量（Average Product）是平均每单位某种生产要素所生产出来的产量，简写为AP。

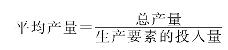
AP＝TP/L

边际产量（Marginal Product）是增加一单位某种生产要素所增加的产量，简写为MP。

或

我们假定只有一种可变要素投入，生产一种产品，生产函数的具体形式设为：Q＝f（L）＝27L＋12L2－L3（即可变的投入要素为劳动L），则劳动的平均产量用AP表示为：

AP＝TP/L＝27＋12L－L2

劳动的边际产量表示为：

MP＝dTP/dL＝27＋24L－3L2

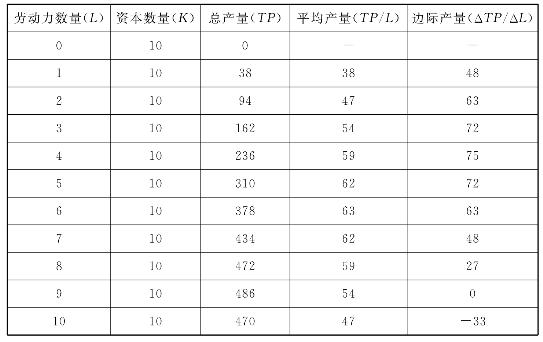
根据上边的计算式，投入的劳动量与总产量、平均产量和边际产量可用表4－1表示。

表4－1　总产量、平均产量和边际产量

二、总产量、平均产量和边际产量曲线

根据上表，可以绘出总产量、平均产量和边际产量曲线，见图4－1。图4－1中的三条产量曲线是指一定技术水平条件下的投入产出关系。前面说过，生产函数中的投入产出关系，取决于技术水平。如果技术进步了，采用了更先进的设备，同样投入这些劳动，会产出更多产品，于是这三条产量曲线都会向上作相应移动。它表明劳动生产率提高了。先进技术的采用，可使生产中的每一劳动小时，每一吨煤，每一度电，每一立方米的水等等生产资源创造出更多产品来。如果劳动者素质提高，管理改进，可使每单位资本有更多产出，就是说资本生产率大大提高。现在我们仍旧来考察既定技术水平上的产量曲线。

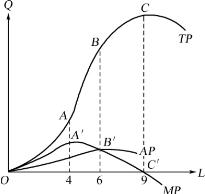
图4－1　产量曲线

从表4－1、图4－1中可以看到：

（1）随着劳动量的增加，最初总产量、平均产量和边际产量都是递增的。

（2）当劳动量增加到4个单位时，从边际产量曲线MP线可以看出，这时MP达到最大，即在A′点，最大的MP＝dTP/dL＝75。

（3）当劳动量增加到6个单位时，平均产量达到最大，为MaxAP＝63，这时边际产量也为63，可见当AP＝MP时，即在图上点B′点，平均产量达到最大。

（4）当劳动量增加到9个单位时，总产量达到最大，为TP＝486，这时边际产量为0，即dTP/dL＝0。这时，若再增加劳动量（如第10个单位），不会带来总产量的增加，而只会使总产量减少。

由上边的分析，对照图4－1、表4－1，我们进一步分析这三个产量之间的关系。

（1）总产量和边际产量的关系。边际产量曲线是总产量曲线上各点的斜率值曲线。因此，总产量斜率值最高的一点，即拐点（图中A点），与其横坐标相等的点便是边际产量曲线上的最高点，见图中A′点。当MP＞0，TP是增加的，总产量曲线的最高点（图中C点），边际产量曲线上与其横坐标相等的点（图中C′点），这时的边际产量为零。当MP＜0，TP是下降的。

（2）总产量与平均产量的关系。平均产量曲线是总产量曲线上各点与原点连线的斜率值曲线。因此，其斜率值最高的一点，即通过原点所作直线与总产量曲线的切点（图中B点），与其横坐标相等的点便是平均产量曲线上的最高点，见图中B′点。

（3）平均产量与边际产量的关系。平均产量曲线的最高点，一定是平均产量曲线与边际产量曲线的交点（即图中B′点）。因为当边际产量等于平均产量后，再往下递减时，平均产量也下降。平均产量曲线上升的部分，边际产量曲线一定高于平均产量曲线。两条曲线相交后下降的部分，边际产量曲线一定低于平均产量曲线。

三、边际收益递减规律

从上述投入劳动量L的变动对总产量、平均产量和边际产量的影响中可见，在开始阶段劳动的边际产量随劳动量的增加而增加，即边际产量处于递增阶段；但当L＝4以后，即边际产量处于递减阶段，这时总产量以递减的比率上升；当L＝9时，边际产量为0，总产量最大；此后若再增加劳动L的投入，总产量反而逐渐减少。之所以发生这种情况，是由于固定投入的生产要素有一个容量问题。在L＜4时，固定投入和可变投入的配合比例不当，固定要素显得太多，而可变要素显得太少。比方说，一个工厂里有机器10台，假定至少要有20个操作工人，但只有15个工人。这时增加可变要素，人的边际产量递增。当L＝4时，两者配合的比例最适当，边际产量达到最大。但当L＞4时，由于固定要素的容量有限，可变要素增加时，又使两者比例失调，可变投入显得太多，固定要素显得不足。这时边际产量会递减，总产量虽然增大，但是以递减的比率上升的。当L＝9时，边际产量为0，即可变要素已开始超过固定要素要求的比例，如再有劳动量的投入，不会带来总产量的增加，比方再投入第10个劳动量，不仅不增加总产量，而且总产量会递减，这时的边际产量为负值。类似地，给一块一亩地庄稼施肥，开始随着肥料的增加，土壤结构得到改善，增加了其肥力，产量会以递增的比率上升；若不断增加施肥到一定程度，肥力过大，超过麦苗的需要，产量不仅不能增加，反而会下降。

综合上述，我们可以得出如下一条规律：在一定技术水平条件下，若其他生产要素不变，连续地增加某种生产要素的投入量，在达到某一点之后，总产量的增加会递减，即产出增加的比例小于投入增加的比例，这就是生产要素报酬递减规律，亦称边际收益递减规律。

边际收益递减规律要发生作用必须具备三个前提条件：

第一，生产要素投入量的比例是可变的，即技术系数是可变的。这就是说，在保持其他生产要素不变而只增加其中某种生产要素投入量的时候，要素边际收益才发生递减，如果各种生产要素的投入量按原比例同时增加时，边际收益不一定递减。

第二，技术水平保持不变。如果技术水平提高，在保持其他生产要素不变而增加某种生产要素时，边际收益不一定递减。

第三，所增加的生产要素具有同样的效率。如果增加的第二个单位的生产要素比第一个单位的更为有效，则边际收益不一定递减。

四、生产的三阶段

根据总产量曲线、平均产量曲线和边际产量曲线的形状，可以进一步分析生产的三阶段。将上述三条曲线合并在一张图上，见图4－2。

图4－2　生产三阶段

从图中可以看出：

第一阶段：平均产量递增阶段，即平均产量从零增到平均产量的最高点B′。这一阶段是从原点到曲线AP和MP的交点。

第二阶段：平均产量递减，但边际产量仍大于零，所以总产量仍然递增，直到总产量达到最高点C点。这一阶段是从曲线AP和MP的交点到曲线MP和横坐标的交点C′点。

第三阶段；边际产量为负值，总产量也递减。这一阶段是曲线MP和横坐标的交点C′以后的阶段。

上述三阶段的划分，不仅说明由于边际收益递减规律的作用，总产量、边际产量、平均产量都是先增后减的，而且还说明了厂商进行生产要素投入的合理阶段。

假如厂商不考虑单位产品的成本，而希望得到最大的产量，那么某一生产要素的投入量以C′为最合适，因为这时总产量最大。

假如厂商考虑单位产品的成本，不要求得到最大产量，那么某一生产要素的投入量以B′为最合适，因为这时平均产量最大。

但无论如何，厂商肯定不会在第三阶段生产，因为这个阶段的边际产量为负值，生产不会带来任何好处。厂商也不会在第一阶段生产，因为平均产量仍可以增加，投入的这种生产要素还未发挥到最大作用，厂商没有获得可以获得的更多的好处。因此，厂商只会在第二阶段生产，因为虽然在这一阶段平均产量和边际产量都下降，但总产量还在不断增加，收入也增加，只是增加的速度逐渐缓慢，直到停止增加为止。

第三节　使用两个可变投入要素的生产

一、等产量曲线

上一节讨论了只有一个可变投入要素时的一些基本情况，现在进一步讨论使用两个可变投入要素并且这两种要素存在替代关系时的情况。为了图形分析上的方便，只假设有两种生产要素的投入，但分析的结果对两个以上的可变投入也是适用的，因为既可以假定这两个投入是可变的，也可以假定这两个投入中的一个代表所有其他可变投入的组合。

假定生产函数中只有两种投入要素，其他生产要素的数量均保持不变，总产量也保持不变。以Q代表总产量，L和K分别代表两种投入要素，这两种生产要素数量与产量之间的关系可用下述函数形态表示：

Q＝f（L，K）

该生产函数中，K和L两种生产要素具有一定程度的互相替代关系，即增加对K的使用量，同时减少L的使用量，可以使总产量不变。在总产量不变的情况下，劳动和资本的各种可能的数量组合如表4－2。以L代表劳动，K代表资本，I代表等产量曲线，作出相应的图形，如图4－3。

表4－2

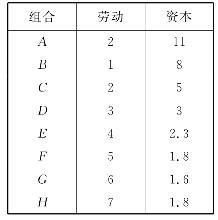
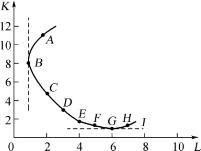
图4－3　等产量曲线

表4－3中的等产量曲线表示资本和劳动的不同数量组合能够生产出同等数量的产品，也就是等产量曲线上各点的产量都相同。图4－3从B点到G，依次表示劳动投入量不断增加，而资本投入量不断减少，两种生产要素的投入量之间存在此消彼长的替代关系。厂商可以在这个区间选择合适的组合。如果希望多用资本少用劳动，就可选择C点的组合；如果希望多用劳动少用资本，就可选择E 或F点的组合。图中A点至B点和G点至H点的两段曲线都是正斜率的。它们表示，由于过度使用一种要素以后，为了减少过度使用带来的危害，必须相应追加另一种要素，以便使产量保持不变。虽然B点右上和G点右边的两段曲线，也表示两种要素的下同数量组合与相同产量之间的关系，但是，这种关系不是生产的技术要求决定的，也是不经济的，厂商也不会自愿地选择处于这个区域。所以有实际意义的等产量曲线是从图4－3中B点到G点的曲线。

等产量曲线与无差异曲线很相似，其基本性质也相同。即

（1）受边际收益递减规律的作用，等产量曲线是凸向原点的。

（2）不同的等产量曲线之间不能相交。

（3）位置越高的等产量曲线表示的产量水平越高。

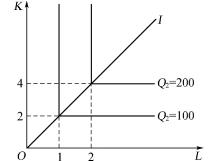
图4－4　固定技术系数的等产量曲线

假定用于生产的两种可变要素不能相互替代，那么等产量曲线的形状与上述不同，变成直角折线。例如，若资本和劳动的投入按2∶1的固定比例使用，生产100单位的产量必须投入2单位的资本和1单位的劳动，生产200单位的产量必须投入4单位的资本和2单位的劳动。要是资本为2单位，劳动小于1单位，则资本无法充分发挥作用。在这种固定比例的情况下，等产量曲线表现为图4－4所示的形式：连接原点与每一等产量线的直角顶点的连线的斜率为固定技术系数。

图4－4说明假如劳动与资本的投入只有一种增加，一种不变，则增加的劳动或资本的边际产量为零。只有两者同时同比例增加，产量才能按比例地增加。

如果两种投入的要素可以完全替代，则等产量曲线为一条向右下倾斜的直线（图略）。

二、生产要素的边际替代率

在等产量曲线的斜率为负值的前提下，在两个变动投入的生产要素中，以一种生产要素替代另一个生产要素而保持产量不变替代比率，就叫做“生产要素的边际替代率”。

假如有X和Y两种生产要素，并且用X代替Y，则X要素对Y要素的边际替代率可以用下述公式表示：

MRSXY：X要素对Y要素的边际替代率；

ΔX：X要素的变化量；

ΔY：Y要素的变化量。

现在仍以表4－2举过的例子来计算劳动对资本的边际替代率。从表4－3中可以看出，劳动和资本在处于负向变化关系时（即劳动减少，资本增加；或资本减少，劳动增加），两者有替代关系。当劳动的使用从1单位增加到2单位时，资本的使用从原来的8单位减少到5单位，即减少了3单位。这时MRSXY＝3。

表4－3　生产要素的边际替代率

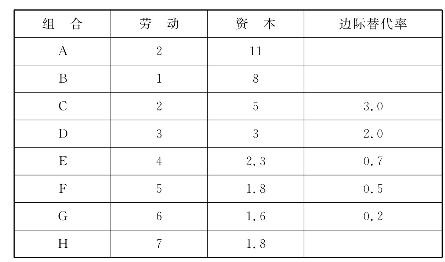
生产要素的边际替代率就是等产量曲线上的斜率。如果要计算等产量曲线上某一点的替代率，就是过该点做一条切线的斜率值。以横坐标代表劳动L，以纵坐标代表资本K，则劳动对资本的边际替代率等于dK/dL。

从表4－3中还可以看出，如果不断地用劳动代替资本，则劳动对资本的边际替代率越来越小。例如，劳动的使用从1单位增加到2单位时，资本的使用从8单位减少到5单位，边际替代率为3。当劳动的使用从2单位增加到3单位，资本的使用从5单位减少到3单位，边际替代率为2。当劳动由3单位增至4单位，资本由3单位下降到2．3，边际替代率为0．7。以此类推，劳动对资本的边际替代率进一步下降为0．5、0．2。如果从等产量曲线来看，则反映为曲线的斜率越来越小。

造成边际替代率下降的原因是：随着劳动越来越多地被使用，其边际产量则越来越少；而随着资本的越来越少，其边际产量越来越多。如果反过来用资本代替劳动，情况也一样。因此可以得出结论如下：在一条等产量曲线上，当一种生产要素不断地代替另一种生产要素时，其边际替代率是递减的。

因为等产量曲线的边际替代率递减，所以等产量曲线都是凸向原点的曲线。这一特点同无差异曲线一样。

仍以劳动和资本为例，边际替代率与两个生产要素的边际生产量有这样的关系：以劳动替代资本的边际替代率，等于劳动的边际产量与资本的边际产量的比。公式为：

MRSLK：用劳动替代资本的边际替代率；

MPL：劳动的边际产量；

MPK：资本的边际产量；

dL：劳动的变化量；

dK：资本的变化量。

上述关系的说明如下：要维持产量不变，增加劳动所造成的生产量的增加，必须等于减少资本所造成的生产量的减少。

上述关系的数学证明如下：以TP代表某一条等产量曲线的固定产量，其生产函数为TP＝f（K，L）。全微分结果为：

即

所以

从公式中也可明显看出，当不断用劳动（L）代替资本（K）时，由于劳动的边际产量（MPL）的值不断减少，而资本的边际产量（MPK）的值不断增加，因此劳动对资本的边际替代率（MRSLK）不断下降。

三、等产量线的脊线和生产区域

等产量曲线的斜率可以为负值，也可以为正值。当等产量曲线斜率为负值时，表明两种生产要素可以互相替代，一种要素减少，另一种要素增加。图4－3中B点到G点的曲线都属于这种情况。

当等产量曲线斜率为正值时，表明两种要素必须同时增加才能维持总产量不变。这就是说，其中一种生产要素的投入量已达饱和状态，再继续使用这种要素时，其边际产量反而为负值，这时不得不靠增加另一种要素的投入量加以弥补，才能保持总产量不变。例如化肥的过多使用造成农产品产量减少，增加劳动可以弥补所造成的损失。图4－3中B点至A点曲线以及G点到H点曲线，均属于这种情况。

等产量曲线的斜率还可能为零或无穷大。如图4－3中，经B点与纵坐标平行的切线，其斜率为无穷大；经G点和横坐标平行的切线，其斜率为零。这两种情况表明两种要素之间完全不能替代。

以上仅介绍一条等产量曲线，实际上，等产量曲线可以作出无数条。每一条曲线上所表示的总产量相等，不同曲线之间在总量上不等。等产量曲线的位置越偏离原点，所示表示的总产出量就越大。图4－5中有三条等产量曲线，I3的产量小于I2的产量，I2的产量小于I1的产量。

图4－5中A、B、C各点和A′、B′、C′各点可看成是一个界限，超过这个界限，则必须同时增加两种投入要素的数量，才能使总产量不变。把A、B、C各点和A′、B′、C′各点连接起来所形成的两条线，称为“脊线”。“脊线”表明生产要素替代的有效范围。实际上，厂商是不会在“脊线”以外的范围从事生产的。厂商可以在两条“脊线”所形成的区域以内从事生产，任意变动其投入要素的组合。因此，这一区域称为“生产区域”。

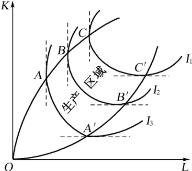
图4－5　脊线

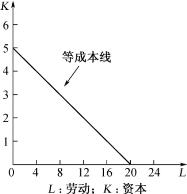
图4－6　等成本曲线

四、等成本线

假如已知两种生产要素的价格和生产者用来购买这两种生产要素的支出，那么，就可以求出购买这两种生产要素的“等成本线”。等成本线就是表示相等的成本可购买的各种投入要素的不同组合。

仍以劳动和资本为例，假设资本的价格为＄4，劳动的价格为＄1，生产者用于购买这两种生产要素的金额为＄20，则很容易作出一条等成本线，如图4－6所示。

等成本线的做法和消费者预算线的做法完全相同，只不过在内容上稍有差别。等成本线的斜率也和预算线一样，为横坐标所代表的投入要素的价格同纵坐标所代表的投入要素的价格之比。按照西方经济学家的观点，劳动的价格是工资，资本的价格是利息，以W代表工资，R代表利息，则上述等成本线的斜率为－W/R。以M代表生产者用于购买生产要素的支出，上述等成本线可用公式表示如下：

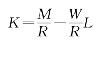
其中，为纵坐标上的截距；为等成本线的斜率。其求法完全同于预算线的求法，其规律也完全同于预算线的规律。假如两投入要素的相对价格发生变化，则等成本线的斜率也发生变化。等成本线也可以有许多条，这取决于生产者用于购买生产要素的金额数量多少以及两个投入要素的价格水平状况。

五、生产者均衡

把上面介绍的等产量曲线和等成本曲线放在一起考察，可以分析出“生产者均衡”。所谓“生产者均衡”，是指生产者使用一定的经费而获得最大的产量。生产者均衡和消费者均衡类似，只不过消费者均衡是指用有限的收入获得最大的效用。

将等产量曲线和等成本曲线放在一起的图形如图4－7所示。

图4－7中，I1、I2和I3分别代表三条不同的等产量曲线，K1L1代表生产者在一定经费下的等成本线。显然，生产者不可能达到I3的产量水平。生产者可以达到I1的产量水平，例如在A或B点组合进行生产。但是，这种组合并没有使产量最大化，沿着等成本线从A点朝E点靠近、或从B点朝E点靠近，都可以在同样经费支出情况下获得更多产量。越靠近E点，产出量越大，到达E点，产量最大化。E点为等产量曲线和等成本线相切的一点。这一点就是生产者均衡点。从图中可看出，生产者最佳的投入组合为OLE单位的劳动和OKE单位的资本。

上面讲的是生产者使用一定的经费而获得最大的产量。生产者均衡还可以从另一个角度来考察，即生产者在一定的产量中寻求最小的投入成本。这可以从图4－7中看出。

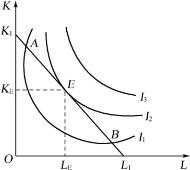
图4－7　成本既定时，产量最优

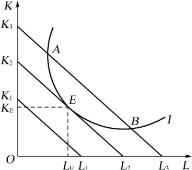
图4－8　产量既定时，成本最低

图中表示，在既定的劳动和资本价格水平下，等产量曲线I可以根据三条等成本线进行选择。要达到I所代表的生产量水平，选择哪一种投入组合才能使成本最小？显然，生产者只能选择成本线K2L2。任何低于K2L2的等成本线，如K1L1，是不可能使生产达到I所代表的水平的。任何高于K2L2的等成本线是不足取的，因为不符合成本最小化原则。例如生产者开始误选了K3L3等成本线，寻找出A点和B点两个组合点，他将很快发现应当沿着等产量曲线I向下或向上移动，一直到E点。E点是最佳投入要素组合点，即生产者均衡点。在E点，生产者应当购买OLE的劳动以及OKE的资本。

上述两种情况都说明了：生产者均衡使一定的成本得到尽可能高的产出水平，或者使一定的产出水平只付出尽可能低的成本。总之，生产者均衡意味着资源的最佳配置。

生产者在许多情况下都要面临着成本最小化的选择。现在进一步研究按“成本最小化原则”进行投入要素的定量计算。

假设某厂商只使用劳动（L）和资本（K）两种投入要素。其生产成本最小化的条件是：

公式中，MPK代表资本的边际产量；MPL代表劳动的边际产量；PK代表资本的价格；PL代表劳动的价格。公式中的含义十分清楚，只要花在资本K的每个单位的钱所产生的边际产量大于花在劳动上所产生的边际产量，就应当用资本代替劳动。反过来，如果花在劳动上的每个单位的钱所产生的边际产量大于花在资本上所产生的边际产量，就应当用劳动代替资本。公式又可变为：

是最后一个单位的资本和劳动的产出比较。假如该比率等于4，即意味着多用一个单位的资本是多用一个单位的劳动的产出的4倍。则为多用一个单位的资本与多用一个单位的劳动的代价比率。如果该比率也等于4，则资本和劳动不必互相代替。因为虽然资本边际产出量是劳动边际产出量的4倍，但是其代价也是4倍。如果该比率等于2，说明虽然资本的价格2倍于劳动的价格．但其产出量却为劳动产出量的4倍，所以仍然可用资本代替劳动。如果该比率等于6，说明资本的价格6倍于劳动的价格，而产出量仅4倍于劳动的产出量，因此这时需要用劳动代替资本。

上述原则就是经济学上的“替代原则”。如果生产要素的相对价格发生变化，生产方法也将随之而变，相对地多用那些便宜的投入要素而少用那些昂贵的要素。

此原则的重要意义在于，如果一个国家土地广阔而入口稀少，土地价格就低，而劳动的工资率必高。在农业生产上应当采用较多地使用便宜的土地而最经济地使用劳动的做法。其生产应采取劳动和土地低比率的方式。反之，如果另一个国家土地少，而人口众多，在农业生产上应采用在每单位土地上多使用劳动的方 法。其生产应采取劳动和土地高比率的方式。这一原理可以说明为什么生产同一种产品，不同的国家采用不同的方式。例如美国等西方发达国家，劳动的价格高，生产时便采用资本密集型方式；而许多发展中国家劳力资源丰富，便采用劳动密集型方式。

六、生产扩展线

如果厂商的经费支出增加，则他想扩大生产要素投入以增加产量。这就是生产扩展的概念。

生产扩展线表示在生产要素价格、生产技术和其他条件不变的情况下，企业扩大生产规模所引起的生产要素最优组合点移动的轨迹。

如果生产要素价格不变，厂商的经费支出增加，等成本线会平行地向上移动；如果厂商改变产量，等产量线也会发生平移。这些等产量曲线将与相应的等成本线相切，形成一系列生产者均衡点，把所有这些点连接起来形成的曲线叫做生产扩展线。图4－9中的曲线OE就是一条生产扩展线。由于生产要素的价格保持不变，生产者均衡约束条件又是MRSLK＝，所以生产扩展线上的所有的生产均衡点的边际技术替代率相等。在生产扩展线上，可以用最小成本生产最大产量，从而获得最大利润，所以厂商愿意沿此路径扩大生产，虽然其他路径也能达到使产量扩大的结果，但都不是最优路径，只有沿均衡点扩大规模才是最优路径。但厂商究竟会把生产推进到生产扩展线上的哪一点上，单凭生产扩展线是不能确定的，还要看市场上需求的情况。

图4－9说明了这种情况。

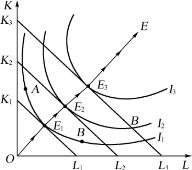
图4－9　生产扩展线

七、柯布—道格拉斯生产函数

在20世纪30年代初，美国经济学家P．道格拉斯与C．柯布根据美国1899—1922年的工业生产统计资料，得出了这一时期美国的生产函数为：

Q＝ALαK1－αKβ

这就是经济学中著名的“柯布—道格拉斯生产函数”。在这个生产函数中α 与β为常数，其中0＜α＜1，0＜β＜1。

当α＋β＝1时，Q＝ALαK1－α。

美国20世纪初期的经验数值

这表示资本不变，劳动单独增加1%，产量将增加1%的3/4，即0．75%；劳动不变，资本增加1%，产量将增加1%的1/4，即0．25%。劳动和资本对总量的贡献比例为3∶1。

如果劳动和资本这两种生产要素的使用量为原来的λ倍，那么：

A（λL）α（λK）β＝λα＋βALαKβ＝λα＋βQ

显然，如果α＋β＞1，则λα＋βQ＞λQ，这时为规模报酬递增；

如果α＋β＝1，则λα＋βQ＝λQ，这时为规模报酬不变；

如果α＋β＜1，则λα＋βQ＜λQ，这时为规模报酬递减。

八、规模报酬

规模报酬（Returns　to　Scale）是探讨这样一种投入—产出的数量关系，即当各种要素同时增加或减少一定比率时，生产规模变动所引起产量的变化情况。假定一个生产面包的厂商，日产面包100万只，需要投入资本10单位，劳动为5单位，资本与劳动的比例是2∶1。如果厂商扩大生产，购买20单位资本，10单位的劳动，即各增加一倍，这时，每天生产面包的数里可能有三种情况：一是生产面包200万只；二是生产面包数超过200万只；三是不足200万只。

上述生产面包的厂商增加一倍的资本和劳动投入，产量不外乎三种情况，即：一是产量增加一倍，二是产量增加超出一倍，三是产量增加不到一倍。可见，厂商规模报酬有三种情况：

1．规模报酬递增（Increasing Returns to Scale）

这种规模报酬的特征是产出的数量变化比例大于投入的变化比例，如上例中的第二种情况。

规模报酬递增的原因有三点：

（1）生产专业化程度提高。当生产要素同时增加的时候，可以提高生产要素的专业化程度，例如，劳动者分工更细了，这会提高劳动生产效率。

（2）生产要素具有不可分的性质。有些要素必须达到一定的生产水平，才能更有效率。这表明原有生产规模中含有扩大生产的潜力。假如一个邮递员每天原来给某地段送100封信，现在有2　000封信要送时，也许只要增加2个或3个人就够了，并不需要配备20名邮递员。

（3）管理更合理。生产规模扩大时，容易实行现代化管理。现代化的管理，会造成一种新的生产力，合理的、先进的管理可以更进一步充分发挥各要素的组合功能，带来更高的效率和收益。

当一个生产经营单位规模过小时，就不能取得应有的效率，这种情况可称规模不经济。通过扩大规模，可提高效率，以取得规模经济。

2．规模报酬不变（Constant Returns to Scale）

其特征是产出的数量变化比例等于投入变化比例，如上例中的第一种情况。

规模报酬不变的原因主要是出于规模报酬递增的因素吸收完毕，某种生产组合的调整受到了技术上的限制。假定一个生产面包的工人，操纵2台机器生产面包已达到最大效率，这时要增加产量，除非是改进机器，或采用新机器，否则，这时候产量只会与投入同比例变化，使规模报酬成为常数状态。

3．规模报酬递减（Diminishing Returns to Scale）

其特征是产量的变化比例小于投入的变化比例，如上例中的第三种情况。

规模报酬递减的原因，主要是规模过大造成管理效率的下降。表现在管理上主要是内部机制难以协调，管理与指挥系统十分庞杂，一些重要问题只能一级一级反映给决策者，而重要的决定要由决策者一级一级传达给生产者，这样会贻误时机，造成规模报酬的递减。

思考与作业

1．解释生产函数概念及其基本性质。

2．1958年大跃进中曾提倡密植，结果粮食减产，解释这种现象。

3．总产量与边际产量、平均产量与边际产量之间存在什么关系？如何根据这种关系确定一种生产要素的合理投入区间？

4．在分析企业时，一年是不是一定是短期？为什么？

5．比较消费者均衡与生产者均衡的相同与不同之处。

6．等产量线的特征是什么？

7．用图形解释“脊线”概念。

8．解释柯布—道格拉斯生产函数及其实际意义。

9．设某企业有资金100万元，资本价格为每单位（例如一台机器）10万元，劳动价格每单位（每小时劳动）10元。画出该企业的等成本线。

10．企业资金增加到200万元，其他条件不变，画出新的等成本线。

11．资本价格下降为每单位5万元，其他条件不变，画出新的等成本线。

12．劳动价格上升为每单位30元，其他条件不变，画出新的等成本线。

13．已知某厂商的生产函数为，PL＝＄3，PK＝＄5，求产量Q＝10时的最低成本和使用的劳动（L）与资本（K）的数量。