(二)结构化面试试题的命制思路
1.试题命制的构思
面试试题的构思设计的好坏直接决定了整个结构化面试的成功与否。好的设计构思在一定程度上就保证了试题命制的水平和质量。要进行试题命制的构思,也就是要制定一个“试题编制计划”,就是对整个试题编制工作做通盘的总体构思,把最基本的东西先确定下来,然后在此基础上再根据需要不断使之丰富和充实,这样就保证了后面的工作有所遵循,始终围绕重点有针对性地出题。事实证明,制定好“试题编制计划”,是使编题工作按部就班、顺利完成地保证。在编制试题计划时应当明确以下内容。
(1)测评的目的:本书研究讨论的测评目的是通过面试考察候选人之间的能力差异,从而能够公开选拔出合适的党政领导人才。
(2)测评项目,也就是对哪些素质项目进行测评以及测评结果的质量要求。在选拔党政领导人才的测评中,一般主要考察的素质项目有逻辑思维能力、计划能力、决策能力、组织协调能力、人际沟通能力、创新能力、应变能力等等。
(3)测评对象,是指对应试者的总体情况要有所了解,比如说学历、专业、工作经历等,这样在编制试题的过程中才能根据个人的情况有针对性地出题。
(4)测评模式,就是选择是口试类的模式还是模拟操作类的模式。口试中是采用哪一种或哪几种,模拟操作试中是采用哪一种或哪几种,只有具体确定后,才能考虑拟题。当然本书讨论的是结构化面试,在这里应该选择口试类的模式。
(5)题型,明确采用哪些试题题型。结构化面试的题型有背景型、情景型、智力型、行为型、压力型和意愿型,在具体选用是要根据测评的目的和各种题型的应用范围选择合适的题型。
(6)取材范围,就是确定在面试过程中要选择哪些题材。前面已经讨论过在选择题材的时候可以适当注意选择一些比较新的题材,观念和形式也要注意采用一些新的东西,避免一成不变。
(7)对拟题工作的质量与数量要求。这个可以通过一些技术指标和实际的使用情况来决定。
2.试题编制的技术要求
(1)基本要求。
编制结构化面试的考试试题,首先要符合结构化面试测评的基本内容,体现结构化面试测评的基本目标。为此在编制结构化考试试题的时候要考虑到可考、可测、可评和可答等多种目标价值。
所谓可考性,就是要求试题在编题的过程中,一方面要考虑党政领导人才的共性特点,还要兼顾不同部门、职位甚至不同层次选拔领导人才的不同差异,也就是要考虑个性。只有将共性和个性相结合,才能使试题具有“可考性”,也才能使之符合职位选拔的基本条件。
所谓可测性,就是要求试题的编制是否围绕要测的重点能力展开,也就是是否抓住了重点。只有突出重点的测评试题才具有可测性。针对党政领导人才设计的面试试题,测试的重点应当放在测评应试者的实际工作能力和发展潜能上。
所谓可评性,是指通过这个试题能够拓展开应试者的素质,从而使考官能够综合的考察。在编制试题的过程中要注意尽量避免“直来直去”的问题,给考生留有发挥能力的余地。测评的试题不要太难或太易,应该是报考该职位的人员应知应会的问题,同时尽量将主观发挥性的内容与常识性的基本知识相结合,试题的范围适合考官提问和追问。
所谓可答性,是指试题的编制要考虑到应试者的情况,符合应试者的基本特点,这样有利于在考官提问的时候考生能够充分的思考和作答,而详尽和系统的回答又进一步有利于考官的追问。通过双方的充分交流和积极互动可以进一步的提高结构化面试的有效性。试题的编制既要经过行业专家学者、领导人才和组织部门的同志制定,又要经考试测评专家进行分析润色,力求内容表述准确,分量适当。
切记提问的宗旨不是将应试者“问倒”或者“难倒”,而是给应试者一个展现自我的舞台,只有等应试者将自己的所有素质都展示出来了,考官才能做出正确的评价。因此出题的宗旨是“问得好”或者“问得巧”。
除了上述提及的四个基本技术要求以外,在试题编制的过程中还有一些细节方面的要求。一是试题中所选用的语言要短小精练,清楚明确。切不可模棱两可,含含糊糊。让应试者引起理解上的错误,从而导致在答题过程中出现不必要的失误,影响应试者能力的正常发挥;二是试题本身不宜过长,太长的问题会给应试者带来理解和思维上的障碍,有些应试者往往记住了后面的问题而忘记了前提;三是试题编制过程中要注意一定的范围,不可侵犯个人的隐私,并且尽可能的回避涉及到个人隐私和应试者家庭的问题。
(2)技术规范。
①合理确定结构化面试试题的项目难度。
试题难度或项目难度就是指测验项目的难易程度。对于项目的难度和两方面的因素有关,一是要测内容本身的难易程度,另外是被试本身的知识水平和测验的编制技术。
对于那些是非题、选择题等采用二分法记分的项目,一般情况下难度都用通过率P来表示。
P值的取值范围在0—1之间,取值越大表示题目越容易,反之则难。由于本书讨论的是结构化面试,结构化面试的记分为非二分法记分,所以通常情况下难度系数可以通过下面的公式来估计:
![]()
式中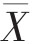 为全体被试者在某一项目上的平均分,Xmax为该项目的满分。
为全体被试者在某一项目上的平均分,Xmax为该项目的满分。
在实际操作中,当被试人数较多时要估算试题的难度通常采用分组法。所谓分组法就是将被试按照总分从高到低排列,然后将总分最高的27%的被试定为高分组,而将总分最低的27%定为低分组。分别计算两组在某个试题上的通过率,得到各自的通过率以后用下面的公式计算相应的项目难度。
![]()
式中PH、PL分别为高分组与低分组的通过率。
进行难度分析的主要目的是为了筛选项目,因此难度定在多少为合适完全取决于测验的目的、性质和试题的形式。
在实际工作中,如果只是想了解被试掌握的知识和技能等情况,这时难度取为多少并不是很重要,但一般选择接近中等难度的试题比较合适。但是对于那些选拔性的考试就应该选择那些难度值接近录取率的项目。对于公开选拔领导人才的结构化面试由于不需要考虑录取者之间的能力差异,更不需要考察未录取者之间的能力差异,所以难度系数一般定在0.5以下,整个考试试题的难度则控制在0.2左右。
②保证结构化面试试题的区分度。
区分度是指测验试题对被试者的心理特性的区分能力。可以用区分度系数D来表示。D值的范围在-1—1之间,数值越大区分度就越高。区分度越高,越容易将不同水平的被试区分开来;区分度低的试题,则不能有效区分被试的水平,水平高的和水平低的被试得分都差不多。
试题区分度系数的估计方法有三种:鉴别指数法、相关法和方差法。
鉴别指数法,即同难度系数的分组方法相同。将被试按总分高低排列,以27%的比率分成高分组和低分组,比较两组在试题通过率上的差别:
D= PH+1PL
式中PH为高分组在某试题上的通过率,PL为低分组在该试题上的通过率。二者通过率之和为鉴别指数D。
相关法,即以某一试题分数与效标分数或测验总分的相关作为该试题区分度的指标。相关系数与区分度成正比。对于结构化面试来说,一般采用两列相关法。因为测验分数是连续的,所以在计算相关系数的时候对某个试题强行规定某一分值为通过点,高为通过,低于该分值为不通过。估计相关系数的公式为:
![]()
式中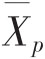 是通过的考生在整个考试中的平均分,
是通过的考生在整个考试中的平均分,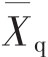 是未通过的考生在整个考试中的平均分,St是所有考生总成绩的标准差,p是通过率,q是未通过率,y是p正态曲线下对应的高度。
是未通过的考生在整个考试中的平均分,St是所有考生总成绩的标准差,p是通过率,q是未通过率,y是p正态曲线下对应的高度。
方差法,即通过计算考生某一题目得分的方差也可以作为项目区分度的指标。方差大说明数据离散程度大,考生在该项目上反应差异大,则项目的区分度就好。估计方法为:
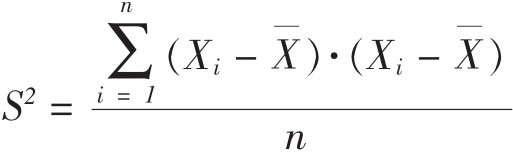
Xi是第i个考生的得分,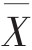 是所有考生的平均分,n是考生人数。在结构化面试中,如果考生人数太少,多是用校正的公式估计方差。校正公式为:
是所有考生的平均分,n是考生人数。在结构化面试中,如果考生人数太少,多是用校正的公式估计方差。校正公式为:
对题目区分度的评价,伊贝尔(R.L.Ebel)提出的标准如下:0.4以上为优秀,0.30~0.39为良好,0.29~0.20为勉强可用,但需要改进,0.19以下项目应淘汰或修改。如果项目区分度系数为负值,必须删除。
作为编制试题的基本要素难度,区分度是编制者在编制试题时必须要考虑的一点。在试题的编制中设置合理的难度和区分度,这就要求在设计面试试题时,与具体用人部门充分沟通,确定拟招录党政领导人才的能力、学历层次及工作经验要求,以此确定面试试题设计的难度与区分度。
③确保结构化面试试题的无偏性。
项目功能差异功能研究认为对来自不同群体的考生,测验项目应具有相同的特质。测验的偏差是指偏见或特殊的倾向。测验的有偏性是说测验对于和大多数考生有差别的那些考生或个体来说是有偏见的或不公平。如果一个项目的难度在两个不同的子群体的值有差异,则认为项目存在偏差。具有相同内在能力水平的个体,不管其所属的群体如何,在同一项目作答正确的概率相同等,该项目是无偏的,否则为偏差性。从项目反映理论来看,项目的偏差是指如果某个项目在不同的群体的项目特征曲线不同,则项目存在偏差。
检验项目差异的方法有OCI法和UCI法。OCI法有几种估计方法,回归法是其中的一种。公式为:
![]()
Y是项目分数变量,取值0—1,Z是结构化面试的总分,V是考生的分类变量。对于估计的参数β0、β1、β2、β3,如果只有β0和β1为0,说明项目无偏性,如果只有β3为0,表示该项目有均匀性偏差,如果所有的参数均不为0,表示项目有非均匀性偏差。
UCI法实际上是建立观测变量与潜变量关系的反应模型,然后比较在不同子群体数据基础上估计的项目模型是否有差异。具体步骤是:
(1)每一子群体中分别估计所有项目的参数。
(2)求所有项目两套参数之间的转换函数,利用函数实现项目参数转换。
(3)在所有项目参数转换完成后,评价项目偏差情况,删除有偏差的项目。
(4)对剩下的项目重新求取转换函数,并对所有的项目进行参数转换。
(5)再次评价所有项目的偏差情况,删除有偏项目。
(6)重复(4)、(5)两步,直到连续两次所有的项目偏差评价相同。
3.面试分数统计处理
结构化面试常用的评分方法是体操打分法。即去掉一个最高分,去掉一个最低分,取综合平均分。这种方法简便易行,便于操作。当然,在人才能力素质测评当中,常用的数理统计方法有很多,比如集中趋势分析、离中趋势分析等,这些方法在面试分数统计中也具有重要的参考使用价值。
(1)集中趋势分析。
集中趋势分析是指在大量测评数据分布中,测评数据向位点集中的情况。描述集中趋势的量数,在数理统计学中叫集中量数,其功用有二:①同是一组数据的代表值,可以用来说明一组数据全貌的一个方面的特征,即它们的典型情况;②可以用来进行组间比较,以判明一组数据与另一组数据的数值差别。在素质能力考评中,最长使用的集中趋势量数有算术平均数和中位数。
①算术平均数。算术平均数就是测量数值的总和除以测量数值的个数所得的商数,以 表示。又可分为简单算术平均数和归类算术平均数。
表示。又可分为简单算术平均数和归类算术平均数。
简单算术平均数 。
。
![]()
其中,Xi表示各个测量的数值;n表示测量的次数。
例如,某7个考生的测评结果总分分别是45,60,55,50,60,58,49,则其简单算术平均值为53.89。
归类算术平均数。
![]()
其中,f表示同一测量数值X出现的次数;n表示测量的总次数。
例如,对6个人的“言语表达能力”进行统计,其中得6分的3人,4.5分的2人,5分的1人,5.5分的3人,4分的1人,则
![]()
②中位数。中位数是全部测评数据按大小排列后的那个最中间的数值,即移居中间位置的一个点的数值——数列的集中趋势,以符号Mdn或Md表示。
n为奇数。当测量的数据n为奇数时,中位数就等于(n+1)/2项的数值。
例如:有下例9个数,依大小排列为:4、7、8、9、10、11、12、13、14(n=9)
(n+1)/2=5,序列第五的数据是10,则该组数据的中位数是10。
n为偶数。当n为偶数时,中位数就等于数列最中间两项数据相加除以2,即第n/2项的数值与第n/2+1项的数值相加的平均值。
例如:有下列8个数,依大小排列是为:2、3、5、7、8、10、15、19(n=8)序列为n/2=4者是7,序列为n/2+1=5者为8,则其中位数为(7+8)/2=7.5。
从以上举例可以看出,求中位数不受极大值与极小值的影响,而决定中位数的关键是居中的那几个数据的数值大小。
(2)离中趋势分析。
数列的离中趋势描述数列的分散程度,以差异量数来说明。一个数列只有同时用集中量数和差异量数才能体现数列的整体特征。差异量数越大,集中量数的代表性就越小;差异量数越小,则集中量数的代表性越大。
例如,有下列三组测评数据,每组7个,平均数都是10。
A:8,8,9,10,11,12,12 XA=10
B:5,6,8,10,12,14,15 XB=10
C:1,2,5,10,15,18,19 XC=10
它们的集中量数虽然相等,但它们的离散程度明显地不同。A组最集中,C组最分散,B组居中。因此,为全面反映实际测评的情况,在进行数据分析时,除必须求出集中量数以外,还需求出差异量数。在素质能力测评中,最常使用的差异量数是标准差。
标准差的计算公式为:
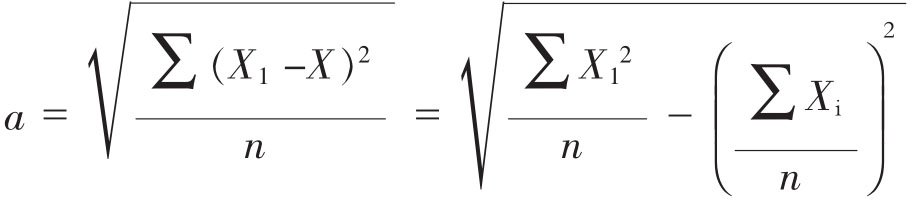
标准差是表示一组数据离散程度的最好的指标。其值越大,说明离散程度越大,其值越小说明数据比较集中,它基本具备一个良好的差异量数应具备的条件:反应灵敏;有一定的公式严密确定;容易计算;适合代数运算;受抽样变动的影响小;简单明了。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。














