对内含报酬率和修正内含报酬率的进一步讨论

3.3　对内含报酬率和修正内含报酬率的进一步讨论

【关键语】提出修正内含报酬率的初衷是为了简化报酬率的计算。修正内含报酬率是既定贴现率的函数，贴现率却不会影响内含报酬率；贴现率与内含报酬率的差异方向决定了修正内含报酬率与内含报酬率的差异方向。

从前面的阐述可以看出，计算修正内含报酬率比直接计算内含报酬率要简单得多。下面我们对修正内含报酬率与内含报酬率的关系作进一步的研究。方程（3-5）中的K是决策者事先确定的一个贴现率，MIRR是方程的未知数，一般情况下，MIRR不可能等于K。但从理论上说，至少存在这么一个贴现率K，它使方程（3-5）的解正好等于这个既定的贴现率。不难看出，这个特殊的贴现率就是前面介绍的内含报酬率（IRR）。因此，如果说修正的内含报酬率是方程（3-5）的解，那么内含报酬率就是下列方程组的解：

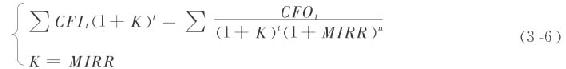
再进一步分析方程（3-5），可以看出，修正内含报酬率与既定的贴现率有关。一般地说，当预先选择的贴现率较大时，计算的修正的内含报酬率也比较大；反之亦然。如果我们将投资项目的内含报酬率看成是一个特殊的贴现率数值，那么，从方程（3-5）我们可以得出以下结论：

（1）当K＞IRR时，MIRR＞IRR，但MIRR＜K，即IRR＜MIRR＜K；

（2）当K＜IRR时，MIRR＜IRR，但MIRR＞K，即K＜MIRR＜IRR。

换言之，如果预先选择的贴现率大于投资项目的内含报酬率，那么修正内含报酬率必定大于内含报酬率，但比确定的贴现率小；如果预先选择的贴现率小于投资项目的内含报酬率，那么修正内含报酬率必定小于内含报酬率时，但比确定的贴现率大；只有当预先选择的贴现率正好等于内含报酬率时，计算的修正内含报酬率才等于既定的贴现率（此时即为内含报酬率）。

为进一步说明内含报酬率和修正内含报酬率的关系，我们通过举例说明。

【例3-3】某投资项目需第一年年初投资300万元，第二年年初投资150万元，第二年开始经营，寿命期为6年，预计第二年至第七年各年经营活动的现金净流量依次为100万元、130万元、160万元、140万元、110万元、80万元。

我们首先计算出该项目的内含报酬率（计算过程略）为IRR≈12.79%。

如果决策者的期望报酬率（贴现率）为10%，我们来计算该投资项目的修正内部报酬率。计算过程如下：

10%贴现率的现金流入量的终值为

（100×1.1⁵＋130×1.1⁴＋160×1.1³＋140×1.1²＋110×1.1＋80）

＝963.78万元

投资额的现值为436.36万元

解方程　963.78＝436.36（1＋MIRR）⁷

解得　MIRR≈11.99%

这就是前面第（2）种情形：10%＜11.99%＜12.79%，即当贴现率小于内含报酬率时，修正内含报酬率大于所取的贴现率，但小于其内含报酬率。

我们再取贴现率K＝15%，同样可以计算出该投资项目现金流入量的终值（1063.50万元）和流出量的现值（430.43万元）。解方程：430.43×（1＋MIRR）⁷＝1063.50，得MIRR＝13.79%。这就是前面第（1）种情形：12.79%＜13.79%＜15%，即当贴现率大于内含报酬率时，修正内含报酬率小于所取的贴现率，但大于其内含报酬率。