当前世界经济仍保持增长势头，但不平衡态势明显，主要经济体和地区经济发展不平衡加大。美国经济继续较快增长，日本经济稳步复苏，欧盟经济依旧低迷，亚洲地区仍为全球增长最快地区。欧元区经济明显慢于非欧元区，欧元区新老成员间经济发展不平衡也很突出。世界三大经济体虽发展不平衡，但同处新一轮经济扩张周期，目前只是增长幅度不同。当前国际贸易和跨国直接投资重趋活跃，也成为拉动世界经济较快增长的重要因素。在世界经济增长不平衡和经济复苏的大背景下，石油需求进一步扩大，国际政治、经济关系中石油筹码的分量进一步加重，使得石油问题成为各国政府关注的焦点。国际石油市场自20世纪70年代起经历了两次石油危机的打击，呈现出变化幅度大、多种复杂因素交织等特点。当前国际石油市场更是充满了动荡和不确定因素，世界石油资源的全球分配形势更趋复杂，因此深入研究未来世界石油生产消费形势的变化对世界经济的稳定和发展具有重要意义。要把握世界石油生产和消费的形势，有必要基于历史数据对未来5～10年石油形势进行预测，这里要说明的是预测只是对于趋势的分析和判断，况且在预测的基础上各国进行不同程度的宏观调控，并不能认为预测的结果未来一定会发生。
西方学者对国际石油市场的关注由来已久，以Campbell、Deffeyes和Laherrere等为代表的一些欧洲地质学家专门成立了研究世界石油天然气产量的ASPO组织（ASPO-The Association for the Study of Peak Oil and Gas）。研究中发现世界石油生产的增长并不会保持持续增长的态势，这是因为世界石油资源的有限且不可再生的，石油产量在未来会达到顶峰。
一般资料常用“储采比”即“已探明石油储量”与“当年石油产量的比值”，来表征尚可开采的年数。该系数假定储量和年产量均保持不变，实际中随着勘探生产技术变化，储量和年产量均是不确定的，作为不可再生资源的石油，其生产增长幅度（边际产量）会逐渐减小，故用储采比反映未来生产形势有局限性。
美国地质学家M．King Hubbert（1956）根据油井生产周期提出著名的“哈伯特倒钟理论”，即石油产量可以持续增长至累计产量达到总储量的一半，之后产量增加潜力减弱，生产进入平台期或转而下降期。哈伯特基于此理论于1956年准确预测出美国48个州石油产量1970年到达顶峰，英国等世界上多例生产历史数据也很好地支持这一理论（ASPO网站）。
经典哈伯特模型采用LOGISTIC回归，根据某一设定的最终储量给出平滑、理想的倒钟形生产曲线，中心点即为产量见顶的时间点。实际中，由于资金投入、勘探生产技术条件变化，最终储量并非某一确定值，而是一个不确定的随机变量。另外，产量由于受市场价格、政治干预、自然条件变化等影响，用单一的光滑钟形曲线不能很好地拟合全部历史生产数据。
Colin Campbell（2002, 2003）基于“哈伯特理论”，考虑各个世界主要石油生产国家近5年平均生产增长速度，未来产量按照线性递推，累加各国产量即为世界产量，当累积产量达到设定的最终储量一半，即为产量见峰时间。由于石油勘探要提前于生产进行，Laherrere（2001, 2002, 2003, 2005）基于勘探和生产历史数据，认为生产曲线是勘探曲线的某一时间平移，存在周期，从而根据现存石油勘探情况评估未来生产的态势。Kenneth．S．Deffeyes（2001）利用经典哈伯特理论分析世界石油产量的前景，结论是全球原油产量现在正处于达到顶峰的前夕。
我们根据简单、实用和有效的原则，构建世界石油生产模型。考虑到世界石油勘探发现高峰在60年代，在此之后石油勘探发现一直不景气，故我们构建的世界石油生产模型以1970年作为起点。在1973年石油危机之前，世界石油产量足以满足当时的消费量，而且由于开采成本较低，因此消费增长一直保持较为平稳的态势，我们构建的世界石油消费模型选择1965年作为起点能够较好地体现石油消费的连续性。由于1978年是中国改革开放的新起点，中国经济以及石油生产和消费面临的是体制转型和结构调整的新变化，从第一节突变点的计算中也验证这一点，况且在此之前中国石油消费的数量不大且数据不完整，所以我们选取1978年作为构建中国石油生产和消费预测模型的起点。
现代时间序列分析表明，世界石油生产与消费年度数据是具有单位根性质的非平稳过程，虽然可以通过差分平稳化，但却会带来数据信息损失。此外，由于石油生产与消费本身具有一定的继承连贯性，而且其样本量不大，采用人工神经网络等方法则可能会产生过度拟合等问题，经综合考虑选用了Holt双指数平滑方法。
Holt双指数平滑方法兼容了全期平均和移动平均所长，不舍弃过去的数据，但是给予逐渐减弱的影响程度，即随着数据的远离，赋予逐渐收敛为零的权数。单指数平滑预测值乃是序列按衰减系数（平滑系数）递推，平滑的结果有滞后实际的不足。王冬星（2005）指出，双指数平滑可以弥补缩小预测对于实际值的滞后，可以反映长期性趋势和周期性趋势。而且，双指数平滑预测具有“学习记忆”的特点，可根据历史数据，不断提高预测精度。Holt双指数平滑与Brown双指数平滑的区别在于，当单指数平滑方程第二次被应用的时候，Holt的方法允许使用不同的平滑常数（β），而Brown方法则在两次使用中都是一常数。
下面建立世界石油产量和消费的预测模型。
单指数平滑
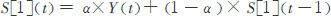
Holt双指数平滑
其中S［2］（t）代表双指数平滑在t时刻世界石油产量或消费的“平滑估计”，S［1］（t）代表单指数平滑在t时刻世界石油产量或消费的“平滑估计”，Y（t）是t时刻产量或消费的历史数据值，α和β是数值介于0和1之间的平滑常数，取值根据RMSE取最小值时确定。
计算中用到的统计量为：
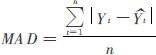
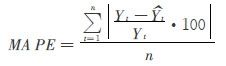
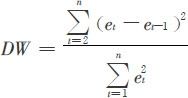
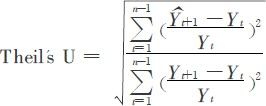
其中Yt是t时刻的实际值，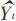
是t时刻的预测值，
。
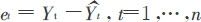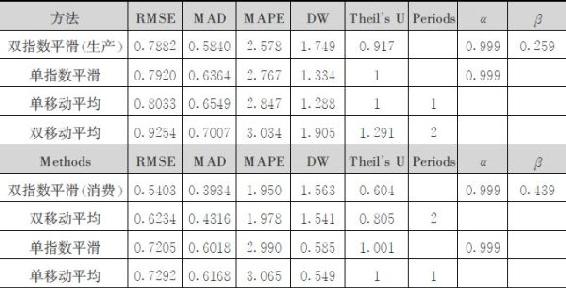
根据《BP能源统计报告2005》的1970—2004年世界石油生产数据和1965—2004年消费数据，对于世界石油生产（1970—2004）和世界石油消费（1965—2004），采用不同预测方法拟合结果如下。对比结果可看出Holt双指数平滑方法较单指数平滑和移动平均方法效果要好。利用双指数平滑方法构建的模型有较小的拟合误差和模型系统风险，有较高的精度，较好地处理了序列相关性问题，实际拟合效果较好。
预测世界石油生产中的参数α＝0.999，β＝0.259是根据RMSE取最小值（0.7882）而得到的。
预测世界石油消费中的参数α＝0.999，β＝0.439是根据RMSE取最小值（0.5403）而得到的。
表2-3 对世界石油生产和消费进行双指数平滑预测的参数表
由于石油资源的有限性，根据地质学的研究，石油产量不可能无限期地持续上升。笔者根据《BP能源统计报告2005》的1970—2004年世界石油生产数据和1965—2004年消费数据，以及美国地质调查局报告《USGS2000》提供的有关数据，基于“哈伯特理论”，采用蒙特卡罗模拟与双指数平滑预测方法，构建世界石油产量峰年模型。
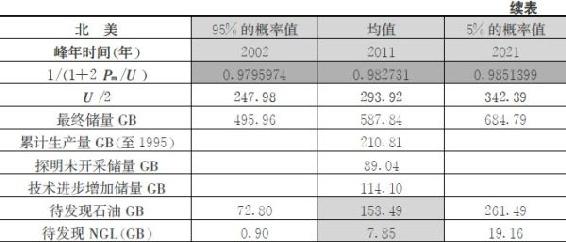
构建世界石油产量峰年模型的关键是要估算出石油最终储量U。
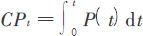
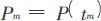
U为最终储量，Pm为峰年时的产量
U1为累计生产量
U2为探明未开采储量
U3为技术进步增加储量
U4为待发现储量（包括两部分：U41为待发现原油产量，U42为待发现液化天然气产量）
累计生产量U1来源于美国地质调查局报告《USGS2000》数据（截至1995年），探明未开采储量U2数据来源于《BP能源统计报告2005》。石油最终储量U中技术进步增加储量U3和待发现储量U4具有不确定性，《USGS2000》通过专业评估给出其三角概率分布，即95％和5％水平下可能出现的数值以及分布的均值（见表2-4）。《USGS2000》给出世界范围内技术进步增加储量的三角分布为：在95％的概率水平上为2050亿桶，均值7296亿桶，在最大5％的概率水平上为11020亿桶。
表2-4 有关产量峰年的原始数据和计算结果
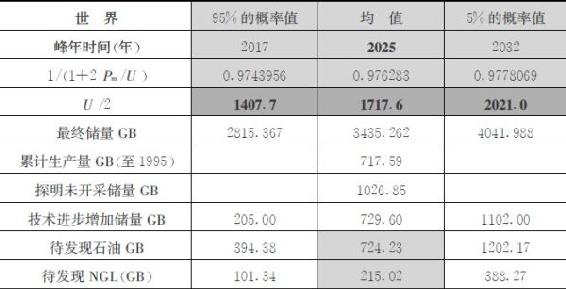
注：1GB＝10亿桶
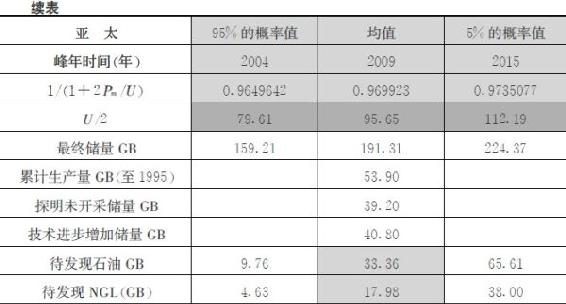
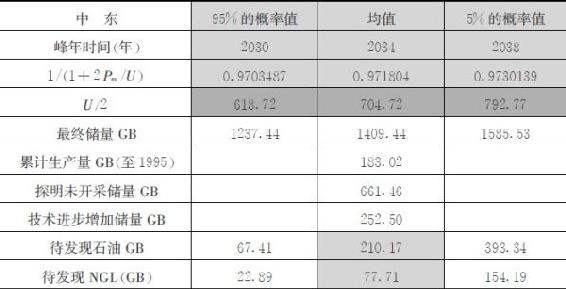
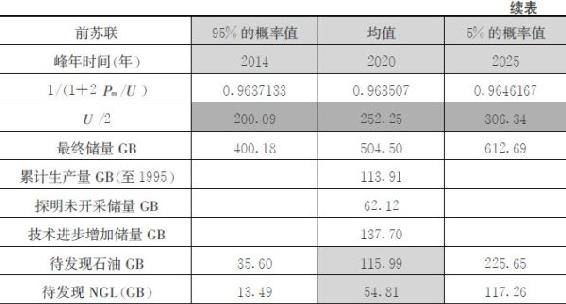
注：为保持数据来源的一致性，仍使用前苏联
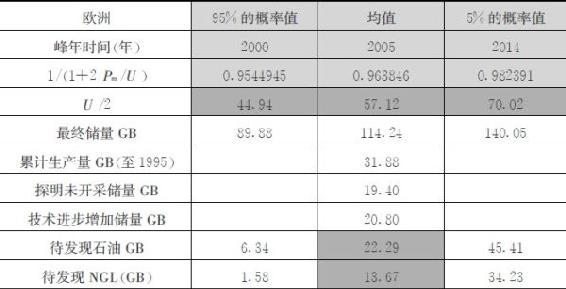
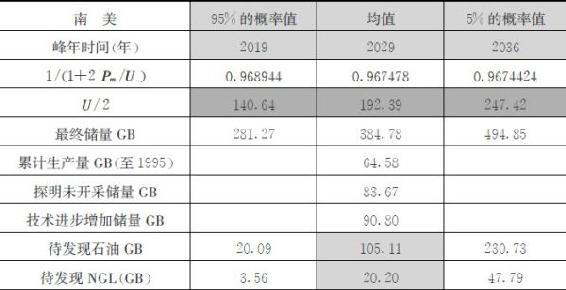
我们应用随机模拟和分层抽样技术对石油最终储量进行估计。随机模拟通过大量统计抽样实现，不受状态维数、变量分布、函数是否非线性等限制。如果某一风险变量X的期望μ和方差σ2均存在，且σ≠0（否则X就不是风险变量），蒙特卡罗模拟的误差为：
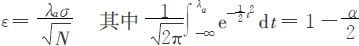
λα为正态差；α为显著性水平；N为样本数；σ为标准差。
分层抽样（Stratified Sampling）是现今最有效的方差缩减技术。Minkkinen（2004）总结出分层抽样的基本思想：通过抽样区间划分，避免传统抽样多集中发生概率较大处，使抽样遍布全空间（参见图2-3），克服变量分布畸形影响，加速模拟收敛，显著提高模拟精度与效率。
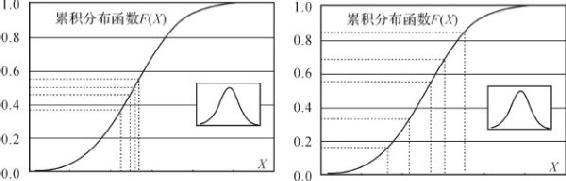
图2-3 正态分布5次传统随机抽样与分层抽样在累积分布图中的对比示意
从另一角度考察分层抽样对模拟结果影响。设定义［0, 1］上函数f（x）的积分为I，将［0, 1］划分为k个子区间：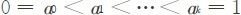
，第j个区间抽样数nj，则I无偏估计量及方差为：
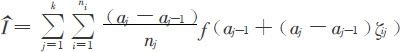
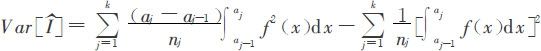
可见，适当选择分点a1，…，ak－1及nj可使方差显著降低。对定义在［a,b］上函数g（t）则可通过积分限变换化为定义在［0, 1］上函数f（x）。
模拟随机数生成器采用数学包IMSL中程序（Multiplicative Congruential Generator），生成的随机数具有长周期（231－2＝2,147,483,646）等优良性能。Tasos C．Christofides（2005）指出，根据逆变换定理，设随机变量X概率分布函数F，对产生［0, 1］上均匀分布随机数R作F－1（R）变换即得服从分布F的随机数。
笔者将模拟次数增加到5000次，由于同时采取了分层抽样模拟策略，大大提高了随机模拟的精确度。
世界石油产量峰年之后，产量变化的趋势如何？通过大量单个油井产量变化的统计数据显示，油井产量见峰之后其产量与累计产量存在类似线性逐渐递减的关系（参见图2-4）。本书基于以上统计结果，对产量见峰之后变化的情况进行如下数学推导：
图2-4 石油产量由高峰逐步下降的变化示意
这里CPt代表t时刻累计生产量，Pt代表t时刻产量，U代表最终储量。通过（U，0）和
两点的直线：
又
故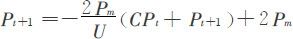
展开得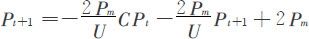
将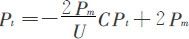
代入上式替换CPt
故可得
由此可见，石油产量峰年之后，产量之间的变化以指数形式递减，但伴随着最终储量U的变化，产量递减的速度也会有所不同。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
