【摘要】:7.4.2 复杂度偏离效应VAR模型的识别与检验数据的稳定性检验按照ADF检验,可知ln为平稳序列,而ln1也是平稳序列,CSD为一阶单整序列,即CSD1为平稳序列,因而可以针对两者的一阶单整序列展开VAR实证分析。图7.14 复杂度偏离VAR实证的AR根图采用滞后2阶的VAR模型后,获得AR根的图。
7.4.2 复杂度偏离效应VAR模型的识别与检验
(1)数据的稳定性检验
按照ADF检验,可知ln(REER)为平稳序列,而ln(REER)1也是平稳序列,CSD为一阶单整序列,即CSD1为平稳序列,因而可以针对两者的一阶单整序列展开VAR实证分析。
表7.5 复杂度偏离VAR实证的单位根检验

(2)VAR模型滞后结构检验
按照Nerlove(1990)简单法则,即22个样本,判断采用滞后2阶的VAR模型。获得2阶滞后模型的AR特征多项式图。
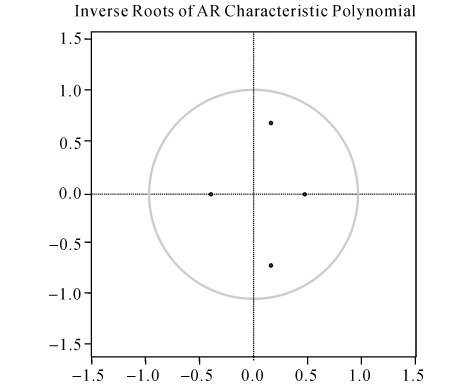
图7.14 复杂度偏离VAR实证的AR根图
采用滞后2阶的VAR模型后,获得AR根的图(图7.14)。可以看到模型的所有单位根的模的倒数小于1,即位于单位圆内,模型是稳定的。
(3)VAR模型序列相关检验
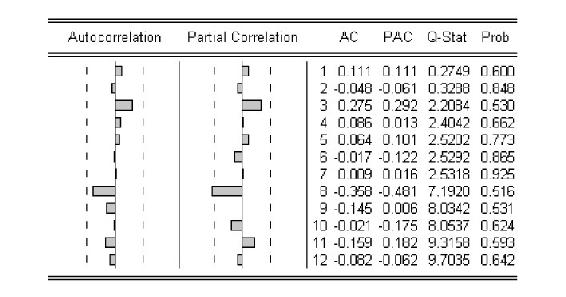
图7.15 复杂度偏离VAR模型的相关图和偏相关图
在完成VAR回归后,提取残差序列,得到回归残差相关图与偏相关图(图7.15),确定回归模型的序列相关形式是否应包括AR项或MA项,针对VAR回归序列的残差进行的相关图检验结果显示,不存在序列相关。
(4)Granger因果检验
表7.6 复杂度偏离效应实证的Granger因果检验

表7.6结果显示,我国的实际汇率变动是我国的贸易复杂度偏离的Granger原因,而我国的贸易复杂度偏离不是我国实际汇率变动的Granger原因。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















