渐进式延迟退休方案及其实施步骤

目前，延迟退休年龄的改革已成定局，渐进式推进在学界也已基本形成共识。但在何时开始、如何“渐进”上还存在差异。中国社会科学研究院的高庆波博士等主张女干部到2030年、女职工到2050年60岁退休。^[1]中国社科院的林宝博士在中国党政干部论坛上建议从2015年开始至2045年，用30年时间逐渐把男女退休年龄统一提高到65岁。^[2]辽宁大学的穆怀中和柳瑞清教授、中国人民大学的郑功成教授也分别提出了从2015年左右开始的三个方案。^[3]

本研究设计的渐进式延迟退休年龄的目标为：从2018年开始，用20年时间、分两阶段逐步实施，至2038年实现男女均65岁退休。

一、采用渐进式延迟退休年龄的必要性

延迟退休年龄的争议的实质是利益相关者的利益纷争，其阻力主要来自原双轨制的养老保险制度与社会惯性。2015年1月14日，国务院发布的《关于机关事业单位工作人员养老保险制度改革的决定》，明确了机关、事业单位建立与企业相同基本养老保险制度，实行单位和个人缴费，改革退休费计发办法。国务院的这项决定是方向性的，其基本原则是公平与效率相结合、权利与义务相对应、保障水平与经济发展水平相适应、改革前与改革后待遇水平相衔接、解决突出矛盾与保证可持续发展相促进。该决定减小了由原双轨制的养老保险制度带来的利益相关者的矛盾冲突。

一个稳定的社会形态，总是由它内部的矛盾着的诸方面的力量对比来确定的。矛盾的主要方面和非主要方面在发展过程中的变化，是新旧事物替代的表现。社会惯性的存在对社会的发展有巨大的影响，必定对变革产生阻力。任何社会变革、改良都是社会利益的重分配，必然引起新的利益分化，“改革机关事业单位工作人员养老保险制度，直接关系广大机关事业单位工作人员的切身利益，是一项涉及面广、政策性强的工作”。虽然国务院要求“各地区、各部门要按照本决定制定具体的实施意见和办法，报人力资源社会保障部、财政部备案后实施”，“省级统一集中管理数据资源，实现规范化、信息化和专业化管理”，但是完成此项改革，社会公众要有一个适应过程。到目前为止全国相继实行了机关事业单位工作人员养老保险制度改革，但并轨后的善后事宜还在研究、落实之中。延迟退休年龄这一举措当然是一种更大的社会变革，也必然引起利益相关方不同的反响。在利益整合趋向不明时，或被普遍认为这种变革最大获益方将是国家时，社会惯性是必然的表现。绝大部分民众选择按现行政策退休也是很正常的选择。在笔者进行的民意调查中，还有19.8%被测者选择延长1～2年退休，这也是近五分之一的较大选项。应该说这也是近年来关于延迟退休的讨论与政府有关这方面的宣传、说明的潜移默化作用的结果。既然是大势所趋，宁可主动选择最小的变革。

因此，养老保险制度的并轨与完善需要时日，克服社会惯性更需时日。在延迟退休年龄制度改革问题上，面对争论和分歧，政府决策既不能无所适从、错失良机，也能操之过急、企图一蹴而就。2018年仍是我国劳动人口的高峰期，此后将逐步下降。从2018年开始，用20年时间、分两阶段逐步实施，至2038年实现男女均65岁退休，大致与我国老龄化进程一致。采用渐进式延迟退休年龄的方式是整合社会利益、克服社会惯性，保证退休养老制度改革顺利推进的必然选择。

二、辅之有条件弹性退休制度

世界上不少国家都有弹性退休的规定，前述OECD主要国家在弹性退休制度上的许多做法也给我们带来了启示。国务院1978年6月颁发的《关于工人退休、退职的暂行办法》和《关于安置老弱病残干部的暂行办法》（国发〔1978〕104号）也规定符合有关条件的可以办理提前退休。国务院1993年颁布《国家公务员暂行条例》也颁发了提前退休的规定。因此，实行弹性退休制度既是世界各国的通行做法，也是我国长期社会退休养老保障工作的经验积累。本方案设计在现行国家规定的退休年龄（女工50岁、女干部55岁、男60岁）到65岁之间实行有条件弹性退休。工作条件艰苦的劳动者、体弱多病者、其他特殊情况者可提前退休。实行弹性退休的不得再从事其他有收入劳动。弹性退休者获得的退休金按其对社会的累积贡献大小与正常退休者有区别。

三、渐进式和柔性延迟退休方案

（一）渐进式延迟退休

本方案设计从2018开始。第一阶段从2018年至2028年，女工人每年延迟1岁、女干部每年延迟0.5岁，花10年时间至2028年前，女工人与女干部同步达到60岁退休。第二阶段从2028年开始，男女均每1年延迟0.5岁退休，再花10年时间至2038年实现男女65岁同龄退休。

（二）柔性延迟退休

本方案在渐进式延迟退休年龄基础上，提出的弹性（柔性）退休制度。未达到或超过法定退休年龄的、符合有关条件的可弹性退休（提前或延迟）。

（1）年满55周岁，连续的工龄或工作年限满15年且符合国务院1978年6月颁发的《关于工人退休、退职的暂行办法》和《关于安置老弱病残干部的暂行办法》（国发〔1978〕104号）规定从事井下、高空、高温、繁重体力劳动和其他有害健康工种的职工，或经医院证明，并经劳动鉴定委员会确认，完全丧失劳动能力的职工，可实行弹性退休；或国家规定工作在高原地区，电、磁射线辐射等岗位按规定折算后的工龄、年龄达到法定退休年龄的可实行弹性退休。设计依据：一是国务院1978年6月颁发的《关于工人退休、退职的暂行办法》和《关于安置老弱病残干部的暂行办法》，这两个办法经三十多年的实践，证明是必要与可行的，既从人文关怀出发，保护了特殊工种的职工与老弱病残群体，又情理兼备，恰当地体现了社会保障的相对公平；二是兼顾渐进式延迟退休的目标年龄。

（2）年满60周岁，且工作年限满30年的公务员可实行弹性退休。设计依据：一是《国家公务员暂行条例》；二是兼顾渐进式延迟退休方案中的男女65岁同龄退休目标。

（3）达到法定退休年龄，身体健康，本人与雇主均同意继续工作的可实行弹性退休。

（4）实行弹性退休的人员不得再从事其他有收入劳动。

（5）实行弹性退休不仅要有条件限制，且养老金的领取也应该参照OECD国家的做法实行区别对待，达60岁，弹性退休者才可领取一定比例养老金。比如美国规定最早62岁退休时可领取70%的法定养老金，此后每推迟一个月退休，养老金按比例上涨。西班牙的退休年龄制度规定：工人于60至65岁退休，每早一年退休其养老金收入要降低8%。德国则规定提前退休领取了部分养老金并取得其他收入的仍需缴纳养老保险费。这些都可作为我国政府制定弹性退休有关实施细则的重要参考，使弹性退休制度符合我国的实际情况，达到既鼓励有条件的劳动者延迟退休，又有效抑制提前退休的目的。具体的实施细则有待国家确定延迟退休方案，政府职能部门测算后确定。本方案未予设计。

四、渐进式延迟退休年龄方案的宏观经济效应分析

对于本方案的可行性，这里主要从其宏观经济效应角度进行分析。

（一）关于劳动力的增加

按照上一目设计的延迟退休方案，不仅涉及相关者的退休时间、养老保险待遇，而且还会引起社会从业人员量的变化。

1.从业数量的增加与累计方式

以女干部为例，设某年达到g0=55岁的女干部有q人，新方案规定该年的退休年龄为g1岁（g1﹥g0），则与原退休方案比较，她们将多提供q（g1-g0）的从业数量，从业量的计量单位是：人·年。这与工厂中用“已使用台时数”计算设备的使用数量是同一个道理。1个人工作5年，从业数量为5；10个人工作半年，从业数量也是5。这里提出从业数量的概念，是为了与劳动力数量相区别，以避免歧义。

为便于数学处理，用i表示年序，i=0表示2017年，i=1表示2018年，以此类推。

第i年（1≤i≤20）新方案规定的退休年龄为gi=g0＋0.5i（每1年延迟0.5岁），设qi为第i年达到周岁的人员数量，简称到龄人数，则该年（按前置方式确定）发生的新增从业数量fi=qi（gi-g0）=0.5iqi，从业数量fi将存续0.5i年，即延续到第i＋0.5i=1.5i年。

从第1年（2018年）到第n年（≤20），从业数量的增加总量等于所有满足i﹤n的fi累积，但不能全额累计，超出n年的部分应予扣除。当1.5i≤n时，fi全额参加累计；当1.5i﹥n时，总0.5i共的存续时间，有1.5i-n在第n年之外，有n-i在第n年之内，按比例折算，参加累计的数量应为根据上述分析，计算这n年中从业数量的增加总量Qi，需分段累计为

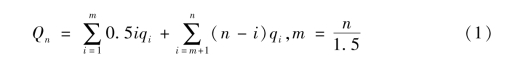
需要说明的是，就全国宏观而言，达到55周岁以及延迟退休的情况每天都在大量发生，因而实际变动可视作处于连续状态，在建立数学模型时，不必拘泥于个别微小局部的不规则跳动。比如（1）式中的可能不是整数，作为求和序号似乎不妥，其实不然。面对连续状态，累计的本质是积分，求和则相当于分段积分，出现非整数并不为怪。

2.回归分析的作用

公式（1）用于实际计算还存在两个问题：一是到龄人数qi逐年不同，公式无法简化，因而计算不便，并且难以开展后续分析；二是qi为预测数，预测的准确性会在很大程度上影响公式的效用。

为此，需对公式（1）做改进。下面用回归分析方法对qi作进一步的研究。简单的一元线性回归是根据已知数据（xi，yi）（i=1，2，L，n），用最小二乘法建立回归方程y=＋x，其中的，称为回归系数，计算公式为：

这里的δ称为比例回归系数。系数δ的测算可利用相关文献的数据。^[4]，有若干组关于2010—2050年劳动力供给的预测数据，取其中2018—2050年44-65岁的一段数据yi（i=1，2…33），可按上述公式算得δ=-0.00621。上述公式中的yi与（1）式中的qi性质相同，都是我国同一时段同一年龄段的劳动力供给预测，所以它们的比例回归系数应该相近。现将上述回归方程中的x，y分别换成i和q，得到

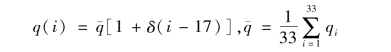
其中：17是i=1，2…33的平均值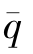，是改革过渡阶段的年平均到龄（55岁）人数，q（i）表示qi的回归估计。用q（i）代替（1）式中的qi，可得

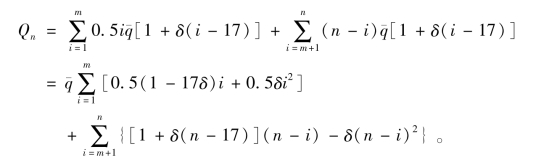
自然数求和有现成的数学公式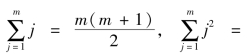：此公式具有内插和外推功能，当m为非整数时也能适用。将这些公式用于上面Qn的求和，可化简整理为

3.女干部劳动力的增加量

女干部是简称，包括所有按原退休方案到55岁退休的女性从业人员。

计算（2）式的差分：

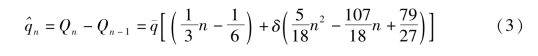
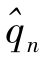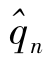表示n年的累计量减去前n-1年的累计量，显然等于第n年的从业数量的增加量，这相当于个人工作一年（第n年）的从业量，所以就是第n年因按新方案实施延迟退休所增加的（女干部）劳动力数量。

公式（3）的优点首先是计算简便，只要将δ，n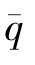，三个数据代入即可；其次是预测数据只需用到年平均到龄人数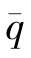，不必细究逐年的到龄人员，相对而言，预测准确度的把握要容易得多；最后，到龄人员的变动系数δ可适当调节，若依据更详尽的资料测算δ，则可进一步提高公式的精度。

公式（3）还可变形为

其中的bn即（3）式中的方括号，δn为方括号内两项的比值。bn反映第n年内劳动力增量与年平均到龄人数的比例，称为倍率系数；δn相当于令δ=0时计算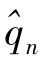引起偏差而需加以补偿的比例，称为粗算偏差率。

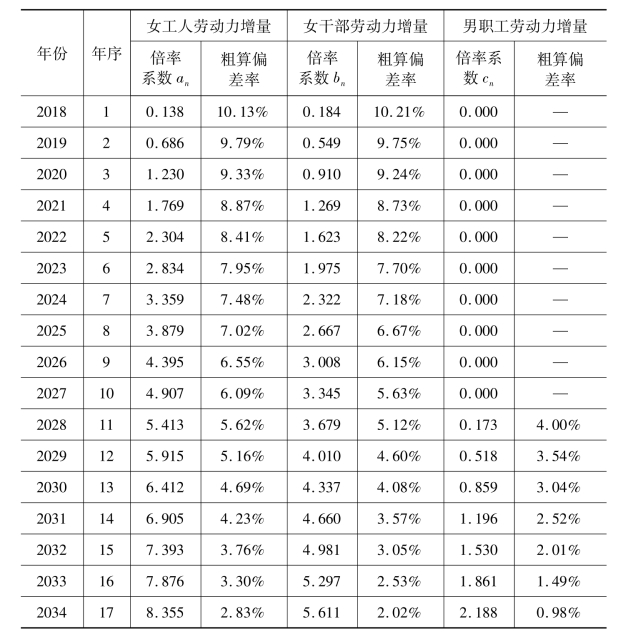
将已经测算得到的δ=-0.00621代入（3），可算得倍率系数bn和粗算偏差率δn，如表11-1所示：

表11-1　女干部劳动力增加量的倍率系数和粗算偏差率

续表

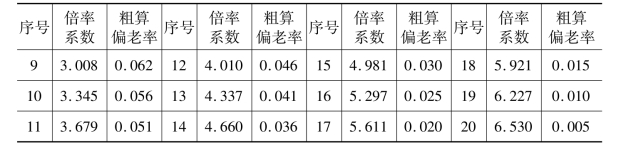
计算结果表明，随着到龄人数的积累，倍率系数同步增长，偏差率逐年走低。在前10年的计算中偏差率为5.6%～10.2%，说明虽然比例回归系数δ很小，但将其忽略不计会引起较大偏差。

公式（3）给出了实施延迟退休方案过渡时期前两个阶段每年的劳动力增加量。依据同样的思路，可计算第三阶段第n年（21≤n≤33）女干部劳动力的增加量。仍然先累计从业数量，不仅要累计第三阶段的增加量，还要累计前两个阶段的增加量。

第三阶段的第i年（21≤i≤33）延迟退休10年（65岁退休），则该年发生新增从业数量为f1=10qi，fi将存续10年，即持续到第i＋10年。

当n≤29时，前两个阶段（1≤i≤20）最迟将延续到第30年，超过第n年，故需以1.5i=n为界分两段累计，第三阶段（21≤i≤33）因i＋10﹥n（全超过）不需分段累计。所以第1年到第n年从业数量的增加总量分三段计算：

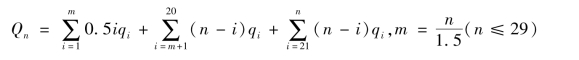
显然这个表达式与（1）一致，因而差分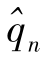=Qnn-1与（3）相同，即（3）式适用于1≤n≤29。

当30≤n≤33时，前两个阶段（1≤i≤20）因1.5i≤n不需分段累计，其累计值与n无关，在计算差分时不起作用，故只需累计第三阶段。第三阶段需以i＋10=n为界分两段累计，所以

其化简方式与前面相同，以q（i）=[1＋δ（i-17）]代替qi，化简后可得

于是

第30年的增加量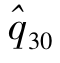用插值法估算，可保持平滑性。具体做法是分别由（3）和（4）式，得

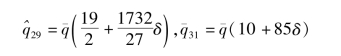
取中间的插值作为的估算值，即

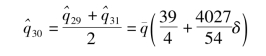
4.男职工劳动力的增加量

男职工是指所有按原退休方案到60岁退休的男性从业人员。在实施延迟退休新方案的第n年，因延迟退休而增加的男职工劳动力数量记为。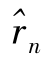

当n≤10时，显然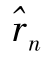=0。当11≤n≤20时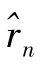，的计算方法与女干部的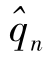基本相同，只是改革推迟了10年。下面列出简要的分析过程。

新方案规定第i年（11≤i≤20）延迟退休0.5（i-10）年（每1年延迟0.5岁），设ri为第i年的到龄（60岁）人数，则该年发生新增从业数量为fi=0.5（i-10）ri，fi将存续0.5（i-10）年，即持续到第i＋0.5（i-10）=1.5i-5年。

从第11年到第n年（11≤n≤20），从业数量的累计从i=11起需分1.5i-5≤n和1.5i-5﹥n两段累计，因而在这n-10年中从业数量的增加总量为

表达式（5）与（1）很相似，故可重复相同的化简过程，得到与（2）类似的结果：

由此可得第n年（11≤n≤20）男职工劳动力的增加量为

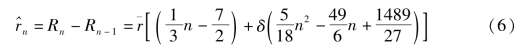
其中的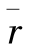表示改革过渡阶段男职工的年平均到龄（60岁）人数。

由于Rn的累计阶段离过渡阶段的中心i=17比较近，δ的累积作用不明显，所以在（6）式中取δ=0予以忽略，产生的粗算偏差率较小，在0.6%～4.0%之间。

同样考虑第三阶段男职工劳动力的增加量。第三阶段的第i年（21≤i≤33）延迟退休5年（65岁退休），则该年发生新增从业数量fi=5ri，fi将存续5年，即延续到第n年。

当n≤24时，第二阶段（11≤i≤20）发生的新增从业量，最迟将延续到第25年，超过第n年，故需以1.5i-5=n为界分两段累计，第三阶段（21≤i≤33）因i＋5﹥n（全超过）不需分段累计，所以第11年到第n年从业数量的增加总量分三段计算为

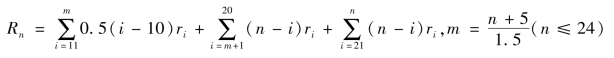
显然这个表达式与（5）一致，因而差分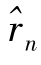=Rnn-1与（6）相同，即（6）式适用于11≤n≤24。

当25≤n≤33时，第二阶段（11≤i≤20）因1.5i-5≤n不需分段累计，其累计值与n无关，在计算差分时不起作用，故只需累计第三阶段。第三阶段需以i＋5=n为界分两段累计，即

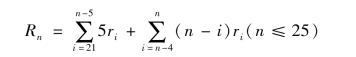
其化简方式与前面相同，以r（i）=[1＋δ（i-17）]代替ri，化简后再求差分可得第n年男职工劳动力的增加量为

然后用插值法估算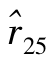，得到

5.女工人劳动力的增加量

女工人是指所有按原退休方案到50岁退休的女性从业人员。在实施延迟退休新方案的第n年，因延迟退休而增加的女工人劳动力数量记为。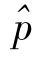

因为女工人的延迟退休方案分两个阶段实施，所以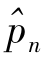的计算要复杂一些，但基本方法相同，下面列出简要的分析过程。

先考虑第一阶段。新方案规定第i年（1≤i≤10）延迟退休i-0.5年或i年（每半年延迟0.5岁），平均延迟i-0.25年，设pi为第i年的到龄（50岁）人数，则该年发生新增从业数量fi=（i-0.25）pi，fi将存续i-0.25年，即持续到第2i-0.25年。

从第1年到第n年（n≤10），从业数量的累计需分2i-0.25≤n和2i-0.25﹥n两段累计，因而在这n年中从业数量的增加总量为

以回归方程p（i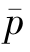）=-[1＋δ（i-17）]代替上式中的pi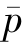，表示改革过渡阶段女工人的年平均到龄（50岁）人数，则和式（7）可化简为

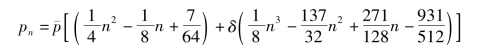
由此可得第n年（1≤n≤10）女工人劳动力的增加量为

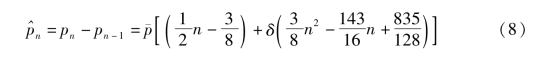
再考虑第二阶段。新方案规定第（11≤i≤20）年延迟退休10＋0.5（i-10）=0.5i＋5年，故该年发生新增从业数量为fi=（0.5i＋5）pi，fi将存续0.5i＋5年，即持续到第1.5i＋5年。计算第1年到第n年（11≤n≤20）从业数量的增加总量时，不仅要累计第二阶段的增加量，还要累计第一阶段的增加量。

当n≤19时，第一阶段（1≤i≤10）发生的新增从业量，最迟将延续到第19.25年，超过第n年，故需以2i-0.25=n为界分两段累计，第二阶段（i≥11）因1.5i＋5﹥n（全超过）不需分段累计。所以第11年到第n年从业数量的增加总量分三段计算为：

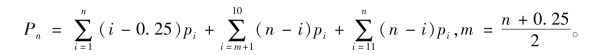
此式与（7）相同，因而差分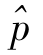=Pnn-1与（8）相同，即（8）式适用于1≤n≤19。

接下来考虑第三阶段第n年女工人劳动力的增加量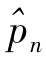。第一阶段增加的从业量都延续到第20年前，故不必参加累计。第二阶段（11≤i≤20）增加的从业量最早延续到第21.5年，最迟延续到第35年，所以当22≤n≤33时需以1.5i＋5=n（11≤i≤20）为界分两段累计。第三阶段第（21≤i≤33）延迟退休15年（65岁退休），该年发生新增从业数量为fi=15pi，并且都延续到第33年以后，故不需分段累计。根据这些分析，计算第11年到第n年从业数量的增加总量为

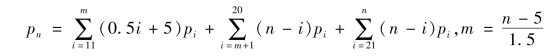
化简方法与前面相同，化简结果为

于是第n年女工人劳动力的增加量为

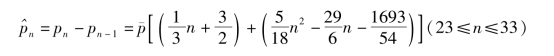
对于20≤n≤22，仍用插值法估算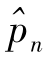，先由上面的公式算得

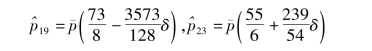
然后用插值法估算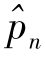（20≤n≤22），得到

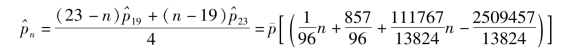
6.平均到龄人数的预测

以上的计算公式中涉及的年平均到龄人数都是预测数据，可依据有关的文献资料测算。例如由44—65岁的劳动力供给量的逐年预测数据yi（i=1，2，L，33），可算出年平均数y-。因为44—65岁含有22个年龄，不妨假定平均分布，则50岁、55岁、60岁的劳动力年平均供给量均为。在劳动力的构成中，女工人、女干部、男职工的比例在相对不太长的时段内会保持稳定，可通过适当的数据资料确定这三类人员所占的百分比，设为α，β，γ（α＋β＋γ=1），则女工人、女干部和男职工的平均到龄数量可分别预测为

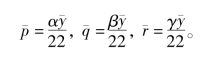
前面给出的第r年劳动力的增加量的计算公式都有相同结构：

其中的an，bn，cn为相应的倍率系数，其计算公式归纳如下：

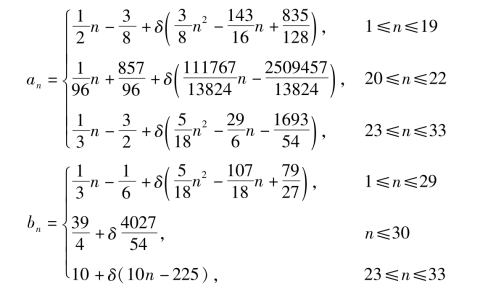
其中δ是比例回归系数，参考值δ=0.00621。按此参考值计算各倍率系数及其粗算偏差率之值，如表11-2所示。按新方案实施延迟退休，第n年因此增加的劳动力总量为

表11-2　劳动力逐年增量的倍率系数及其粗算偏差率

续表

考虑到延迟退休，本文采用二维指标：从业数量=人数×年，某一年（第n年）的新增从业数量Sn=pn（女工人）＋qn（女干部）＋rn（男职工）。

因为这些均为预测数据，考虑到尽量减小偏差因素的影响，经推导，认为采用当年新增从业数量=倍率系数×预测平均值，主要观测指标是倍率系数，从表11-2计算数据可见，倍率系数逐年递增，结论支持在新的延退方案实施后，从业数量增加。

虽然目前国家大力推进产业升级转型、科技成果产业化，减少劳动密集型产业，但就中国国情来讲，这依然需要一个相当漫长的时期。同时，计划生育等因素影响，造成人口老龄化、劳动力不足，“用工荒”现象已逐渐显现，今后若干年这一趋势还将不断显著。延退方案实施后，从业数量的增加，恰好可以缓解社会劳动力的不足。

南京财经大学沈飞对我国2010年人口普查数据，综合运用Brass生命表模型和劳动参与率模型，以3个方案对未来40年中国劳动力的供给进行了预测，均得出了人口老龄化将引发劳动力供给大幅下降的结论，3个方案的预测数据基本一致。我国劳动力数量将从2014年7.8亿的峰值开始持续下降，到2050年降至6.3亿，降幅为1.5亿，年均下降率接近（见图11-1）。^[5]

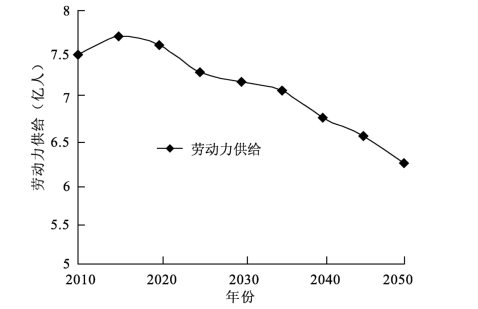
图11-1　劳动力供给下降趋势示意图

首都经贸大学的齐明珠博士运用要素预测法按照总和生育率TFL分别等于1.6和1.8两种情形对我国2010—2050年劳动力供给与需求进行了预测（见图11-2）。^[6]

图11-2　劳动力需求及TFL=1.6和1.8时劳动力供给趋势示意图

由图11-2可见，按TFL=1.8预测的数据与结论和^[7]基本一致，如果按TFL=1.6预测，未来劳动力供给下降的趋势更加严重。对照需求曲线，劳动力缺口将日趋明显，成为制约社会经济持续发展的瓶颈（见图11-3）。

图11-3　TFL=1.6和TFL1.8预测方案下劳动力供给缺口示意图

为了清晰地说明延迟退休方案既能够缓解未来劳动力供给不足，又不至于引起劳动力过剩，本文首先将按TFL=1.8和TFL=1.6的预测数据取平均值，得到若不实施延迟退休方案，未来各年份劳动力缺口的平均值。然后按照表11-2中各年份各类延退人群的增量倍率系数an，bn，cn，并且根据齐明珠对我国2010—2050年劳动力供给与需求预测中的数据，算得-y=26806.24万人，按照劳动力增量模型假设，α=1/3，β=1/6，γ=1/2，计算Sn，数据见表11-3。

表11-3　延退前劳动力缺口与延退后劳动力增量预测对照

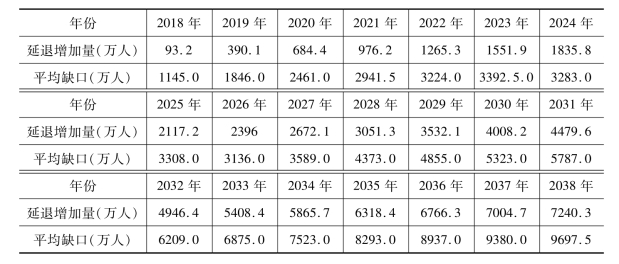
续表

图11-4直观地给出了延退方案带来的劳动力增量为补充未来劳动力缺口所做的贡献。

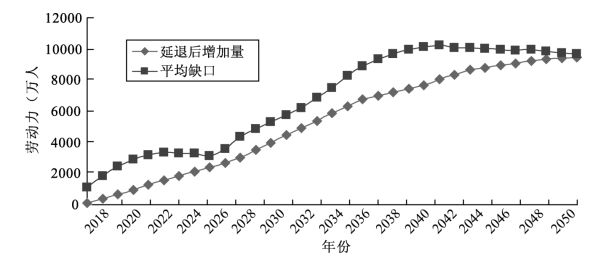
图11-4　劳动力缺口与延退后劳动力增量的预测示意图

从图11-4可以看出，实施延退方案后劳动力增加，大大缓解了由人口老龄化引发的劳动力不足，而且随着时间的推移，增量与缺口逐渐靠拢，达到劳动力供需平衡，这对社会经济持续稳步发展有着重要的意义。同时，我们可以看到，增加量曲线始终在平均缺口曲线下方，这就意味着在实施延退方案的未来30年进程中，劳动力不足现象将始终存在，一方面说明延迟退休不会引发劳动力过剩，造成大面积失业；另一方面，未来劳动力成本也将会持续攀高，这是人力资源管理中值得重视的一个现象，正因为如此，实施延迟退休，增加劳动供给，才能逐步消除劳动力不足，最终达到供需均衡。

（二）关于劳动人口占总人口的比重

劳动人口占总人口的比重并不是恒定的常数，每年不尽相同。设第n年该比重为ηn，则

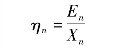
其中：En为执行原退休方案的劳动人口，Xn为总人口。

按上一节的计算，因实施延迟退休的新方案，劳动力增加了Sn，但总人口未变，所以劳动人口占总人口的新比重为

显然σn表示新增的比率。估算En需要相关的数据资料。

还是以我国2010—2050年劳动力供给与需求预测^[8]为例，取其中2018—2050年15—65岁的一段数据wn（n=1，2，L，33）。容易算出wn的平均值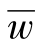，并且是44—65岁数据的平均值。运用回归分析，给出回归估计

其中的δ0为比例回归系数，计算值为δ0=-0.00675。

wn是劳动力的供给量，或称劳动年龄人口，并非实际的劳动人口。En是执行原退休方案的实际劳动人口，En当然要比wn少。可以做一个大致的折算：15—65岁含51个年龄，18—49岁含32个年龄，该年龄段的劳动力的供给量大致为（32/51）wn，其中女工人占比α，故女工人的实际劳动人口为（32/51）αwn。同理，女干部、男职工的实际劳动人口分别为（37/51）βwn和（42/51）γwn。所以

在前面已建立劳动力增量Sn与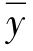的关系，得到

两者相除，可得

以回归估计代替其中的wn，归并系数，可得

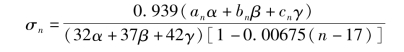
其中an，bn，cn为劳动力增量的倍率系数。

为了测算具体数据，估算三类人员所占的百分比α，β，γ。按男女比例1∶1、工人干部比例2∶1估计，可取α∶β∶γ=2∶1∶3，代入上式即得

运用这一公式和表11-2的数据，计算出每年的劳动人口占总人口比重的新增比率σn，如表11-4所示。

表11-4　劳动人口占总人口比重中的新增比率

（三）关于养老保险基金的收支变动及养老金替代率变化

关于养老保险基金的收支变动及养老金替代率变化的计算表明，延迟退休方案实施后，由于养老保险基金产生了收支顺差量，因此有效降低了其赤字风险。但是，基于我国国情和历史因素，养老金替代率必须控制在合理的区间内。替代率过低意味着退休职工的生活水平大幅度下降，与“收入倍增”的收入分配制度改革目标相悖；替代率过高，养老金赤字风险难以规避。本文的计算结果为55%～60%之间。如果国家经济发展状况良好，中央财政收入增加，增加对养老保险基金的扶持，养老金替代率高于60%也是完全可能的。

（四）延迟退休而不提高养老保险缴费年限的方案设计及其社会利益整合效应分析

1.方案

本方案（下称“第二方案”）有三个要件。第一要件是以本章第二节设计的渐进式延迟退休方案为基础，即：从2018年开始，用20年时间、分两阶段逐步实施，至2038年实现男女均65岁退休。实施步骤为：2018至2028年，女工人每年延迟一岁退休、女干部每1年延迟0.5岁。从2028年开始，男女均每1年延迟0.5岁退休，至2038年实现男女65岁同龄退休。

第二要件是职工达到现行国家规定的退休年龄后的延退期间，既不领取养老金，也不缴纳费养老保险费用。

第三是参照OECD国家退休与养老保险制度改革的主要做法在现行国家规定的退休年龄到65岁之间实行有条件弹性退休。比如：女职工达到60周岁；工作条件艰苦的劳动者（包括高纬度地区劳动者，矿山、井下危险工种劳动者，劳动条件恶劣易引发职业病的劳动者）；体弱多病者，可提前退休。实行弹性退休的不得再从事其他有收入劳动。

实行弹性退休不仅要有条件限制，且养老金的领取也应该参照OECD国家的做法实行区别对待，达60岁提前退休者才可领取一定比例养老金。比如美国最早62岁时退休可领取70%的法定养老金，此后每推迟一个月退休，养老金按比例上涨。西班牙的退休年龄制度规定：工人于60至65岁区间内退休，每早一年退休其养老金收入要降低8%。德国则规定提前退休领取了部分养老金并取得其他收入的仍需缴纳养老保险费。这些都可作为我国政府制定弹性退休有关实施细则的重要参考，使弹性退休制度符合我国的实际情况，既鼓励有条件的劳动者延迟退休，又有效抑制提前退休。

2.经济效应分析

关于延迟退休年龄而不提高养老保险缴费年限及有条件弹性退休方案的经济效应仍从个人视角、企业（雇主）视角和国家视角三个方面分析：

（1）从个人视角看。渐进式延迟退休年龄意味着职工少领取0.5～15年的养老金（开始实行时最少的只延迟了半年退休），多缴纳0.5～15年的养老保险。这一进一出对个人讲是不小的损失。虽然对高收入人群而言由于在职收入远大于养老金，足以弥补这笔损失，但对大多数中低收入者而言，这是一笔明显的亏空。笔者的民意调查中高达73.82%的被测试者不支持延迟退休，主要归因为个人眼前的利益受损。

本第二方案提出延迟退休年龄而不提高养老保险交费年限，单纯从经济角度看，对劳动者的眼前利益损失并没有减轻多少。研究表明，我国将退休年龄推迟到65岁，每年可以弥补养老统筹金缺口200亿元，其中增收的养老保险仅有40亿元。^[9]从整体看，目前我国的养老金替代率尚处较低水平（替代率是指全社会劳动者退休前后收入的比率，不代表某一行业，更不能体现某个个体退休前后收入的比率），全社会整体的养老金水平远远低于在职收入的一半，即替代率均低于50%。而养老保险个人缴费的部分只占在职工资收入的8%，即相当于养老金的1/6。因此延迟退休年龄而不提高养老保险交费年限对劳动者个人来说主要不是经济利益的变化，而是相对于第一方案既晚领取养老金，又多缴纳养老保险的一种心理补偿，能获得较多人群的认可。这从笔者的民意调查中可得到印证（见表11-5、表11-6）。

表11-5　各个职业人群对延迟退休接受态度分布（方案一）

表11-6　各个职业人群对弹性延迟年限且延迟年份不交保险接受态度分布（方案二）

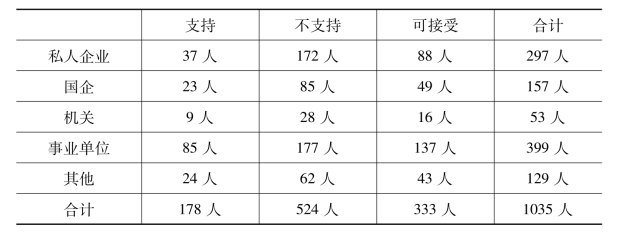
表11-7　第一方案与第二方案民意调查比较

转换成表11-7可看出，支持者从第一方案的7.63%上升为第二方案的17.20%，可接受者从25.51%上升为32.17%。第二方案中支持与可接受者合计达到49.37%，接近一半，这将大大减小推进延迟退休这一举措的阻力。

表11-8　不同职业群对第一方案与第二方案的态度对照

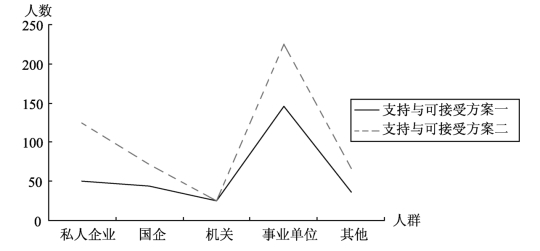
图11-5　不同职业群对第一方案与第二方案的态度对照

从职业分布来看，对第二方案的支持率和认可度除机关组（反对的样本数没有变化，支持的上升7.55%，故而可接受的下降了7.55%）都有明显上升，支持与可接受的合计上升20.20%。其中私企与其他劳动者支持与可接受的合计，分别上升了25.25%和23.25%。均高于平均上升度20.20%（见表11-8）。说明私企与其他劳动者对缴纳劳动保险费比机关、事业单位的职工有较高的关注度。这与目前机关、事业单位尚未普遍缴纳养老保险有关。随着机关、事业单位养老保险制度的改革从2014年10月1日开始实施，机关、事业单位对第二方案的支持与可接受度将会有一定程度的提高（见图11-5）。

从年龄分布来看，支持率上升较多的是46—51岁年龄层，可接受选项比例变化较大的是31—45岁年龄段。这与不支持延迟退休者年龄分布呈正相关特点。也就是说，反对程度较高的年龄段，对第二方案的支持与可接受度的正向变化也最大（见表11-9、表11-10、表11-11、图11-6）。

表11-9　各个年龄人群对延迟退休接受态度分布（方案一）

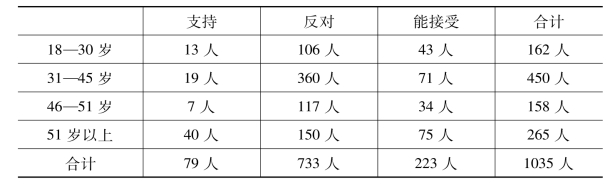
表11-10　各个年龄人群对弹性延迟年限且延迟年份不交保险接受态度分布（方案二）

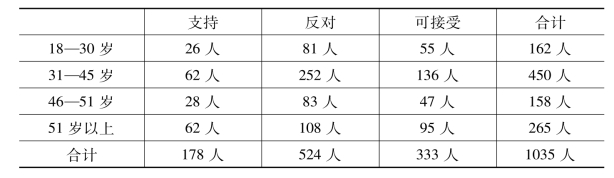
表11-11　不同年龄层对第一方案与第二方案的态度对照

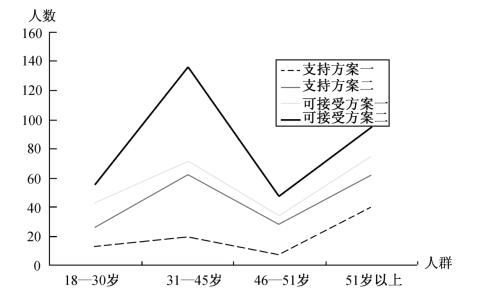
图11-6　不同年龄层对第一方案与第二方案的态度对照

表11-12　样本年龄分布

从学历层次来看，不同学历层对第二方案的支持与可接受度都高于第一方案，平均认可度上升20.19%。其中研究生及以上学历的人群，因原来对延迟退休的支持和可接受度本来就略高于其他学历层，因此其对第二方案的认可度只上升13.94%，但其绝对比例达到了63.63%，为各学历层的最高比例。不同学历层对第一方案与第二方案态度见表11-13、表11-14、表11-15、表11-16和图11-7（支持与可接受选项合并计算）。

表11-13　各个学历人群对延迟退休接受态度分布（方案一）

表11-14　各个学历人群对弹性延迟年限且延迟年份不交保险接受态度分布（方案二）

表11-15　不同学历层对第一方案与第二方案态度对照

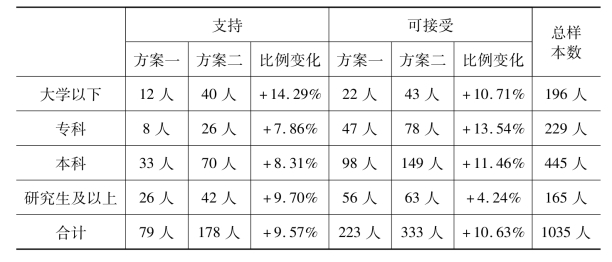
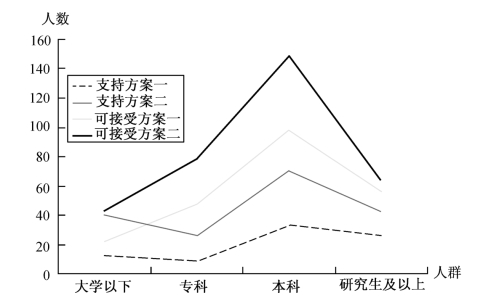
图11-7　不同学历层对第一方案与第二方案态度对照

表11-16　不同学历层对第一方案与第二方案态度对照（支持与可接受选项合并计算）

从收入分布来看，不同收入层对第二方案的支持与可接受度都高于第一方案，认可度提高的比例与收入分布成反比，收入低的对第二方案的支持与可接受度提高的比例，大于收入高的人群。但从绝对比例来看，年10万元以上的高收入人群对第二方案的认可度更高，支持与可接受度的达到了81.81%。不同收入层对第一方案与第二方案态度见表11-17、表11-18、表11-19、表11-20和图11-8（支持与可接受选项合并计算）。

表11-17　不同收入层对第一方案与第二方案态度对照

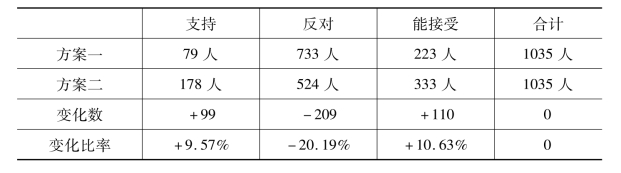
表11-18　各个收入人群对延迟退休接受态度分布（方案一）

表11-19　各个收入人群对弹性延迟年限且延迟年份不交保险接受态度分布（方案二）

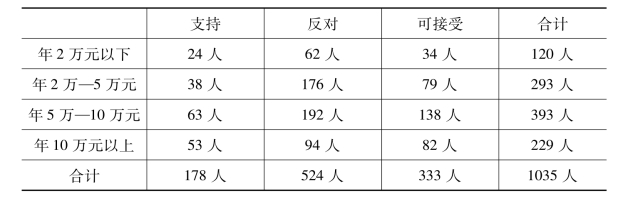
表11-20　不同收入层对第一方案与第二方案态度对照（支持与可接受选项合并计算）

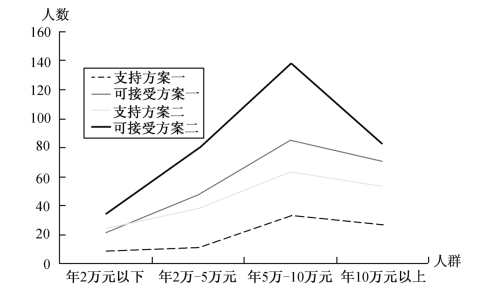
图11-8　不同收入层对第一方案与第二方案态度对照（支持与可接受选项合并计算）

从不同职业、不同年龄、不同学历和不同收入的人群对第二方案的支持与可接受度来看，不同的社会利益群体，都希望延迟退休年龄的改革举措应循序渐进，充分兼顾不同利益群体的切身利益，希望按第二方案实行渐进式延迟退休年龄与弹性退休。同时，从被测试者对第一方案与第二方案的态度变化比较来看，广大劳动者，只要政府在利益整合过程中充分考虑到不同群体的利益诉求，公平、公正地照顾到绝大多数人的利益，并做好各种方案的宣传、解释工作，延迟退休年龄这一举措也会得到大多数劳动者的支持与认可。

（2）从企业视角看。因为机关、事业单位养老保险制度的改革已经从2014年10月1日开始实施，因此本章讨论的企业，实际已包含改革后的机关、事业单位，故而用“雇主”较为贴切。

实行渐进式延迟退休年龄，而不提高养老保险交费年限及有条件弹性退休方案，最直接的受益者将是雇主。基本养老保险缴费标准中个人只缴纳在职工资的8%，而雇主需缴纳雇员在职工资的20%。因各地政府的劳动与社会保障部门会规定当年职工的最低缴费基数，因此，有的缴费基数会大于雇主实际支付给员工的工资。随着职业年金的陆续推行，雇主的负担无疑会更重。延迟退休期间不缴纳养老保险，不仅仅是政府少收入了养老保险金，雇主少支付了养老保险金这笔经济账。因为养老保险金总额只是雇员工资的28%，而晚领取的养老金大约是养老保险金的近2倍（目前替代率近50%）。政府推行延迟退休增加的收入约减少1/3，这里只就实行渐进式延迟退休年龄，而不提高养老保险交费年限，对雇主的经济效应进行分析。

在前面，我们分析了延迟退休年龄会不利于人力资源更新，不利于年轻人就业。民意调查显示：认为不利于年轻人就业的（选项4）占了最大比例63.19%，认为不利于人力资源更新的（选项3）占了第二位45.22%。数据分析发现，不同职业、不同年龄、不同收入、不同学历层次都集中反映了对这两个选项的较高关注度。由此推论这也是广大雇主关注点（见图11-9）。

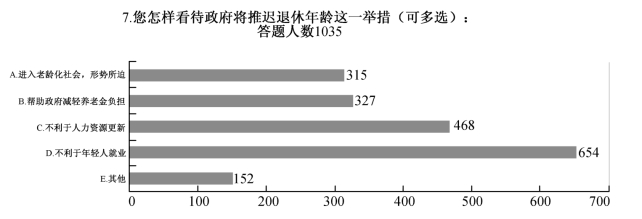
图11-9　您怎样看待政府将推迟退休年龄这一举措

目前，我国经济形势严峻。中国国际经济交流中心信息部部长徐洪才于2015年03月11日在《光明日报》上发表了《中国2015：经济形势分析、展望与建议》，分析了我国经济当前存在的主要问题，与本文相关的问题有：（1）经济增长面临下行压力，与2014年相比，增速同比回落1.9个百分点；（2）物价涨幅低位徘徊，出现轻微通货紧缩，消费增长小幅回落；（3）就业形势面临结构性问题，未来几年，中国劳动力适龄人口比例将下降，重点群体就业形势依然严峻；（4）国际收支趋向基本平衡，跨境资本流出快速增长，外汇储备增长显著放缓，跨境资本流动由流入转向了流出；（5）增长动力趋缓，固定资产投资下滑，增速同比较2014年回落4.2个百分点；（6）外贸形势疲弱；（7）房地产市场，2014年年底，增速同比下滑9.3个百分点，商品房销售面积增速同比下滑24.9个百分点，商品房销售金额增速同比下降32.6个百分点。

经济形势的严峻，人力成本的不断提高，使雇主不仅担忧多缴纳养老保险，还担心雇员的结构问题，工业4.0即将来袭的第四次工业革命也迫切需要补充掌握新技术、新工艺的新职工。

在2015年11月10日召开的中央财经领导小组第十一次会议上，习近平总书记提出了“供给侧结构性改革”概念：“在适度扩大总需求的同时，着力加强供给侧结构性改革，着力提高供给体系质量和效率，增强经济持续增长动力。”李克强总理17日在主持召开“十三五”《规划纲要》编制工作会议时再次强调，要在供给侧和需求侧两端发力促进产业迈向中高端。“供给侧结构性改革”必然为经济持续增长带来动力，然而技术的进步、行业结构的调整，也必然会带来“供给侧”劳动岗位供给量与结构的变化，对新人的需求加大，对老人的需求减小。这对延迟退休的负面影响也是不容忽视的。

如此种种，都影响着雇主对延迟退休的价值判断，增加着对推行延迟退休举措的舆论压力。因此采用渐进式延迟退休年龄而不提高养老保险交费年限的二方案将减轻雇主的经济压力，在利益整合的过程中兼顾包括雇主在内的各利益相关方，得到雇主的理解，减小来自雇主方的推行阻力。从而使渐进式延迟退休改革能得到大多数人的支持与认可。

（3）从国家视角看。其经济效应主要体现在延迟退休期间不缴纳养老保险对国家财政收入的影响及养老基金的收支平衡问题上。

按照第二方案进行测算，由于其中的第一和第三条件与第一方案中相同，变化的只是第二个条件，即设第n年达到现行规定退休而延迟退休的人员数Sn，实施第二方案后，人均缴纳养老保险基金为0，故养老保险基金增加收入Sn un=0元。但同时，他们的养老保险基金依然减少支出Sn vn元，即第n年的养老保险基金仅增加了Sn vn元。

方案实施后的养老保险基金的盈亏与养老金的替代率有关，按照第一方案，替代率的合理区间在55%到60%之间，而且替代率达到60%时，养老保险基金的亏损只是得到较大缓解，但并没有消除。实施第二方案后养老保险基金的增加减少了Sn un一块，因此，要减少基金亏损，只能降低替代率。这里我们按替代率合理区间的下限55%进行测算。

假设某职工在职总收入为I，那么在养老金替代率为55%的水平下，其养老金则为0.55I，即vn可视同作0.55I；在现行养老保险缴纳标准下，un=0.28I，因此，vn/（un＋vn）=0.66，将其中对应于替代率为55%的补充量均乘以0.66，即可得到方案二在55%替代率水平下，养老基金的补充量，将其加到表8-6的养老基金缺口预测情况表中的对应数值，即得方案二在55%替代率水平下养老基金盈亏的预测情况（见表11-21）。

表11-21　方案二在55%替代率水平下养老基金盈亏的预测（亿元）

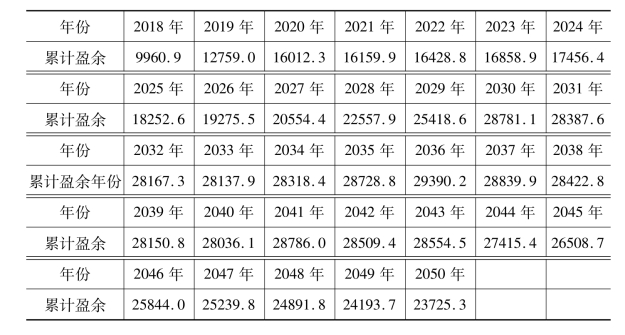
上述结果表明，在养老金替代率为55%的水平下，实施方案二，未来的养老基金将保持盈余，不会发生亏损。这一方面证明了在保证养老基金不产生缺口的前提下，方案二更能减轻企业和职工个人的负担，比方案一更优；另一方面说明了养老金替代率还有向上调整的空间。反过来说，方案一是取养老金替代率为55%—60%，方案二是说养老金替代率取下限55%时养老金收支仍能平衡。简言之，少收了5年养老保险，适当降低养老金替代率养老金收支仍能平衡（见图11-10）。

图11-10　方案一、方案二与未延迟退休累计盈余比较

3.社会效应

从上述问卷调查的统计结果看，实施延迟退休年龄而不提高养老保险缴费年限的方案其社会效应会优于第一方案。

“收入分配改革在整个改革中处于核心地位”，是“各项改革中最难啃的一块‘硬骨头’”。作为收入再分配内容之一的养老金缴费，直接影响公众对延迟退休的态度。上述调查显示，收入低的对第二方案的支持与可接受度提高的比例，大于收入高的人群。但从绝对比例来看，年收入10万元以上的高收入人群对第二方案的认可度更高，支持与可接受度的比例达到了81.81%。各类收入层对第一方案的支持和可接受度的比率与对第二方案的支持和可接受度的比率，合计由29.18%提高到49.37%，增加了20.19%，亦即接近一半的人群支持或可接受第二方案。因此，在退休年龄新老制度过渡期，实施延迟退休而不提高养老保险缴费年限的方案，有助于缓解社会矛盾，有利于延迟退休改革的顺利进行，有利于提升对社会主义核心价值体系的社会认同度。