碳排放的理论解释

　　目前,学术界关于碳排放影响因素的研究基本上是沿着两条主线进行的。

　　一条主线是围绕经济增长与碳排放之间的演变关系,不仅包括反映经济增长对碳排放的影响,而且也包括揭示经济增长与碳排放之间是否符合或存在碳排放环境库兹涅茨曲线(CKC)关系,即在经济发展的最初阶段,环境污染或退化随着人均收入的增加而加重,当达到一定的峰值后,则随着人均收入的增加而改善。但是关于经济增长与碳排放之间的EKC关系研究迄今为止尚未形成明确的定论。已有研究验证了二氧化碳和人均收入之间分别存在着线性、二次和三次递减形式关系,其中以支持倒U形CKC存在的有效证据居多,但是文献中CKC曲线峰值对应的人均收入差异很大。另一条主线是探讨碳排放与包括经济增长在内的多种影响因素或驱动力之间的关系,如人口、产业结构、能源结构、技术进步、城市化、政策制度等社会经济因素,这些研究更多地体现在实证层面。考虑到后一类研究所涉及的影响因素大多可以包含于广义的技术进步之中,因此本节主要利用IPAT方程来分析广义技术进步对碳排放的影响情况,同时也探讨了倒U形CKC形成的理论解释。

一、环境影响方程——IPAT

　　为了分析和表达人类活动对环境的影响,Ehrlich和Holdren(1971,1972) 在可持续发展的背景下,首次提出了环境影响方程即IPAT方程,将环境影响(I)归结为人口规模(P)、人均财富(A)以及技术水平(T)三个关键因素乘积的结果,建立起四者之间的关系式“I=P×A×T”。此后,虽然一些学者对其进行了改进,提出了不同形式的分析模型,如加入资源消费项(C)的ImPACT方程(Waggoner和Ausubel,2002),考虑人类行为(B)的IPBAT方程(Schulze,2002),引入社会发展状态项(S)的ImPACTS方程(徐中民等,2002),但是这类模型均存在着一些明显的局限性。首先,上述模型都属于评价框架,难以进行定量分析,如IPAT方程要求等式两边的单位严格统一,ImPACTS方程中的社会发展状态和管理的水平难以确定等。其次,这类模型均是通过改变某个因素,而保持其他因素固定不变的方式来分析问题,这就导致了各自变量对因变量的影响呈等比例变化,这显然与现实情况难以相符。最后,这类模型存在的最大缺陷是将人口、经济、科技水平、社会发展等因素对环境的弹性系数固定为1,因此其无法进行假设检验,也无法对是否存在EKC等二次或者更高次的相关性进行考察(刘宇等,2007)。为了克服上述不足,Dietz和Rosa(1994)将IPAT方程以随机的形式表示,建立了STIRPAT(stochastic impacts by regression on population,affluence and technology)模型,来弥补上述模型的缺陷。

　　尽管IPAT方程可能存在这样或那样的缺陷,但是由于其根植于生态原则中,可以比较清晰而简洁地说明或阐释环境影响如何随相关因素的变化而变化,因而本节主要从IPAT方程出发,来反映技术进步等因素驱动下碳排放的演变规律及其不同阶段的变化情况。而在后文的实证分析中则采用STIRPAT模型来进行研究。

　　作为人类活动对环境影响的基本分析工具,IPAT方程的具体的表达式为I=P×A×T。式中I代表环境影响,P代表人口规模,A代表人均财富,通常用人均GDP度量,T代表技术水平,通常用单位产出(GDP)产生的环境影响来表示。从物质流的角度,由于环境影响或污染物的产生从根本上与物质或能源的消费有机地联系在一起的,所以环境影响不仅可以用污染物排放来直接体现,也可以用产生污染物的能源或物质消费来间接表征。当环境影响用碳排放来表达时,则有:

　　CO₂=P×(GDP/P)×(CO₂/GDP)(4-1)

　　对上式两边同时取对数并对时间求导后可得:

　　=++(4-2)

　　由式(4-2)可知,碳排放的增长受到人口增长、经济增长和科技进步的综合作用,因此调控碳排放在理论上可以从上述三个因素的增长速度的控制入手。但是一般而言,人口的增长具有强大的惯性,虽然不少发达国家已实现了零增长或低速增长,但是对于发展中国家而言,人口仍处于快速发展阶段,即使采取严格措施控制人口增长,一般短时间内难以奏效,这就意味着人口的增长对碳排放的正向作用将持续相当长的时间。

　　经济增长通常是各个国家追求的目标,经济的增长必然导致能源消耗和碳排放的增加,试图通过降低经济增长率来实现碳排放增长速度的下降也是不现实的。因此降低碳排放的希望主要被寄托在技术进步这一活跃而又能动的因素上。考虑到碳排放强度同时受到结构调整、技术创新、政策调控和监督管理等多种因素的综合作用,所以其变化可以理解为包括这些因素在内的广义上的技术进步的结果。

二、倒U形CKC的形成

(一)碳排放强度的倒U形CKC

　　由式(4-1)和式(4-2)可知,要想降低碳排放的总量规模,首先需要通过技术进步降低单位产出的碳排放,即碳排放强度。而技术进步的大小和方向通常可以作为转变经济增长方式的先兆性判别指标,我们分三种情形对其进行讨论。

　　情形1:当>0时,技术进步以碳排放的增加为代价,必然会大大刺激二氧化碳排放的快速增长,同时也反映了经济增长方式极其粗放。

　　情形2:当=0时,技术进步对碳排放增加的正向作用达到临界点,此时碳排放的增加主要是人口规模增加和经济增长的结果。

　　情形3:当<0时,技术进步开始有利于减缓因人口和经济增长所导致的碳排放总量的增长速度,此时意味着经济增长方式也开始由粗放型向集约型转变。

　　因此实现碳排放强度从持续增加向稳定下降的方向转变,即从≥0向<0的转变,也就是跨越碳排放强度的倒U形曲线的拐点,促进碳排放强度的稳定下降,是实现碳排放规模缩减的前提条件。该过程使碳排放强度演变的倒U形曲线得以形成。

(二)人均碳排放的倒U形CKC

　　当技术水平不断提高或者碳排放强度持续降低时,人口增长和经济增长所导致的碳排放的增加就可以被逐步抵消。在正常的社会发展情形下,≪(非洲除外,因为许多非洲国家政局不稳,社会动荡,连年战乱,导致经济增长衰退,而人口又保持一定的增长速度),则保持在一定的区间内。根据发达国家的经验,当经济总量积累到一定程度后,经济规模一般保持较低的增长速度。在这种条件下,根据技术进步的大小可以再进一步讨论以下三种情形。

　　情形1:当0<≤≪<+时,由于相对较小,技术进步可以在短时间内抵消由人口增长所带来的碳排放的增加。

　　情形2:当<<<+时,技术进步不仅可以抵消人口增长所增加的碳排放,而且还可以额外抵消部分经济增长所增加的碳排放。在该阶段,经济增长对碳排放的增长速度发挥着主导作用,但碳排放的增长速度在逐渐下降。这一过程经历的时间要远远超过情形1所经历的时间。

　　情形3:当≤<+时,由CO₂/P=(GDP/P)×(CO₂/GDP)可推出=+,此时人均碳排放开始出现零增长,并且随着技术的不断进步而呈现出稳定下降的态势,从而形成了人均碳排放的倒U形曲线。这意味着技术进步导致的碳排放强度的下降速度能够平衡或抵消经济增长所导致的碳排放的增长速度。在该阶段,如果能够同时保持人口增长速度稳步下降或人口总量出现稳定乃至负增长,则可以加速人均碳排放下降趋势的提前到来。此种情形部分支持了 Stern(2004)的结论:在增长较慢的经济体中,减排技术进步能够战胜人均收入增长的污染排放规模效应。在相关实证研究中,已有不少学者采用人均碳排放证实了倒U形CKC的存在性。

(三)碳排放总量的倒U形CKC

　　当技术进步的作用足以抵消人口和经济增长所带来的碳排放总量的增长时,也就是节能或碳减排的技术进步具有主导作用时,即≥+时,≤0,碳排放总量实现了零增长,并进入到稳定下降阶段, 从而形成了碳排放总量的倒U形曲线。

　　由于≪,所以从<+向≥+过渡的时间一般较短,往往伴随着人均碳排放的稳定下降,所以碳排放总量稳定下降的阶段也将很快到来。此时,如果人口趋于稳定或=0,则人均碳排放与碳排放总量将同步下降。若<0,则会出现一种社会经济发展的极端情形,即碳排放总量的下降速度大于人均碳排放的下降速度,这在短期内或特殊情形下有可能出现,但从长期看,可能性不大,而且与实际情形和社会经济发展的一般规律不符。

　　由于技术进步总体上是一个随时间演变的渐进过程,这就决定了上述三个倒U形曲线依次出现的基本特征。当人口保持低速增长或零增长时,人均碳排放高峰和碳排放总量高峰将会接近或重合。尽管三个倒U形曲线规律是从时间尺度上获得的,但同样适用于经济尺度,因为经济增长也是时间的函数。

三、CKC的演化规律

　　综上所述,从长期来看,在技术进步的驱动下,一个国家或地区碳排放随着经济发展或时间的演变理论上依次遵循三个倒U形曲线的规律,即该演化过程需要先后经历碳排放强度的倒U形曲线、人均碳排放的倒U形曲线和碳排放总量的倒U形曲线(见图4-1)。或者说实现三大方向性的转变,即碳排放强度由增加向稳定下降方向转变、人均碳排放由增加向稳定下降方向转变、碳排放总量由增加向稳定下降方向转变。这与Renn等(1998)提出了质的增长(qualitative growth)所经历的三个阶段论,即单位国内产值资源消耗的连续下降阶段、人均资源消耗的连续下降阶段和整个国民经济资源消耗的连续下降阶段相类似,但更全面地反映了碳排放的阶段性演化轨迹。

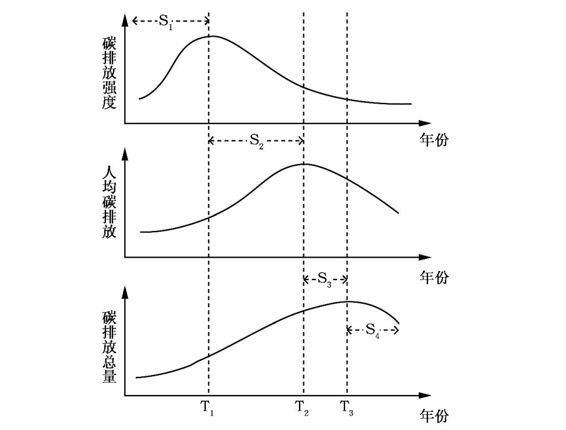
图4-1　三种倒U形CKC的演化趋势图

　　根据上述三个倒U形曲线规律,可以将该演化过程划分为四个阶段,即:碳排放强度高峰前阶段即碳排放强度上升阶段(图4-1中的S₁阶段)、碳排放强度高峰到人均碳排放高峰阶段(即图4-1中的S₂阶段)、人均碳排放高峰到碳排放总量高峰阶段(即图4-1中的S₃阶段),以及碳排放总量稳定下降阶段(即图4-1中的S₄阶段)。如果人均碳排放高峰和碳排放总量高峰在时间上重合,此时上述碳排放高峰的四个阶段就演变为三个阶段,这也可以看作是四个阶段的特殊情形。因此在现有的CKC实证研究中,选取不同的碳排放指标,如碳排放强度、人均碳排放和碳排放总量指标,实质上分别对应着不同的倒U形曲线。

　　在同一演变阶段,各指标的变化方向也不尽相同(如表4-1所示)。在S₁阶段,碳排放强度上升、人均碳排放上升、碳排放总量上升;在S₂阶段,碳排放强度下降、人均碳排放上升、碳排放总量上升;在S₃阶段,碳排放强度下降、人均碳排放下降、碳排放总量上升。在S₄阶段,碳排放强度下降、人均碳排放下降、碳排放总量下降。综上,要想实现碳排放总量的下降,实现环境与发展的协调,就要从根本上实现从碳排放强度、人均碳排放和碳排放总量同时上升,向碳排放强度、人均碳排放和碳排放总量同时稳定下降的转变。

表4-1不同碳排放演化阶段各碳排放指标的变化情况

S₁阶段

S₂阶段

S₃阶段

S₄阶段

碳排放强度

↑

↓

↓

↓

人均碳排放

↑

↑

↓

↓

碳排放总量

↑

↑

↑

↓

　　注:↑代表上升,↓代表下降。

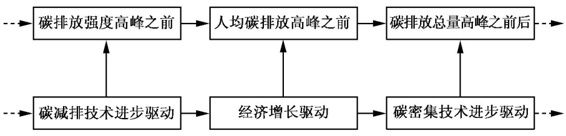
图4-2　碳排放不同演化阶段的主导驱动力

　　在不同阶段,碳排放的主导驱动力也明显不同(如图4-2所示)。在S₁阶段,虽然人口增长、经济增长和技术进步均对碳排放具有促进作用,但是碳排放增长更多地由碳密集技术进步驱动;在S₂阶段,虽然技术进步在一定程度上能够缓解碳排放增长速度,但是仍抵不上人口和经济增长所导致的碳排放增长速度,在该阶段经济增长对碳排放增长起着主导作用;在S₃和S₄阶段,碳排放主要由碳减排技术进步驱动(陈劭锋等,2009;陈劭锋,2010)。

　　需要说明的是,上述判断是基于碳排放强度持续降低或者技术不断进步的严格假定,即<0。在正常状况下,碳排放强度应该遵循这样的总体演变趋势。由于受到经济波动、结构调整、政策制度变动以及可能存在着技术或经济门槛(Neumayer,2002)等不确定因素的影响,碳排放强度可能会在个别年份或者短期内发生波动,并非一定保持持续下降态势。但只要在比较长的时期内,碳排放强度在总体趋势上呈现比较明显的下降趋势也是符合上述假定的。