我们将(4.3.3)式代入(4.3.2)式,可以得到πt新的表达式,如(4.3.4)式所示:

将(4.3.3)式和(4.3.4)式代入(4.3.1)式,并对it求一阶导数如(4.3.5a)式所示,经过推算即可以得到最优货币政策反应函数,以ipt描述,如(4.3.5b)式所示:

将 代入(4.3.4)式和(4.3.3)式即可以得到最优的货币政策操作在第t期将获得的通货膨胀率和产出缺口率,或者说最优状态下第t期实现的通货膨胀率和产出缺口率,分别以
代入(4.3.4)式和(4.3.3)式即可以得到最优的货币政策操作在第t期将获得的通货膨胀率和产出缺口率,或者说最优状态下第t期实现的通货膨胀率和产出缺口率,分别以 和
和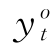 描述,如(4.3.6a)式和(4.3.6b)式所示:
描述,如(4.3.6a)式和(4.3.6b)式所示:

由(4.3.6a)式和(4.3.6b)式亦可以得知,合理、有效的货币政策操作可以完全抵消掉需求冲击对经济体的作用效果,最优货币政策操作下的通货膨胀率和产出缺口率都是通胀预期E tπt+1、实际有效汇率的对数、供给冲击 以及政策偏好λ的函数,而与需求冲击、需求函数中的其他信息以及其他宏观经济变量无关。
以及政策偏好λ的函数,而与需求冲击、需求函数中的其他信息以及其他宏观经济变量无关。
从另外一个角度来看,合理、有效的货币政策操作可以完全抵消掉经济体所承受的来自需求层面的冲击,并通过政策操作使得来自供给层面的冲击被产出缺口率和通货膨胀率合理消化,实现社会福利损失的最小化。这在本书第三章关于“泰勒曲线”的论述中已有阐述:正(负)的需求冲击将导致产出缺口与通货膨胀的同时恶化(改善),因此,可以通过合理、有效的货币政策操作将其对经济体的作用效果完全抵消掉;正的供给冲击将导致产出缺口与通货膨胀的反方向走势,可以通过合理、有效的货币政策操作获取产出缺口波动率与通货膨胀波动率的最佳组合,以实现社会福利损失的最小化。
同时,我们从(4.3.6a)式和(4.3.6b)式中亦可以看出通胀预期在货币政策操作中的重要性。相比“相机抉择”的货币政策操作风格,相对稳定的货币政策操作规则可以为公众提供相对稳定的通胀预期或通胀预期区间,而货币当局可以通过调节通胀预期达到调控经济的目的,以实现平抑通货膨胀压力并达到增进社会福利水平的目的。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















