计量经济模型分析什么比较简单

（一）S-VAR模型的构建

（5.3.2）～（5.3.4）式经修正后组成的宏观经济动态系统中含有变量之间的同期及滞后关系，我们考虑采用结构向量自回归（S-VAR）模型的估计方法进行参数估计。

首先，我们重审以下六个变量序列的平稳性检验结果。由于实际货币供给量的对数值lmt有明显的季节性，故采用Census X-12方法的加法模型^[4]分别对该序列进行季节调整^[5]。通过ADF检验（AIC与SC准则）与PP检验，我们发现，在10%的显著性水平下，我国通货膨胀率πt、产出缺口率yt、外国产出缺口率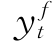以及利率水平it都是平稳序列，实际货币供给量的对数值lmt和实际有效汇率的对数值lqt经过一阶差分后平稳；鉴于此，我们将一阶平稳的外生变量lmt和lqt以其差分形式Δlmt和Δlqt写入实证模型。

本书动态系统中，将πt，yt和mt视为内生变量，将q1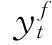，和it视为外生变量。其中，尽管mt是数量型货币政策工具的代理变量，由于现实中的实际货币供给量往往由货币当局相应操作与市场各种因素共同决定，故考虑将mt视为内生变量。

假定内生变量之间的相关性为：通货膨胀率受当期产出缺口率和前几期货币量影响、产出缺口率受滞后通货膨胀率影响、实际货币需求量受当期产出缺口和当期通货膨胀率及它们相应滞后期的影响。依照以上假设，将（5.3.2）～（5.3.4）式的基准模型调整为以下实证模型：

（6.2.2）～（6.2.4）式的系统可以矩阵形式表达如下：

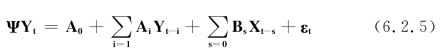
其中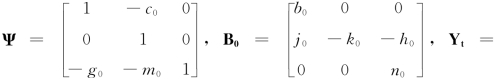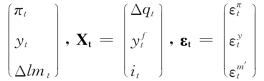：。在此假设，随机误差项εt中的三个序列皆为白噪声，且两两之间不相关。

（6.2.5）式即为本书实证研究的S-VAR模型形式，矩阵Ψ中恰好有三个为零的短期约束条件，且其对应的行列式无线性相关，故S-VAR模型可恰好识别，对其参数的估计往往通过相应的VAR简化式进行。由于矩阵Ψ可逆，（6.2.5）式可转化为VAR（p）模型：

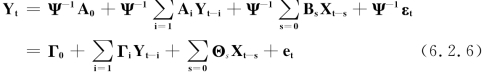
其中，Γ0＝Ψ-1A0，Γi＝Ψ-1Ai，Θs＝Ψ-1Bs，et＝Ψ-1εt＝，，）′。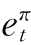

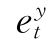因此，只要估计出简化式VAR模型中的Γ0，Γi，Θ和et，以及包含了S-VAR模型短期约束条件的矩阵Ψ，就能反向计算得到（6.2.5）式的参数估计结果。

在VAR模型估计中，无论变量是否同阶单整，只要满足所有根模的倒数在单位圆内，则模型稳定，其估计结果也有效。对（6.2.6）式的初步估计结果显示，当内生变量的最大滞后阶数为7时，能通过这一AR根检验。设定最大滞后长度为7阶即七个季度的滞后期。根据VAR（p）模型滞后长度的选择标准，AIC和HQ统计量结果选择6阶滞后，故对（6.2.6）式的VAR（6）模型进行参数估计。

标准VAR模型中将所有内生变量限定为相同的滞后阶数，然而现实应用中非对称滞后阶数的非标准VAR模型的拟合结果可能更优。非标准VAR模型的有效估计需采用SUR（相似无关回归）方法，我们可以多次调整各变量滞后期并对估计结果进行比较得到最优选择。将此估计结果进一步与标准VAR（6）模型的估计结果比较发现，最优选择的非标准VAR模型在方程拟合度、参数显著性及残差检验结果中的表现更优，如表6.2.1所示。相应的残差协方差矩阵如表6.2.2所示。

（二）实证的过程与结果

表6.2.1　（6.2.6）式非标准VAR模型的参数估计结果

续　表

注：***、**和*分别表示在1%、5%和10%水平下显著。

表6.2.2　（6.2.6）式非标准VAR模型的残差协方差矩阵

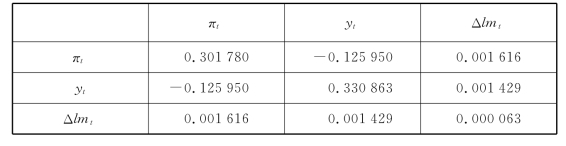
从表6.2.1我们可以看到，各方程的估计参数基本显著。本书重点关注的总需求方程与货币方程中利率it的参数估计值-0.562（即-h）和-0.008（即n）在5%的水平下显著。这表明在本书的宏观经济动态系统中，同业拆借利率水平的上升会抑制总需求，导致实际货币需求量减少。根据表6.2.1和表6.2.2的估计结果可分别写出（6.2.6）式的各参数矩阵et，Γ0，Γi和Θ。

可逆矩阵Ψ满足Ψ-1Ω（Ψ-1）′＝E（ete′t），其中Ω＝（）I，I为单位阵，且E（ete′t）即为表6.2.2所示的残差协方差矩阵，故可计算得到唯一解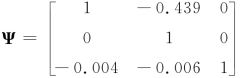。对照（6.2.5）式，可以得到m0＝-0.006，m2＝0.003，这表明在样本区间内，滞后两期产出缺口上升反映的市场总需求增加将带来当期实际货币量的增加，而当期产出缺口上升将带来当期货币量的紧缺。

根据εt＝Ψet，可计算出（6.2.5）式中样本区间内每个季度的残差可得到货币量的水平冲击以及相应的冲击波动率和。