实物期权理论的发展

1.研究领域不断拓展

（1）国际的研究领域

实物期权的应用研究从20世纪80年代中期开始兴盛。因为许多自然资源如铜矿等都有相应的期货交易市场，所以初期的实物期权主要集中于此。研究的便利也在于数据的可获得性。后来实物期权的思想逐步被社会所接受，其应用领域也逐渐拓展，涵盖各个不同经济领域。现在实物期权的研究可分为：房地产开发的实物期权、信息与生物技术的实物期权、竞争与战略的实物期权、制造与存货的实物期权、自然资源的实物期权、研究和开发的实物期权、股价评估的实物期权、技术创新的实物期权、风险投资的实物期权等。

将国际实物期权的各个研究领域及代表性文献归纳为表3-3，主要参考Trigeorgis（1993b）、Lander ＆Pinches（1998）、Miller ＆Park（2002）和冯邦彦（2003）的相关研究。

（2）国内的研究领域

实物期权的概念首先被国内学者陈小悦等（1998）在《实物期权的分析与估值》一文中引进，该论文属于综述性的文章，实物期权的基本分类、实物期权估值的离散方法和连续方法都得到了较详细的阐释；随后，探索性的研究，由黄凯（1998）在企业的战略投资决策领域予以尝试。伴随着中国经济改革开放的步伐，研究实物期权的热潮在国内金融、管理各领域开始了，出现了一系列研究成果，涵盖国外实物期权研究的几乎所有领域。表3-3归纳了主要研究领域和代表性研究文献。

综上所述，国内实物期权理论研究已涵盖中国经济生活的各个主要领域。不仅研究领域广，而且实物期权的模型也在不断丰富；研究方法已从简单的套用和修正经典模型向纵深发展，逐步把市场的不完全性、博弈因素纳入实物期权的分析框架。也许和中国的金融实践水平相关，实物期权理论研究切合实际应用的还不多，需要在工程层面、技术层面进一步深入探索研究。

表3-3　实物期权领域的经典文献

2.实物期权方法的发展

基于实物期权和金融期权的相似性，早期的实物期权方法研究主要把金融期权的定价模型，稍加改造后应用到实物期权领域中，对各种实物投资决策进行分析，发现一些新的有意义的结论；之后，实物期权的独特性、不可交易性、复合性、非独占性开始进入越来越多学者的研究视野，开始分析实物期权的建模基础、实物期权的复合博弈理论。同时，实物期权研究背景也放宽至不完全市场。

值得注意的是，由于大多数实物资产是不可交易的，如果简单套用作为金融期权定价理论的核心的无套利思想，不能形成无套利的有效复制策略。因为资产的可交易性是套利机会不存在的前提。因此，补救的办法是假定市场是完全的，且能够通过一个投资组合复制所有实物资产的收益，进而通过投资组合规避风险，Cox ＆Ross（1976）首先通过这一方法为不可交易的衍生证券进行定价。然而，实物资产的孪生证券却不容易找到，有时不可行。Trigeorgis（1996）提出了一个替代策略，寻找与实物资产高度相关的资产代替。还有一个原理很直观，但操作方法却很繁。分解法由我国学者扈文秀等（2005）提出，其基本思想是通过对决定实物资产价值的因素层层分解，来寻找服从已知分布的不可交易资产的实物期权定价。

（1）复合期权理论

复合期权是期权的期权，是一系列权利的嵌套，适合于刻画序列决策的问题。

如对R ＆D项目、高科技项目的风险投资、企业并购策略，若前期的预定目标没达到，投资者将选择放弃下一期投资。Geske（1977，1978）启动了复合期权的研究工作，导出了两期复合欧式期权的解析解。当前复合期权理论研究主要集中于如何对简单复合期权进行扩展。

如何从二期复合期权向多期复合期权推广，这在理论上没困难，难点在于计算的复杂性会随着复合期数的增加而迅速增加，导致求不出解析解。迪克西特等（2002）的分析方法是，用动态规划方法和或有权益分析求解复合期权的偏微分方程，在一定的边界条件下可求出复合期权价值函数和执行阈值的解析解，但边界条件很难满足。Alvarez ＆Stenbacka（2001）基于马尔可夫泛函的格林表示，得到了复合期权通用的计算方法，可求出复合期权价值函数和最优执行策略。Lin（2002）给出了欧式多期复合期权的一般形式解，且利用近似方法求解，由于解的形式中存在嵌套的高维正态积分，求数值解计算量很大。

改进复合期权的数学模型。在简单复合期权中，仅考虑单因素情况，且假设资产价过程为几何布朗运动。在多期时，参数的敏感性会被放大，因此几何布朗运动假设需要改进。Buraschi ＆Dumas（2001）将布朗运动推广到了一般的扩散过程，并得到了复合期权定价公式。Geman，EI Karoui ＆Rochet（1995）以及Elettra ＆Rossella（2003）不仅将布朗运动推广到了一般的扩散过程，而且引入时变的波动率和利率两个因素，将复合期权模型扩展到多因素情形。Herath ＆Park（2002）在此基础上，研究多资产、多期的复合期权模型，并采用二项式方法来定价和分析。Trigeorgis（1991）提出用所谓的“对数变形的二项式数值分析方法”来定价复合期权，在数值计算方面有很好的一致性、稳定性。

当然，期权的价格也可以是随机的，这与经典的期权定价公式有很大的不同。Fischer（1978）最早研究了不确定执行价格的期权定价；在随机执行价格下的复合期权定价公式由Geske（1979）得到。

（2）期权博弈理论

期权博弈理论起源于对权证或可转债的研究，因为权证期权的执行策略会明显影响权证或期权的定价；因为权证的执行会导致企业发行新股从而影响已发行股票的价值，进而影响剩下的权证价值。期权和博弈论的结合产生了期权博弈理论。早期的实物期权忽视竞争因素或假设竞争因素是外生的，这显然不合理。因为实物期权的非独占性的特点，一家企业的收益肯定会受到其他企业的影响，这种相互影响必然会使最优投资策略发生改变。一个简单的理解是，加入竞争因素后，投资收益将下降，即：投资项目价值＝传统净现值＋实物期权价值-竞争的影响。要更深入理解这一问题需要将博弈论和实物期权方法结合起来进行相关研究。

Cournot（1838）在经典著作《财富的数学原理研究》中提出了博弈的基本思想，开启了博弈理论的研究序幕，引入了古诺均衡（Cournot Equilibrium）的概念；在此基础上，一个双人价格竞争博弈模型由Bertrand（1883）建立；Edgeworth（1925）则进一步发展、建立了一个垄断企业定价和生产的博弈模型。这些充满原创思想的原始模型，引起主流经济学界的广泛重视。

巨大的转变开始于Von Neumann ＆Morgenstern（1944）的著作《博弈论和经济行为》。在该文中，通用博弈理论的思想被提出了，作者认为博弈应加入到大部分经济议题中，并推演了博弈的标准式和扩展式，最后提出了两人零和博弈模型与合作的多人博弈模型。由此博弈理论进入主流学者的视野。另一个重要的贡献是由Nash（1950）提出的概念——“纳什均衡（Nash Equilibrium）”。“纳什均衡”表达了这样一个理念，每个博弈参与方都是在考虑了其他参与方策略基础上的最大化反应，非零和博弈模型建立了。这个模型已成为大多数经济分析的重要理论前提之一。均衡和博弈模型的关系得到了进一步的研究。Selten（1965）提出并证明了并非所有的纳什均衡在扩展形式的博弈中都是均衡的，由此建立了“子博弈完美纳什均衡（Sub-game perfect Nash E-quilibrium）”的概念，来解释依赖于不可信威胁的均衡；随后，不完全信息被纳入了纳什均衡模型，Harsanyi（1967，1968）利用一种标准博弈论技术来分析不完全信息下的博弈模型。在这个模型中，博弈参与方并不确定知道参数值，但是知道参数的可能分布，由此产生了利用贝叶斯法则选择的均衡策略，即贝叶斯-纳什均衡（Bayesian-Nash Equilibrium）。如何解释博弈双方同时是不完全信息和动态时的博弈行为，引导Kreps ＆Wilson（1982）建立了序贯均衡概念，Selten（1975）则通过颤抖的手均衡概念，以子博弈完美均衡概念来解决不可信威胁问题。历经上百年的发展，现在博弈论已经进入了经济学的各个分支，成为现代经济学的主要基石之一。

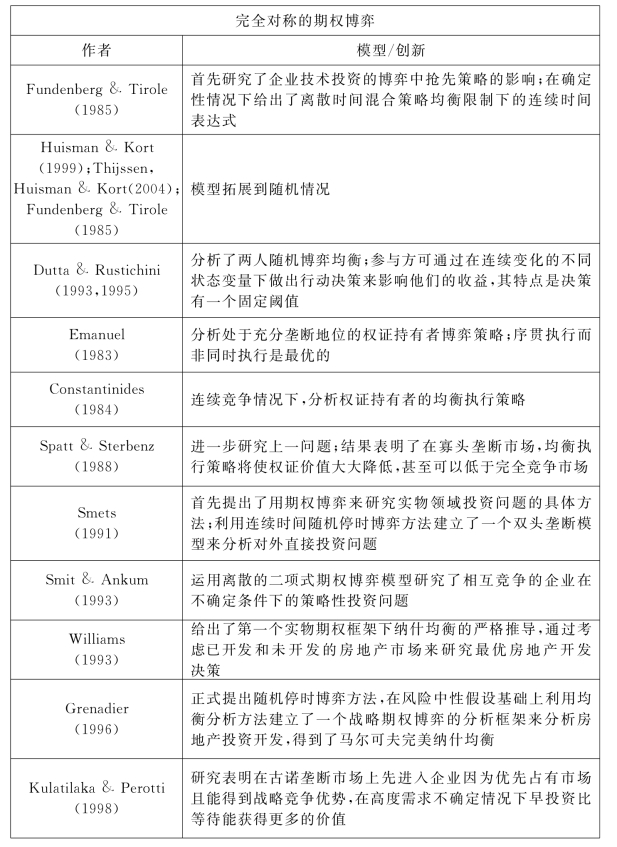
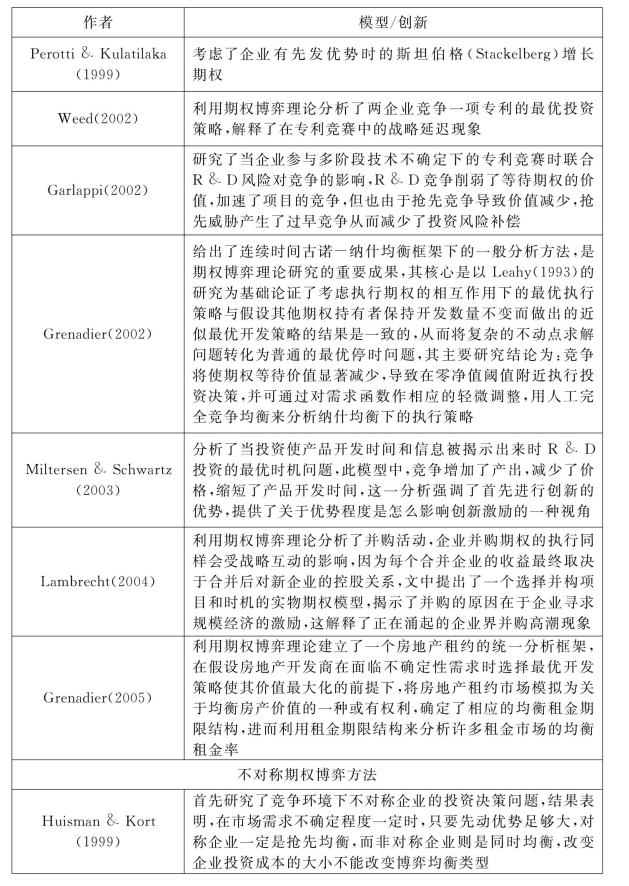
期权博弈理论的经典文献可分为：竞争各方是完全对称的和竞争各方是非完全对称的两类。期权博弈的代表性文献见表3-4。

表3-4　期权博弈的代表性文献

（续表）

（续表）

（3）模糊实物期权

不确定性或模糊性可以用随机过程来表示，那么很自然的模糊数学工具也可以用于不确定性的数学建模。首先用三角模糊数来描述资产价格的不确定性或模糊性，据此日本学者Yuji Yoshida（2003）开始进行最优投资策略的研究。模糊数观点下的期望和方差被Christer Carlsson和Robert Fuller（2003）引入传统的期权定价公式。同样的思想，二叉树模型中的上升概率和下降概率也可用三角模糊数来表示，由此Torricellli（2004）推导出了模糊二叉树期权定价模型。模糊期权定价的应用研究首先在R ＆D领域，由Juite Wang和WL Hwang（2005）开始，以处理在R ＆D项目缺乏可靠信息的情况下的最优决策问题。Hsien-Chung Wu（2007）用模糊数理论改造了经典的B-S公式，得到了模糊期权值。当然，在模糊数学的框架下，推导得到的实物期权值都是模糊数，即一个区间值。

国内的理论研究也另辟蹊径，安实等（2005）基于梯形模糊数假设，推导出了欧式实物期权B-S定价公式。应用研究有：陈晓红（2005）建立了模糊环境下高科技中小企业估值的期权模型。侯汉坡（2005）建立了一个模糊二项式期权定价模型，以解决企业并购过程中价值评估的难题。刘华明（2005）借用了模糊数的方法分析人力资源价值。赵振武（2006）基于现金流和投资成本是梯形模糊数的假设，建立了风险投资价值评估的期权定价模型。

（4）不完全信息下的实物期权方法

上面的研究，其基本假设都是市场是完全的，这一假设并不符合事实。实际上，真实市场中的投资决策大多是在不完全信息条件下做出的。关于不完全信息下的实物期权方法的研究才刚刚起步，有关文献相对较少。市场信息的不完全可分为两种：参与者之间的信息不完全和资产价格信息不完全。

不完全信息被纳入实物期权的分析框架的研究，最早由Grenadier（1999）开始。在文中，假定参与者可通过观察来推断其他人的私人信息从而选择行动策略，最终形成一个贝叶斯纳什均衡。研究结果表明，均衡结果是掌握信息最多的参与者首先做出行动，其他参与者依据先行者的信息依次做出决策，在绝大多数时候情况下会导致盲从行为，而这却是市场各方的理性选择结果。随后，Lambrecht ＆Perraudin（2003）将不完全信息和博弈两个因素同时引入实物期权的分析框架，建立了不完全信息条件下的抢先进入博弈模型，假设在专利体系下“赢者为王”，企业只知道成本，虽然不知道竞争对手成本，但知道对手成本的概率分布，随着时间的推移，如果竞争对手仍未投资，则可更新企业对其对手的信息，从而做出自己的投资决策。Williams（1995）的研究进一步加入了搜寻成本因素，建立了带搜寻成本的期权博弈模型。假设市场上买卖双方进行讨价还价，如果找不到这一最优价格，则在纳什均衡上达成一致，结果表明考虑搜寻成本参与人的决策会更迅速，从而未开发资产具有较低的市场价格。Grenadier ＆Wang（2005）则将委托代理理论引入不完全的期权博弈框架，假设实物期权分成管理者期权和所有者期权，研究结果表明投资决策有很大的惯性，且管理者的等待期权价值大于所有者等待期权的价值。模型的应用研究有，吴建祖等（2006）建立了市场不完全R ＆D投资的期权博弈模型，表明不完全信息延缓了企业的R ＆D投资。

市场信息不完全的另外一种表现是实物资产价格本身信息的不完全。如果资产价格信息不完全，那么价格过程可以被理解为带噪声的。Childs，Ott ＆Riddiough（2001）提出了这一思想，并用利用最优滤波理论来处理带噪声的价格过程，并分析了结果对投资决策的影响。结果表明，噪声会减慢信息到达速度，减少实物期权价值，由此激励会决策者搜寻额外信息。之后，作者分析了噪声价格过程的最优估计问题；在分别假设资产真实价格服从几何布朗运动、噪声服从和均值回复过程后，分析了远期期权的博弈策略，并运用于一个双头垄断的房产开发投资博弈模型的噪声影响分析；作者进一步拓展了模型，加入了风险贴息因素，分析有债务的资产评估和违约执行策略，结果表明，如果以最优价格为标准，有噪声干扰时更容易违约；在另外的标准下，则有噪声时不容易违约。

（5）人工智能实物期权

1943年，心理学家Mc Culloch W.和数理逻辑学家Pitts W.首次提出神经网络，至今其理论和实践已经获得了巨大进步。人工神经网络（ANN）是一种非线性非参数数学模型，是由神经元互相连接而成的网络，是对人脑进行抽象、简化和模拟的一种工程系统。这个模型具有学习的特性，优越性主要体现在复杂系统的建模上，广泛应用于在预测评价等方面。

神经网络的基本原理是模拟生物神经网络系统，其处理功能是由网路单元的输入输出特性、网络拓扑结构所决定的。与传统方法不同的是神经网络通过训练来解答问题。一个典型神经网络模型由输入层、隐含层和输出层三层神经元组成。相邻的两层之间的神经元通过一条带权值的弧线连接。通过神经网络求解问题，需要对其进行训练，这也称为网络学习。在训练过程中，通过每条连接权值的动态调节，使得实际输出和期望输出的误差不断减小。各变量之间的关系隐含于神经网络当中，形成一种非线性映射关系。神经网络的学习算法很多，比如反向传播算法、Hopfield算法等。在非线性预测中最常用的是B-P算法。

B-S-M模型及其衍生模型都属于参数化方法，参数化方法的不足是参数假设与真实存在差异，此差异会形成模型误差并削弱模型的适用性。例如资产价格过程服从布朗运动这一假设，已被大量研究证伪。为克服参数化方法的不足，应充分考虑金融市场的时变性、复杂性和非线性，从而更好地为期权定价。1994年Hutchinson J.，Lo A.和Poggio T.最早将神经网络模型引入到欧式期权的定价，这种定价方法的优势在于它是自适应的，适用于各种衍生工具。这种方法不仅适用于样本内数据，而且还适用于样本外数据，通过计算结果发现神经网络比线性模型表现更出色，神经网络可以记忆和学习之前的模拟或定价过程，提高效率，也可以结合遗传算法和小波分析等技术，以及人工智能、机器学习、并行计算等前沿领域的新型技术和研究成果。

人工神经网络期权定价方法通过建立一个市场数据驱动的非线性模型，使期权定价更客观、更准确，从而提供了更科学的定价依据。不足之处有：一是神经网络模型的结构设定难，即如何合理界定神经网络的层数，每层神经元的个数，还有之间的联系，不合理的神经网络结构会导致神经网络预测及自学习产生较大偏差；二是影响期权定价的因素，相关数据还应结合统计方法，找到所有重要的影响因素，以提高神经网络模型定价的精确度。总之应结合实际，开展组合神经网络期权定价方法的深入研究。