最优增长模型的经济增长要素

经济增长理论主要考察在完全竞争假设条件下一国经济随着时间稳定增长的行为。具体地说，考察一国长期经济增长与要素投入等有关经济变量的因果关系、经济增长进程是否具有内在减缓的趋势、不同国家之间随时间的推移而在增长率方面出现差异的原因。长期以来，经济学家们在经济增长的研究中，提出了诸多增长理论与模型。本章介绍具有代表性的哈罗德－多马经济增长模型、索罗经济增长模型和内生增长模型，它们对一国的长期经济增长及某福利后果都有各自的解释力。

一、哈罗德－多马经济增长模型

把经济增长作为一个独立的、专门的研究领域，是从英国经济学家罗伊·福布斯·哈罗德和美国的经济学家埃夫赛·多马开始的。哈罗德认为，凯恩斯的国民收入分析只是一种短期均衡分析，他只静态地考虑了投资变动引起的国民收入变动，没有动态地考虑国民收入变动对下一轮投资的影响，并且只以投资刺激需求增加从而实现总需求与总供给的本期均衡为目标，没有看到总供给的变化以及新的均衡，没有讨论经济体系的长期增长问题。在什么情况下一个经济体系可以实现长期稳定增长? 哈罗德认为，投资增加引起的国民收入成倍增加可以使本期实现就业均衡，但投资增加不仅刺激了总需求，引起国民收入的成倍增加(乘数原理)，而且刺激了总供给，引起了生产能力的增加，追加的生产能力带来了下一期国民收入的更快增长，更多的国民收入又会转化为更多的追加投资(加速原理)，如此累进不已。因而，本期的国民收入在下一期就不足以提供充分就业，从而总供求也不能保持均衡。所以，要实现充分就业，本期投资必须大于上期投资。

为了解决这一问题，哈罗德以凯恩斯的国民收入均衡理论为基础，提出了“资本－产出比”概念，利用它来推算第二期达到充分就业所需的追加投资，以使投资与国民收入的均衡增长相适应。这样，哈罗德在经济增长理论中引入了时间因素，并且用“比率分析法”(增长率、储蓄率)代替了凯恩斯的“水平分析法”(国民收入、储蓄与投资的水平)，从而将凯恩斯的理论长期化、动态化了。

20世纪40年代中期，美国经济学家多马以凯恩斯的有效需求原理为基础，独立地提出了与哈罗德经济增长模型相同的结论，因而一般把他们的增长模型通称为哈罗德－多马经济增长模型。

(一)哈罗德－多马经济增长模型的基本公式

哈罗德在建立其增长模型时做了如下假设: ①经济社会只生产一种产品，价格水平不变; ②只有劳动和资本两种生产要素，且两种要素不能相互替代，即企业的生产按照里昂惕夫生产函数进行; ③资本与产量的比率不变; ④不存在技术进步，也不存在折旧，且资本的增量等于投资; ⑤规模报酬不变，即: 生产任一单位产品所需要的资本和劳动的数量都是固定不变的; ⑥储蓄率不变，储蓄是收入的函数。

在这些假定基础上，用G表示经济增长率，Y表示国民收入，ΔY表示国民收入的增量，则有:

用v表示资本－产量比率，由假设③④有:

由此可得:

I=ΔY×v

用s表示储蓄－收入比率(储蓄率)，由假设⑥有:

由此可得:

S=s×Y

根据凯恩斯的国民收入均衡理论，在只包括居民户和厂商的两部门封闭经济中，经济活动达到均衡状态时，必有投资等于储蓄，即: I=S。所以有ΔY×v=s×Y，整理后可得:

式(9．9)就是哈罗德模型的基本公式，它说明: 在s和v固定不变的情况下，只要I=S条件成立，Y总能以一个稳定的速率(s/v)增长下去。更具体地说，在产品市场均衡条件下: 第一，经济增长率与储蓄率成正比，储蓄率越高，经济增长率也越高。第二，经济增长率与资本－产量比率成反比，即资本－产量比率越高，经济增长率越低。

(二)经济长期稳定增长的条件

问题是在现实经济活动中，s和v是否能固定不变? 或者说，经济能否自动地使每年储蓄保持一定数量，并使储蓄全部转化为投资，实现长期、稳定增长? 哈罗德认为还应该动态考虑相关条件。他用有保证的增长率、实际增长率和自然增长率来说明长期经济增长以及波动的原因。

1．实际增长率

实际增长率就是在事后统计中实际达到的增长率。G=s/v中的数字s、v如果是实际的统计数字，则G就是实际增长率。可以用公式表示为:

式中，GA是实际的增长率(即事后的增长率)，s A是实际的储蓄率(哈罗德假定它总是和预期的储蓄率一样)，v A是实际投资与实际收入增量之比。要注意的是，在一般情况下，实际增长率不能用哈罗德模型的基本公式来计算，这是因为实际经济状况并不满足哈罗德的前提假设。比如储蓄不等于投资或总需求与总供给不一定相等。

2．有保证的增长率

有保证的增长率是指投资者合意的经济增长率。用sw表示人们合意的储蓄率(称有保证的储蓄率)，用vw表示有保证的资本－产出比率(用投资－收入增量比率I/ΔY表示)，为了使投资者在保证实现最大利润条件下愿意按资本－产出比率增加投资，则有保证的经济增长率(Gw)应是:

哈罗德假定合意的储蓄率sw总是会实现的，即合意的储蓄率等于实际的储蓄率:s=sw，所以有:

根据公式Gw=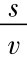，有:s=GA·v

根据公式Gw=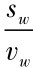，有:sw=Gw·vw

由于s=sw

所以有: GA·v=s=GW·vw

说明，如果实际经济增长率GA等于投资者感到满意的增长率，即有保证的增长率，则实际资本－产量比v，就一定等于资本家需要的资本－产量比vw。

3．自然增长率

自然增长率是指与人口增长率和技术进步所允许达到的最大经济增长率。从长期的经济发展来看，人口的增长和技术的进步对经济增长的影响是极其重要的。哈罗德－多马增长模型中引进了这两种因素，把人口增长归为劳动力增长、把技术进步归为劳动生产率增长。用n代表劳动力增长率，ε代表劳动生产率增长率，则经济的自然增长率(Gn)等于两者之和，即:

Gn=n+ε

4．实际增长率及其与有保证的增长率之间的关系

现在进一步考察一下GA·v=s=GW·vw，可见，只有当实际的资本－产量比v等于合意的资本－产量比vw时，实际增长率GA才会等于有保证的增长率GW。

如果GA＞GW，那么v就会小于vw。也就是说，一旦实际增长率大于有保证的增长率，企业的固定资产和存货就会少于企业家所需要的数量。这种情况促使企业家增加订货，增加投资，从而使实际产量水平进一步提高，使实际增长率GA与有保证的增长率GW之间出现更大的缺口。现有的实际经济增长就会在市场上的企业中产生相应的反应，使得GA进一步大于GW。

如果GA＜GW，那么v就会大于vw。也就是说，一旦实际增长率小于有保证的增长率，企业的固定资产和存货就会多于企业家所需要的数量。这种情况促使企业家减少订货，减少投资，从而使实际产量水平进一步降低，使实际增长率GA与有保证的增长率GW之间出现更大的缺口。现有的实际经济增长就会在市场上的企业中产生相应的反应，使得GA进一步小于GW。

由于实际经济中储蓄不一定全部转化为投资，或者说总产出与意愿的总支出不一定相等，所以GA和GW的完全一致仅是偶然的巧合，在继后的时期里，将出现累积性的经济扩张(GA＞GW)或经济收缩(GA＜GW)。因此，哈罗德得出结论，实际增长率与有保证的增长率之间一旦发生了偏差，经济活动不仅不能自我纠正，而且还会产生更大的偏离。这意味着，资本主义经济发展很难稳定在一个不变的发展速度上，不是连续上升，便是连续下降，呈现出短期经济波动的状态。只有当实际增长率等于合意的增长率时，经济才能保持在充分就业条件下的短期、稳定的增长。

5．自然增长率与有保证的增长率的关系

如果劳动力增长率n=1%，劳动生产率增长率ε=5%，则自然增长率为6%。这样，保证实现长期充分就业的均衡增长率就是6%。如果均衡增长率偏离自然增长率，就会使经济过程出现波动。

当有保证的增长率大于自然增长率，说明储蓄和投资的增长率超过了人口增长与技术进步所能允许的程度，这时的生产增长受到劳动力的不足与技术水平的限制，将会出现储蓄与投资过度现象，也就是社会总供给大于社会总需求，从而使经济呈现长期停滞的趋势。反之，当有保证的增长率小于自然增长率，说明储蓄和投资的增长率还没有达到与人口增长同步所允许的程度。这时，生产的增加不会受劳动力不足与技术水平的限制，生产者将增加雇用工人以扩大再生产，从而使经济出现长期繁荣的趋势。

由于哈罗德－多马模型是以里昂惕夫生产函数为基础进行讨论的，其函数的基本形式为: Y=F(K，L) =min(a K，b L)，a＞0且b＞0。由于固定比例，如果a K=b L，即可以利用的资本存量和劳动力恰好都被利用了。如果a K＞b L，那么只有(b/a)·L数量的资本被利用，剩余的资本被闲置。如果a K＜b L，那么只有(a/b)·K数量的劳动被使用，剩余的劳动力被闲置，即造成失业。由于里昂惕夫生产函数假设资本和劳动力之间无替代性，从而只要有保证的增长率和实际的增长率不等于自然增长率，就会使得经济增长不是连续上升，便是连续下降，呈现出剧烈波动的状态。

6．实际增长率、有保证的增长率与自然增长率的关系

当GA=Gw=Gn时，经济可实现连续的充分就业，可以实现长期均衡的增长，这是一种最理想的经济增长状态; 当三者不一致时，长期均衡增长几乎是不可能的。因此，常被称为“刃锋式”的经济增长，模型的理论意义大于实际意义。

哈罗德－多马模型是现代主流经济学意义下的第一个经济增长理论模型，哈罗德本人就是“凯恩斯革命”的参与者，参加过为凯恩斯写作《通论》做理论准备的学术讨论。这一模型开启了应用数理模型研究经济增长的先河，并把凯恩斯采用的短期静态均衡分析所提出的国民收入决定理论长期化和动态化，使经济增长理论的研究走上了一条正确的道路，是经济增长理论的第一次革命，同时它也是新古典经济增长模型的基础，对于经济增长理论的发展产生了巨大的影响。模型的政策启示是: ①前期储蓄必须全部转化为投资，才能使前期增加的收入得到全部实现。因此，经济是在长期、动态的过程中增长的。②完全竞争的市场经济中，由于GA=Gw=Gn三者达到一致的长期均衡增长可能性很小，只有通过政府的积极干预，才能避免经济增长过程中过于动荡。③在假定条件下，储蓄率成为经济增长的决定性变量。政府可以通过调节储蓄水平实现经济均衡增长。但模型过分强调经济增长的根本动力来自于资本积累、关于储蓄等于投资、劳动和资本不可相互替代、不存在技术进步等的假定不适用于发展中国家，在一定程度上限制了其对现实的解释力。

二、新古典经济增长模型[1]

以索罗为代表的新古典经济增长模型对哈罗德－多马模型进行了修正，放弃了该模型关于劳动和资本不可相互替代以及不存在技术进步的假定，将注意力集中在经济增长与资本积累、技术变革的联系，重新提出了自己的假设条件: (1)假定为两部门封闭经济，政府部门也被忽略，且社会只使用两类投入(资本与劳动)生产一种均质产品，可以是消费品，也可以是投资品; (2)劳动力按照一个不变的比率n增长; (3)储蓄总能转化为投资，即I=S; (4)生产的规模报酬不变。即专业化收益已经被全部利用，劳动、资本与技术以外的其他投入相对不重要; ⑤市场是完全竞争的，并且总是在充分就业的水平上运行，劳动和资本可以通过市场调节而充分地相互替代。根据以上修订与假设，模型从柯布－道格拉斯生产函数出发，分技术进步变与不变两部分进行递进讨论。

(一)不考虑技术进步时新古典经济增长模型的增长模型

1．增长模型推导

设有生产函数形式: Y=AF(K，N)

因不考虑技术进步，设A为1，有Y=F(K，N)

总产出增长的讨论在第一节有述。其中的索罗余值是该模型与哈罗德－多马模型的重要区别之一。由于人均产出增长更具讨论意义，假定一国全部劳动力都参加生产，由于规模报酬不变，将方程两边同除以N，有

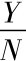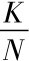令=y，=k

生产函数可以改写为:

y=f(k)

式中: y为人均产出; k为人均资本量; y=f(k)为一般形式，表示人均产出取决于人均资本量，人均资本量的增加会使人均产出量增加。但是，由于假设条件(2)，假定储蓄是收入的一个固定有分数s，人均储蓄为sy; 由于假定条件(4)，有要素的边际报酬递减规律存在，人均产出会以递减的速度增长。图9－1是生产函数y=f(k)的图示。现在要讨论的是人均资本量增长的决定因素。

图9－1 人均生产函数曲线

在一个只包括家庭部门和企业部门的两部门简单经济中，由于没有政府部门、没有对外贸易和资本流动，由假设条件(3)，经济的均衡为:

I=S

即投资或资本存量的增加等于储蓄。[2]一般地说，资本存量的变化等于投资减去折旧。当资本存量为K时，假定折旧是资本存量K的一个固定比率δK(0＜δ＜1)，则资本存量的变化ΔK为

ΔK=I－δK

根据I=S=s Y，上式可以写为:

ΔK=s Y－δK

上式两边同除以N，有

ΔK/N=sy－δk　(9．12)

另一方面，注意到式(9．12)有k=K/N存在，对上式两边取对数，则有lnk=ln K－ln N，又因为这些变量都是时间的变量，即lnk(t) =ln K(t) －ln N(t)，对上式两边对时间t求导，得[3]

式中的ΔN/N=n，为劳动增长率。于是上式用文字来解释就是: 人均资本增长率等于资本增长率减去劳动增长率。

等式两边同乘以K，有: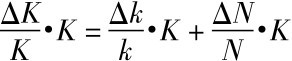，推出ΔK=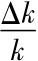·K+n K

上式两端同除以N，则有:

将式(9．12)、(9．13)合并，消去ΔK/N，于是

式(9．14)即为新古典增长模型的基本方程。它说明了资本随着时间的推移而变化的情况。公式表明，人均资本增加Δk等于人均储蓄sy减去(n+δ)k项。(n+δ)k项可以这样理解: 劳动力的增长率为n，一方面，一定量的人均储蓄必须用于装备新工人，每个工人占有的平均资本为k，这一用途使用的储蓄便为nk; 另一方面，一定量的储蓄必须用于替换折旧资本，这一用途使用的储蓄为δk。也就是说，人均储蓄sy扣除用于为每一新增人口提供平均的资本装备nk和替换折旧资本用去的部分δk后即为人均资本增加量Δk。总量为(n+δ)k的人均储蓄是资本积累的增加，被称为资本的广化，人均储蓄超过了(n+δ)k的部分导致了人均资本k的上升，即Δk＞0。根据假设条件，增加的人均储蓄总能转化为人均资本，这一人均资本量随着时间推移而增长的过程被称为资本的深化。因此，新古典经济增长模型的基本方程可以用语言表述为: 资本深化=人均储蓄－资本广化。结果，在技术进步等其他因素不变时，资本深化会带来人均产出的增长。

2．稳态分析

均衡经济的增长有两种情况: 第一种情况是人均产出的持续增加而带来的经济总量增长; 第二种情况是人均资本不变，人均产出并不增加，经济总量的增长只是因为人口的自然增长而增长。第一种情况称为经济的加速增长，第二种情况称为经济的稳态增长。

稳态是指人均资本k达到均衡数值并维持在均衡水平不变，在忽略了技术变化的条件下，人均产出y也达到了稳定状态的情形，如图9－2所示。

在图9－2中，y=f(k)代表人均产出随人均资本变化而变化的曲线，随着人均资本的增加，资本边际收益递减规律开始起作用，资本边际生产力递减，故f(k)呈图中向右上方倾斜且逐渐平缓的曲线形状; sf(k)是人均储蓄曲线，由于f(k)的性质决定了其图形也向右上方倾斜且逐渐平缓; 反过来，如果人均资本下降，则相反的情况就会出现。(n+δ)k表示资本广化，由于假定 n和 δ都是不变的常数，故(n+δ)k是条直线，它和sf(k)线相交于E点，表示经济在E点处于均衡状态，这时人均资本为k E，人均产出为y E。E点同时将人均产出y E分成两个部分: BE为人均消费部分，Ek E为人均投资部分。若经济运行在E点左边，sf(k) ＞(n+δ)k，即Δk＞0，表示随着时间的推移，人均资本k会持续上升，必有Δy＞0，一直到稳定状态k E为止。若经济运行在E点右边，则sf(k) ＜(n+δ)k，即Δk＜0，表示随着时间的推移，人均资本k会持续下降，必有Δy＜0，一直到稳定状态k E点为止。若经济运行在E点上，有sy=(n+δ)k，Δk=0，此时人均资本k就不再随着时间的推移而变化，如果没有技术进步，人均产出y也不再随着时间的推移而变化，有Δy=0，k=k E。这一状态代表了经济的长期均衡，E点被称为长期均衡稳态点。因此，离散形式的新古典增长理论模型中稳态的条件是:

图9－2 经济增长的稳态

sy=(n+δ)k　(9．15)

此时经济增长处于相对稳定状态，人均资本k和人均产出y是相对固定的，其增长率为零。但总产出量Y和总资本量K都在增长。因为劳动人口量N以n速度增长，因此，总产出Y与总资本存量K的长期增长率必须与劳动力数量N的增长率n相等[4]，即

ΔYY=ΔNN=ΔKK=n (9．16)

从上述分析我们可以看到，新古典增长模型的一个重要意义在于，不考虑技术进步时，有着相同的储蓄率、人口增长率和技术条件，也就是说有着同样生产函数的各国，最终将在同样的收入水平上趋于一致，尽管这一趋同过程可能十分缓慢。同理，从式(9．15)、(9．16)及其图9－2中还可以看到:

(1)k值越小(意味着资本越贫乏)，越有可能资本深化，故经济增长中穷国会快于富国; (2)s越高，sf(k)曲线越向上移动，从而使稳态下的人均资本和人均产出提得越高;(3)n越低，可使(n+δ)k曲线向右下方转动，从而使稳态下的人均资本和人均产出提高。(4)稳态中的总产出增长率等于外生的人口增长率n，独立于储蓄率s，不受储蓄率的影响。关于这一点，通过图9－3、图9－4还将看得更为清楚一些。

为简便起见，假定人均生产函数为y=f(k) =kα，其中α为介于0和1之间的参数，则由式(9．15)可知: skα=(n+δ)k，由此求得:

式(9．18)表明，若其他条件相同，储蓄率或投资率较高的国家由于人均资本量较高，因而人均产量较高，国民就比较富裕; 相反，人口增长率较高的国家通常比较穷。在这些国家，面对人口增长，为保持资本－劳动比率不变，需要把更大比例的收入用于储蓄和投资。这种资本广化的要求使得资本深化变得更加困难，从而使得人均资本量减少。

3．稳态的变化

稳态的变化是指外生变量s、n、δ等变化对稳态点的影响。主要表现在如下几个方面。

首先，储蓄率的变化会对稳态产生影响。这里考察储蓄率提高的情形，储蓄率下降的情形可以依此类推。图9－3中，最初人均储蓄曲线s0y与(n+δ)k曲线在E0点相交，E0点表示最初的经济稳态均衡，此时的人均储蓄为E0k0，人均资本量k0。当储蓄率由s0提高到s'以后，人均储蓄曲线s0y上升到s'y的位置。但人均折旧和人均资本装备之和(n+δ)k并未改变，因此有Δk＞0。随着时间的推移，有人均资本k会持续上升，一直到稳定状态k'为止。此时，人均储蓄曲线s'y与(n+δ)k曲线在E'点相交，E'点表示新的经济稳态均衡。新的稳态下，人均储蓄为E'k'，多于旧均衡的E0k0; 人均资本量为k'，也多于原先均衡时的人均资本量k0。显然，储蓄率的提高增加了稳态的人均资本量，新的稳态均衡时的人均收入大于旧稳态均衡时的人均收入。因此，储蓄率的提高还增加了人均收入。

由于E0点与E'点都表示稳态，所以，这里所提到的稳态变化不是指由稳态到非稳态，而是指旧的稳态点变化到新的稳态点，经济变化前后都是稳态。这就是说，储蓄率s的提高会使人均产出y的增长出现一个过渡期。如图9－3所示，储蓄率从s0增加到s'，人均产出y便会有从y0增长到y'的稳态水平的过渡，总产出的增长率也会有一个过渡期的变化。但过渡期结束以后，人均产出的增长率又会回到均衡的增长率，此时不能影响稳态下总产出的增长率n。

因此，对于E0到E'点的变化，还应必须从长期和短期两个视角对人均产出和总产出增长率两个问题进行考察。从短期来看，更高的储蓄率s会导致更多人均资本k的增加，从而导致人均产出y和总产出增长率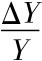的增加。图9－3中，当Δk＞0时，随着时间的推移， k0右移到k'时，必有y0上移到y'，同时引发ΔYY的增加。图9－4中(a)显示了人均产出y变化的时间路径; 同样随着时间的推移储蓄率s的上升导致了人均资本k上升，并使人均产出y以递减的速率增加，直到达到新的稳态为止。但是，从长期来看，由于k0对应的E0点和k'对应的E'点都是稳态点，按照前面关于稳态的分析，稳态中的总产出增长率是独立于储蓄率的，因此，尽管短期中总产出的增长率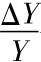会随着储蓄率s的增加引发的人均资本k增加、人均产出y增加而有提高，但长期中，随着(n+δ)k表示的资本积累的增加，总产出增长率逐渐降低，最终又回到稳态的人口增长水平n; 同时也提高了人均资本k和人均产出y的长期水平。图9－3中，k0右移到k'后不可能再增加，因而y0上移到y'后不可能再变化，此时引发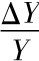增加的就只是式(9．15)描述的n。图9－4中(b)显示了总产出增长变化的时间路径: 储蓄率s的增加导致资本积累相应增加，从而带动了总产出的一个暂时性的较高增长率。但随着(n+δ)k表示的资本积累相应增加，长期中总产出的长期增长率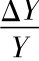最终会回落到人口增长率n的水平上。

图9－3 储蓄率提高对稳态的影响

图9－4 人均产出和总产出增长率随时间变化的轨迹

总之，新古典增长理论在这里得到的结论是，储蓄率增加不能影响稳态增长率，但确实能提高收入的稳态水平。也就是说，储蓄率的增加只有水平效应，没有长期增长效应。

其次，人口增长率的变化会对稳态产生影响。这里考察人口增长率提高的情形，人口增长率下降的情形可以依此类推。

新古典增长理论虽然假定劳动按一个不变的比例n增长，但当把n作为参数时，就可以说明人口增长对产量增长的影响。图9－5中，最初的经济位于N1点所表示的稳态均衡，此时的人口增长率为n1、人均资本量为k1。当人口增长率由n1提高到n2以后，(n1+δ)k曲线向左上方转动到(n2+δ)k的位置，(n2+δ)k曲线与sy曲线相交于N2点，N2点实现了新的稳态。由于sy曲线向右上方倾斜，(n1+δ)k曲线上升后的新的均衡点N2点一定低于N1点。比较N1、N2两点可知人口增长率由n1提高到n2后人均资本由k1降低到k2，人均产出由y1降低到y2，出现一个k与y同时下降的过渡期(短期)。因此，人口增长率n的提高降低了人均资本k与人均产出y的长期稳态水平。长期则如式(9．15)的描述: 总产出Y的增长率会收敛于n，并随n的变化而变化; n的上升对人均资本和人均产出的长期增长率都不产生影响。这一结论解释了发展中国家人均产量下降由人口增长率上升引起的现象和总产出水平由于人口增长率的上升而增加的现象，并且解释了两个储蓄率相同的国家，人均收入会由于人口增长率不同而不同的原因。

图9－5 人口增长率的提高对稳态的影响

上述分析表明，在没有技术进步的条件下，如果经济增长仅仅是靠资本积累，由于资本的边际收益递减，人均资本的增长将不同步于人均产出的增长，人均产出的增长、生活水平的提高最终还是会停滞。

(二)考虑技术进步时的新古典经济增长模型

上述分析未考虑技术进步，而是出于简化，令ΔA/A=0。而考虑技术进步正是新古典增长理论不同于哈罗德－多马模型的重要之处。现在考虑技术进步，即允许ΔA/A＞0来对人均经济增长进行讨论。

1．经济增长模型推导

考虑技术进步时，总产出的生产函数可以写成

Y=AF(N，k)

式中，A为技术，A可以在若干位置中以任意一种进入生产函数。一般地，给定资本与劳动，Y与A有正向关系。

A可以在若干位置中以任意一种进入生产函数。为了便于分析，常将生产函数写成如下形式[5]，并略去对柯布－道格拉斯生产函数的具体推导:

Y=F(AN，K)　(9．19)

上式中AN被称为有效劳动，此时，新古典经济增长理论对生产函数的假定就变为产出Y是资本K和有效劳动AN的一次齐次函数，则根据齐次函数的性质可以证明:

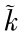对式(9．19)两边同乘以λ，有λY=F(λAN，λK)。又设λ=1/AN，则有Y/AN=F(1， K/AN)。记=Y/AN，表示有效劳动下的人均产出，=K/AN，表示有效劳动下的人均资本。于是，Y=F(AN，K)，可以改写为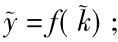有

假设技术进步率为g=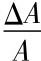，人口增长率为n=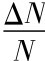，折旧率为δ。

ΔK=I－δK=s Y－δK，等式两边同除以AN，考虑上述假设条件，有

因为，对其两边取对数;有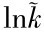=ln K－(ln A+ln N);又因为这些变量都是时间t的变量，即

ln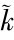(t)=ln K(t)－［ln A(t)+ln N(t)］，等式两边再对时间t求导，得

联立式(9．21)和(9．22)，有

推出

经济稳态的条件是: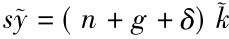。可见图9－6。

图9－6 引入技术进步的新古典增长模型

式(9．23)表明，考虑技术进步时，有效劳动下的人均资本增加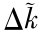等于有效劳动下的人均储蓄s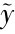减去(n+g+δ)项。(n+g+δ)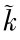项分为三个部分: n~k是为每一新增有效劳动人口需要新增人均资本的部分;是每一有效劳动人口的人均资本中需要折旧的部分;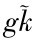是因为技术进步需要有效劳动人口新增人均资本的部分。

2．从图形及其文字分析中还可以得出的几点认识

(1)引入技术进步因素并没有使前述稳态分析的结论产生大的波动。

(2)由前述假定条件就可知，n、δ为常量。

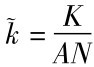(3)处于稳定状态时，由于，推出按有效劳动平均的资本的增长率为零，进而按有效劳动平均的产量~y=Y/AN的增长率也为零。

(4)引入技术进步因素后，人均产出增长率只取决于技术进步速度。由于Y=F(AN，K)，并以柯布－道格拉斯生产函数为背景[6]，整理后有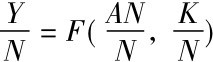;推出y=F(A，k)，对此式两边取自然对数，有lny=θln A+(1－θ)lnk，等式两边再对时间t求导，可得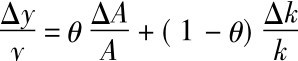。从此处可以得出新的认识:引入技术进步因素后，k的增长率为零时仍可以有人均产出y的增长，y的增长率取决于技术进步A的速率g。

(5)引入技术进步因素后，稳态下的总产出的增长速度取决于(g+n)。因为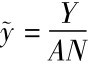，对此式两边取自然对数，并对时间t求导，有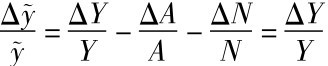－(g+n)，可得引入技术进步因素后，稳态条件下有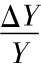=g+n。

表9－5说明了考虑技术进步情况下，新古典增长模型在稳态时，4个重要变量的增长率。

表9－5 具有技术进步的新古典增长模型中的稳态增长率

综上所述，可以得出新古典经济增长理论的主要观点: ①稳态中的总产出增长率是外生的，不考虑技术进步时，它等于人口增长率n; 考虑技术进步时，它等于g+n; 而独立于储蓄率s。②虽然储蓄率增加不影响稳态时总产出增长率，但通过提高资本－劳动比率可以提高稳态的收入水平。③稳态中的人均产出增长率是由外生的技术进步率决定的。④趋同是新古典经济增长理论最后的总判断，如果两国人口增长率、储蓄率和生产函数相同，它们最终将达到相同的人均收入水平，因此穷国是因为资本少才穷，但如果它们与富国的储蓄率一样，并有机会得到同样的技术，它们最终会赶上富国。

(三)黄金分割率

我们已经知道，新古典经济增长理论中，不考虑技术进步时，人均产出y的增长取决于人均资本k的增长; 稳态增长指的是人均资本k、人均产出y不增长而总产出Y随n的增长而增长的一种增长状态。但是，是否可以因此认为k值越大y值的增长就会越好? 推进y增长的目的我们不能忘记: 使人均消费c最大化。从经济稳态增长的图形(图9－7)可以读出，横轴表示稳态时的人均资本，纵轴表示与稳态相对应的人均产出、人均储蓄和人均消费。如果储蓄率s的取值不同，sy=(n+δ)k可以有多个稳态点。而不同的稳态点对应着不同的人均资本ki，代表着不同的人均储蓄水平，不同的人均储蓄水平的背后是不同的人均消费水平(y－s=c)。过高的储蓄率s导致低的人均消费c，而过低的储蓄率s，人均产出y低，人均消费c也就低。因为f(k)代表人均产出曲线，nk或者(n+δ)k代表维持简单再生产的曲线，f(k) －nk则代表着人均消费水平。例如T，M，X，Q四个点的人均消费水平，按照“人均消费=人均收入－人均储蓄”，即c=y－sy，马上可以算出分别为TT'，MM'， XX'，QQ'，显然不相等。提高人均消费水平是一个国家经济增长的根本目的。因此，我们现在需要找到人均消费水平最大化的人均资本点——人均资本k的选择首先是为了y－sy部分的最大化，而不是只是为了y的增长。也就是说，现在我们要找出sy曲线与nk直线相交时使f(k) －nk部分最大化的交点。美国著名经济学家埃德蒙·费尔普斯给出了明确的答案: 存在一个储蓄率水平s*，使得人均消费c*取最大值。假定不存在折旧，使人均消费水平最大化的交点就是f(k) －nk函数一阶导数为零的点。他的答案被称之为资本积累的黄金分割率。[7]这个储蓄率下使消费最大化的稳定状态值k*被称为资本的黄金率水平。

假定不存在折旧，则(n+δ)k就变为nk，稳态条件就变为:

sy=nk

稳态时，人均消费c就是人均收入与人均储蓄之差，即: c=y－sy，又由于sy=nk，y=f(k)，故可得到: c=f(k) －nk

人均消费c最大化的一阶条件是f'(k) －(nk)'=0，即:

f'(k) =n

上式就是黄金分割率表达式，其含义为: 要想使得稳态人均消费最大化，稳态人均资本量的选择就应该使资本的边际产品等于劳动的增长率。

图9－7 经济增长的黄金分割率

还可以用图9－7表示人均消费最大化时的人均资本量的选择。图中，稳态时的人均消费就是人均收入曲线y与直线nk之间的垂直距离。最大的人均消费量出现在人均资本等于k*的时候。因为在人均资本等于k*的时候，在k*点，y曲线切线的斜率正好等于n，即这条切线与直线nk平行。这种情况下，人均收入曲线y与直线nk之间的垂直距离M'M最大，即人均消费最大，M'M表示的人均消费量大于人均资本分别等于ˉk，k2时的消费T'T，X'X。T'T，X'X之所以小于M'M，是因为人均资本为ˉk，k2时所作的曲线y的切线都不与直线nk平行。这一结论与f'(k) =n式的意思完全相同。

从黄金分割率可知，稳态时，如果人均资本量多于黄金分割的水平，则需要通过消费掉一部分资本使人均资本减少到黄金分割的水平，这就能够提高人均消费水平。反之，人均资本量少于黄金分割的水平，则需要减少消费、增加储蓄，再通过储蓄转化为资本，使人均资本增加到黄金分割的水平。当然，经济运行在当期是否一定要达到稳态水平，取决于决策者对不同时期或者不同代际福利安排的取舍。

三、内生增长模型

新古典经济增长理论因其对于现实较强的解释力与精致的数学推导，掀起了经济增长理论的第二次革命，在20世纪60到80年代占据经济增长理论的主流地位，新古典增长理论模型有两个核心假设: 技术外生、规模收益不变且要素的边际收益递减。但随着人们对经济问题认识的深入和经济形势的发展，认为这两个假设都不符合现实，这一模型逐渐暴露出一些不足:

(1)这一模型只是说明了一个经济的储蓄率决定其资本存量的规模，从而决定其人均产出水平，但储蓄本身并不能产生经济的持续增长; 人口增长率的变化会影响经济的总产出变化、会影响稳态的人均资本k*发生变化进而影响人均产出y发生变化、会影响我们决定稳态黄金率资本水平标准，但它是外生变量，也不是人均产出持续增长的根本解释。当经济处于稳态时，经济增长只源自于技术进步。但技术进步又来自于哪里? 在新古典增长理论中只是一个假设，只是一个外生变量，并未加以解释。长期中人均产出的增长取决于模型未能解释的“假设增长”的技术进步，这是一个难以令人满意的理论解释。

(2)在新古典增长模型中，由于要素的边际收益递减规律，经济总量增长表现为收敛性，即按照时间路径将最终到达某种稳定状态。假定人均投资收益率和人均产出率是人均资本存量的递减函数，随着时间推移，各国工资率和资本产出比将会趋同。这是与一些国家经济增长的某些现实数据不符合的预测。

(3)由于把技术进步等作为外生因素来解释经济增长，因此，当要素收益出现递减时，经济将出现“沉闷和悲观的经济增长”的现象，如果不存在外生的技术变化，经济就会收敛于一个人均水平不变的稳定状态。这样，新古典增长理论就会面临一个令人不快的结果:除非有正的人口增长率或外生给定的技术变化，否则，长期中一国经济就会进入零增长，而这与之后观察到的事实也不尽符合。另外，根据该模型得出的观点，落后国家的经济增长要快于发达国家，因为落后国家的人均资本水平较低，单位资本的回报率比较高，但随后各国经济发展的实际情况表明，有些落后国家的增长速度反而低于发达国家的增长速度，落后国家与发达国家之间的差距有拉大的趋势。正是在这种情况下，20世纪80年代以来，以罗默和罗伯特·卢卡斯为代表的一批经济学家在反思新古典增长理论的基础上，逐渐形成了超越新古典增长模型的新增长理论，即内生增长理论。

内生增长理论试图避免新古典增长理论关于长期经济增长完全是由理论本身的外生因素决定的缺陷，修订了要素的边际生产力递减假设，提出一国的长期增长是由一系列内生变量决定的，并用内生技术进步和规模收益不变甚至增长来说明各国经济如何增长，将技术进步等要素内生化，得到因技术进步的存在要素收益会递增而长期增长率是正的结论，故称内生增长理论。

内生增长理论发展分为两个阶段。在20世纪80年代第一个阶段，主要在完全竞争假设下考察长期增长率的决定。20世纪90年代开始，主要在垄断竞争假设下研究经济增长问题，提出了一些新的内生增长模型。主要的内生增长模型大致分为以下几类:

(一)AK模型

这是放弃资本收益递减规律并能够导致内生增长的模型。

假设生产函数为Y=AK，Y是总产出，K是总资本存量; s为储蓄率，δ为折旧率，s与δ均为外生变量。A为衡量单位资本所生产的产出量，为反映技术水平的正的常数; 该函数说明资本积累导致资本边际产品不是趋近于零，而是等于一个正数A，不存在资本边际收益递减。

于是资本积累可描述为

ΔK=s Y－δK

令Y1=AK1，Y2=AK2，则有ΔY=Y2－Y1=A(K2－K1) =A·ΔK，

这一模型表明，决定产出增长率ΔY/Y的是s A－δ。只要s A＞δ，即使没有外生技术进步的假设，资本积累也足以保证经济沿着平稳的路径一直增长。于是可以对经济增长重新说明: 新古典增长理论中，储蓄引致了经济的暂时增长，但资本边际收益递减最终使经济达到增长只取决于外生技术进步的稳定状态; 而在内生增长的AK模型推导中，放弃了资本边际收益递减的假设，经济的增长主要取决于储蓄率s与技术水平A; 储蓄与投资会引起经济持续增长。放弃这一假设合理吗?

我们知道，新古典经济增长模型的推导中假定资本的边际收益是递减的，因此y曲线与对应的储蓄线sy向右上方弯曲逐渐变得平直，必需的投资线(n+δ)k与储蓄线sy肯定相交(见图9－2)。现在，内生增长理论中放弃资本边际收益递减的假设。于是，y与sy由曲线变成了直线，储蓄sy总是大于必需的投资(n+δ)k，储蓄率越高，sy－(n+δ)k越大，人均资本k的增长从而经济增长也就越快。我们可以看到与图9－2完全不同的图9－8。放弃这一假设后经济是否同样持续增长取决于人们如何认识Y=AK中的资本K。传统意义下的K是指固定资本。如果是这样来认识K，在有形损耗与无形损耗的驱动下，资本边际收益递减的假设当然合理; 可是，内生增长理论意义下的K不仅仅指实物资本，还包括知识资本，比如人力资本投资和研究与开发投资，而实际上历史表明知识资本是存在边际报酬递增的。如果这样来认识K，内生增长理论放弃资本边际收益递减的假设就是合理的，对于经济持续增长的描述就成立; 在所有增长理论中对于经济持续增长的解释就更合理。在中国经济当前的增长主要还是依靠投资的拉动、依靠出口和对外招商引资、内生动力不足的情况下，对于内生增长理论的讨论具有重要意义。

图9－8 内生经济增长模型

(二)外部性模型

外部性模型是既不放弃资本收益递减假定和完全竞争又能产生内生增长的经济增长模型，是以外部性和知识溢出为基础的增长模型。这类增长模型的基本特征是: 其一，技术进步、知识积累或人力资本积累是其他经济活动的副产品，因而不需要补偿并可维持完全竞争的分析框架; 其二，个别厂商的生产函数表现为不变规模收益，但就整个经济而言表现为规模收益递增; 其三，上述两个特征决定了这类模型具有不同于新古典增长理论的政策含义，即政府政策不仅具有水平效应，而且具有增长效应。根据外部性来源的不同，这类模型以“干中学”及知识溢出模型为代表。

“干中学”模型认为，一方面，企业在进行投资和生产的过程中会逐步积累起生产经验和更有效的生产知识，而这些经验与知识能够提高企业的生产效率; 另一方面，一个企业获得的生产经验和生产知识也能够通过产品销售、资本渗透与人事交流等形成溢出而被其他企业无偿地利用，从而使得其生产率也有所提高。因此，一个企业的总产出可以视为整个经济总投资的函数。也就是说，知识的创造是投资的“副产品”(即干中学)，知识的溢出导致了整个经济生产率的提高(即溢出效应)。可以通过对特定的生产函数做一些特点的假设来推导说明“干中学”及知识溢出是经济内生增长的源泉。

假定: ①代表性厂商i的生产函数为Yi=F(ki，K，xi)，其中: ki是该厂商的知识水平，xi是该厂商的其他有形投入(例如物质资本和原始劳动等)，K代表整个经济的总知识存量; ②对于个别厂商的自身投入xi和ki而言，该生产函数表现出不变规模收益，满足新古典生产函数的假定。

根据以上假定来讨论生产函数Yi=F(ki，K，xi)对于代表性厂商和整个经济的含义: 首先，对于代表性厂商而言，总知识水平K为给定的变量，因此，生产函数表现为不变规模收益; 其次，对整个经济(假定它由N个同质的厂商组成)而言，总知识水平K不再是给定的常数而是影响总产出的一个自变量，所以，对于任何常数λ＞1有F(λki，λK，λxi) ＞F(λki，K，λxi)=λF(ki，K，xi)，因此，对于生产函数Y=F(ki，K，xi)当考虑K为变量时表现为规模收益递增，所以整个经济的生产函数NY=NF(ki，K，xi) =NF(ki，K，xi)也具有规模收益递增的性质。在这里，总知识水平K成为外部性的来源。此外，模型还假定ki的增长率取决于ki的水平和投资数额(产出中没有用于消费的部分)。这样，通过知识积累的“副产品”性质和知识存量的外部性得到了内生增长。

(三)人力资本模型

人力资本不同于物质资本，它是指体现在劳动者身上的可用于生产产品或提供各种服务的智力、技能以及知识的总和，必须通过教育和培训等的成本才能形成。模型假定: 其一，人力资本的增长率是人们用于积累人力资本的时间比例的线性函数(这与纯粹的“干中学”模型有所不同)，从而引入了人力资本生产部门。其二，投资者的人力资本具有两种效应: 一种是人力资本的内部效应，即人力资本的增加会使得投资者本身生产率的提高; 另一种是人力资本的外部性，因为人力资本可以无成本的传递，所以人力资本的增加不仅提高了投资者本身生产率，还提高了整个社会的生产率(每一经济个体在进行决策时不考虑这部分影响)，这种外部性就是该模型能够产生递增规模收益的基础。

在引入了人力资本之后，根据以上的假定，可以将生产函数设为: y=Akα(uh)1－α，其中k为物质资本; u为工人用于生产的时间，将工人可用时间正规化为1，则有0＜u＜1; h为人力资本。因此，从生产函数可以看出，只要物质资本k和人力资本u同比例增长，线性齐次函数依然可以使得总资本的报酬率不变，即考虑了人力资本的生产函数能使经济持续地内生增长。但人力资本的增加来源于何处呢? 一般认为有两种途径: 一是通过教育提高经济活动中个体的知识和技能，从而提高劳动生产率; 二是通过生产和实践中的经验积累，即“干中学”模型。所以说“干中学”模型其实是人力资本模型的一个特例。

(四)研究与开发模型

即R＆D(research and development)模型。外部性模型通过引入知识积累或人力资本积累，并借助于溢出效应得到了内生增长。R＆D模型则认为技术进步或创新是厂商进行有意识的、旨在获取垄断收益的活动的结果，正是这种内生的技术进步打破了边际报酬递减，实现了经济的持续内生增长。该模型认为技术具有不同于传统经济物品的两大特点: 非竞争性的和部分排他性。因而完全竞争的假定被放弃，而使用具有市场势力的垄断竞争模型进行分析。非竞争性意味着生产表现为规模收益递增，这点与外部性模型是一样的; 部分排他性则为从事R＆D活动的厂商提供了激励。所以R＆D与外部性模型的不同点就在于R＆D模型把技术的外部性与垄断结合起来，因此就没有再考虑技术的外溢。以R＆D为基础的增长模型主要有两类: 一类是将技术进步理解为产品种类的增加(例如新行业的开辟)，一类是将技术进步理解为产品质量的改进(例如同类产品的升级换代)。这两类模型的主要区别在于后者引入了熊彼特的“创造性破坏”概念，即新产品的出现往往意味着旧产品的被淘汰。

[1] 新古典增长模型又被称为外生经济增长模型，是在新古典经济学框架内的经济增长模型，是理解发达国家经济增长的基本工具。由美国经济学家罗伯特·索罗(Robert M．Solow)提出，他以此为基础的研究获1987年诺贝尔经济学奖。

[2] 这里假设社会只存在一种类型的资本品，以简化讨论。

[3]为简化讨论，将y定义为连续的关于时间的函数。上述推导过程中用到了复合函数的导数。当y(t) =lnx(t)，对函数两边求导的结果为: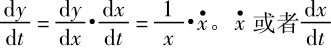，表示单位时间(通常指一年)内x的增量，因此，某个变量的对数关于时间的导数就是这个变量的增长率。

[4]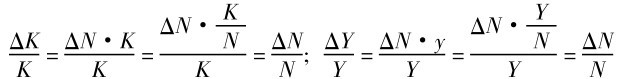

[5] 在生产函数Y=F(A，N，K)中，AN表示劳动强化型技术进步，AK表示资本强化型技术进步，如果A位于括号外面表示技术进步在劳动与资本的偏向中处于中性，又称之为希克斯中性。劳动强化型技术进步才能推出式(9．20)及其后面的结论。

[6] 由前述假定条件可知，以C－D生产函数为背景、具有劳动加强型技术进步的生产函数为: Y=F(AN，K) =(AN)θK1－θ⇒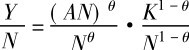⇔y=Aθk1－θ，其中0＜θ＜1。

[7] 费尔普斯因此项研究获得2006年诺贝尔经济学奖。