不完全信息下的多要素投入

在上述分析中，我们可以看到，佃农只有一个决策变量，即努力程度e，如果佃农可以控制一个以上的变量(要素的投入不止一项时)，那么分成制契约是否会反映这一点呢?伯瑞弗曼和斯蒂格里兹(Bravermanand Stiglitz，1982)考察了不完全信息下多要素投入的风险分担问题。

假设佃农的收入为

式中:x是指化肥的投入;p为价格;β为佃农承担化肥成本的比例。地主的预期利润可以表示为

佃农的最优规划可以表示为maxE［U(Y)－e］，那么根据这个最优规划，我们可以确定佃农的投入e和x，它们分别是两个隐函数e(α，β)和x(α，β)。地主在两个约束条件(PC)和(ICC)下选择分成合同的条件，(PC)由EU(α，β)≥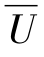给出，(ICC)由上面两个隐函数给出。因此，α可以表示为β的函数。那么，地主的利润就可以写为

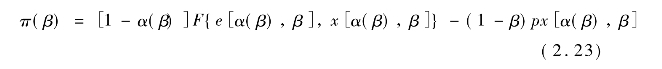
(1)当α≠β时，若化肥使用量随劳动的边际产出增加而增加，地主可能会通过降低β(佃农分担化肥成本)而提高α(佃农的收入分成)，从而改变佃农所面对的风险。

(2)当α=β时，由于佃农是风险厌恶的，仍然会少施化肥，而地主是风险中性的，他(她)仍会通过降低β来鼓励佃农多用化肥。

在以上的分析中，涉及一个“等比例”分成的问题(α=β)，一般文献的假设是，如果地主可以以与产出比例相同的比例分担化肥成本，化肥的配置会达到最优水平。但事实上，如果引入信息不对称和不确定性，这个“等比例”是不存在的，也就是在上述问题的一般解中，α≠β。关于“等比例”分成规则在世界许多地方占主导地位，速水佑次郎和大塚(Hayamiand Otsuka，1993)认为，其原因是非劳动力投入可能是由地主决定并执行的。

如果我们对以上模型作进一步的分析，我们会发现，一旦佃农的化肥投入量x是无法观测的，那么地主就不会对成本进行分担。巴德汉和辛吉(Bardhanand Singh，1987)从另外一个角度考察了这个问题。假设地主选择购买化肥量z，佃农可能不会完全使用(卖掉一部分，或者在其他地方使用一部分)。那么，佃农的收入和地主的预期利润分别为

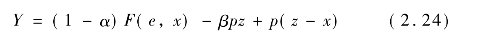
如果给定α，β和z，佃农选定其努力程度e和化肥投入x，那么地主会考虑佃农的行为，从而决定α，β和z。我们可以将(2．24)，(2．25)两式改写为

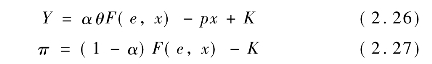
其中，K=(1－β)pz，可看作是佃农的固定成本，那么佃农使用化肥的边际成本为p，此时，地主不能操纵佃农使用化肥的边际成本，而由佃农自己决定使用多少化肥，在这种情况下，可以认为是一种成本分摊而不是边际成本分摊。