指标权重确定的方法

6.3.1　指标权重确定的方法

评价指标权重确定的方法主要有主成分分析法和层次分析法。

在计算某地区产业竞争力的多项评价指标的综合值前，需要确定指标权重。权重是对各个指标在指标总体中的重要程度的度量。因此，权重确定的是否科学、合理直接影响着评价的准确性，是评价过程中的一个极其重要的因素。

那么，应如何确定权重呢?目前，前面所说的个人判断法、专家会议法和德尔菲法都是较为常用的分析方法，但都有主观性较强等不足。为了克服上述方法的缺陷，我们主要采用主成分分析和层次分析方法。

具体而言，我们设计的产业国际竞争力评价指标体系中，由于一级、二级指标相对于三级指标而言，其权重对竞争力评价结果有较大的影响，因此我们运用主成分分析法和AHP法确定各指标的权重，对于三级指标，则采用Deilph法确定各指标权重。

一、 主成分分析法

主成分分析法的基本步骤是：

（1） 样本数据标准化变换。设样本数据矩阵为X＝（x_ij）_m*n，即n个指标m个样本。标准化数据矩阵为Y＝（y_ij）_m*n，标准化变换公式为：

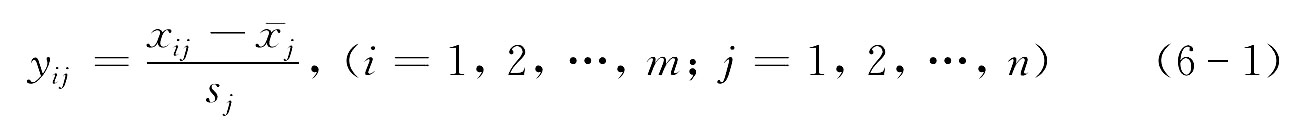
其中，

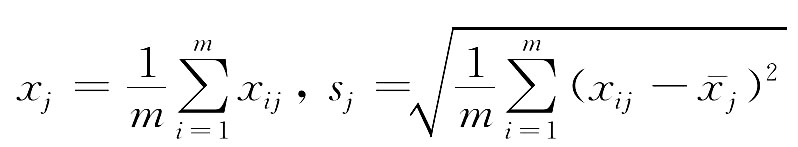
经过标准化变换后，各样本的均值和方差分别为0、1。

（2） 写出样本相关矩阵。设样本相关矩阵R＝（r_η）_m×n，相关系数

并且有r_ij＝r_ji， r_ii＝1，所以R是对称矩阵，主对角线上元素均为1。

（3） 计算相关矩阵R的特征值和对应的特征向量。特征方程|R－λI|＝0。解出n个特征值：

λ₁≥λ₂≥…≥λ_n， （i＝1， 2， Λ， p）

由齐次线性方程组|R－λI|L＝0，解出对应的特征向量：

L_j＝（l_1j， l_2j，…， l_nj）^T， （j＝1， 2，…， n）

（4） 按累计贡献率准则提取主成分。计算各主成分的贡献率：

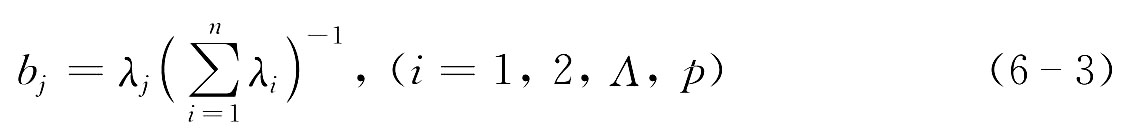
并按累积贡献率准则，即以累积贡献率：

为准则，提取k个主成分

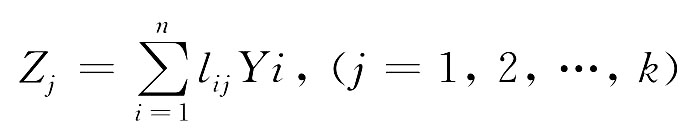
式中，Z_j＝（z_1j， z_2j， …， z_nj）^T， Y_i＝（y_it， y_2t， …， y_mt）^T，这表示第j个主成分是标准化指标样本的线性组合，其系数式特征值λ_j，对应的特征量L_j的分量。

（5） 分析主成分的经济意义，用主成分进行综合评价。

综合评价值根据具体情况，可以取第一主成分，也可以用k个主成分的加权平均值，权数取各主成分的贡献率b_j，即综合评价值为：

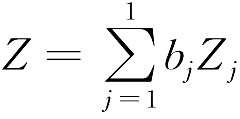
二、 层次分析法

层次分析法的主要步骤如下：

（1） 确定目标A和评价因素集U。

（2） 构造判断矩阵。

以A表示目标，u_i表示评价因素，u_i∈ U， （i＝1， 2， 3， …， n）。u_ij表示u_i对u_j相对重要性数值，（j＝1， 2， 3， …， n）， u_ij的取值以表6.1进行。

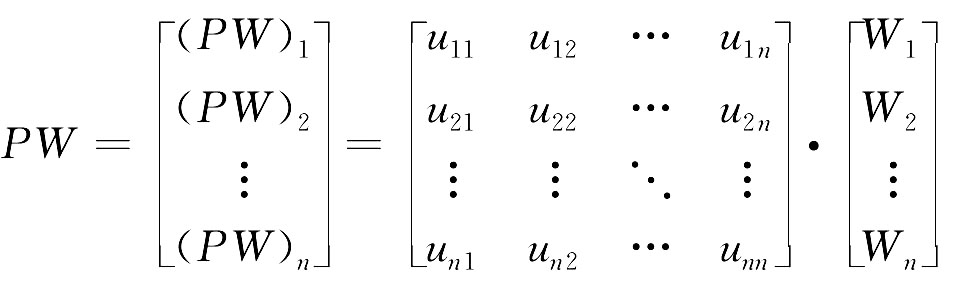
根据上述各符号的意义得到判断矩阵P：

称之为A—U判断矩阵。

（3） 计算重要性排序。根据A—U矩阵，求出最大特征根所对应的特征向量。所求特征向量就是各评价因素重要性排序，即权数分配。

特征向量具体求法为：

计算判断矩阵每一行元素的乘积M_i：

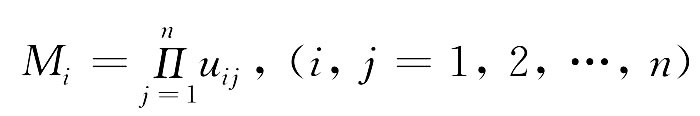
计算M_i的n次方根：

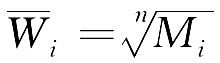
对向量W＝［W₁， W₂， …， W_n］^T作归一化处理，即：

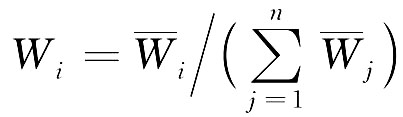
则W＝（W₁， W₂， …， W_n）^T即为所求特征向量。

计算判断矩阵的最大特征根λ_max：

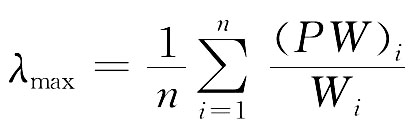
式中（PW）_I表示向量PW的第i个元素。

（4） 一致性检验。以上得到的特征向量即为所求权数，权数的分配合理与否，需要对判断矩阵进行一致性检验，检验使用的公式为：

CR＝CI/RI

其中： CR称为判断矩阵的随机一致性比率；

CI为判断矩阵的一般一致性指标，它由下式给出：

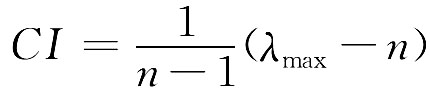
RI为判断矩阵的平均随机一致性指标，对于1—9阶判断矩阵，RI值列于表6.2。

当CR＜0.10，或者CI＝0.00时，即认为判断矩阵具有满意的一致性，说明权数分配是合理的；否则，就要调整判断矩阵，直到取得具有满意的一致性为止。

利用层次分析法计算评价指标的权数分配可以较大幅度地减少主观因素。如果人的主观判断偏离了客观实际，则CR的值便显示了这种差别，以便对判断矩阵作出调整，直到接近客观实际为止，所以这种方法较为适用。

应该指出，由于市场环境和人们对事物的认识在不断变化，因此，评价指标的权重也应当随着客观情况的变化和人们认识的变化，以及经验的总结和积累进行适时的调整，以体现事物发展的要求。