层次分析法(Analytic Hierarchy Process,AHP)是由美国著名运筹学家萨蒂(T.L.Saaty)教授于20世纪70年代提出的一种系统分析方法。这种方法把一个复杂的问题按属性的逻辑关系逐层分解,形成一个层次结构来加以分析,并在逐层分解的基础上加以综合,给出复杂问题的求解结果。它是用一定标度把人的主观判断进行客观量化,将定性问题进行半定量分析的一种简单而又实用的多准则评价决策方法。AHP强调决策者直觉判断的重要性和决策过程中方案比较的一致性,目前已在各个领域获得广泛的应用。
(1)层次分析法基本原理
AHP算法是一种有效处理那些难以抽象为解析形式的数学模型问题(即非结构化问题),或难以完全用定量方法来分析的复杂问题的手段,它为实际应用中的多规则决策问题提供了有力的量化支持。其基本原理可以归结为:通过分析复杂系统所包含的因素及其相互关系,将系统分解为不同的组成要素,并将这些要素划归不同层次,从而形成多层次的分析结构模型。根据指标的层次结构特点,将每一层次的各要素相对于其上一层次各要素进行两两比较判断,得到其相对重要程度的比较标度,建立判断矩阵。通过计算判断矩阵的最大特征根及其相对应的特征向量,进行层次单排序,得到各层要素相对上层某要素而言的重要性次序,建立相对权重向量。最后,自上而下地用上一层次各要素的组合权重为权数,对本层次各要素的相对权重向量进行加权求和,进行层次总排序,得出各层次要素关于系统总体目标的组合权重,从而根据最终权重的大小进行方案排序,为选择最佳方案提供决策依据。
(2)层次分析法一般步骤
①构造判断矩阵。一个因素被分解为若干个与之相关的下层因素,各下层因素对该因素的作用大小不同,一般称为权重向量W。通过各因素的重要程度两两比较,构成一个判断矩阵。所谓判断矩阵,是以矩阵的形式来表述每一层次中各要素针对其上层某要素而言的相对重要程度。建立判断矩阵是层次分析法中最关键的一步。
针对上层要素Ui,假设A1,A2,…,An是n个与Ui相关联的下层要素,根据分析A层各要素间针对Ui而言的相对重要程度,可以构造一个n×n阶的判断矩阵,如表9-4所示。
表9-4 n×n阶判断矩阵
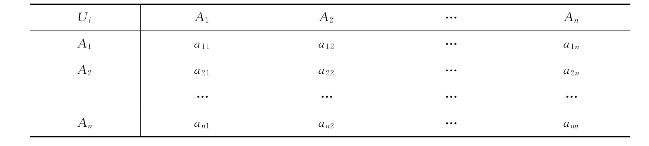
其中,akj表示针对Ui而言,要素Ak对Aj的相对重要程度,即重要性的比较标度。相对重要性的量值用萨蒂建议的1—9标度法来表示,如表9-5所示。
表9-5 1—9标度法的含义
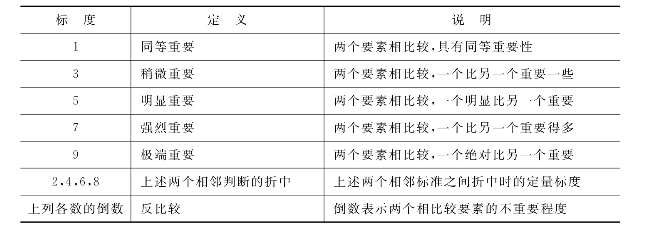
判断矩阵使决策者的思维数字化,因此在应用层次分析法时,保持判断思维的一致性非常重要。衡量判断矩阵质量优劣的办法是检验定性思维是否具有一致性,当判断矩阵满足一致性条件时,判断矩阵的元素aij就是各个因素权重的比值,即aij=wi/wj,判断矩阵有唯一非零特征值n(也是最大特征值),这时,n所对应的特征向量就是各元素的权重系数。
②进行层次排序。一般求解判断矩阵不需要太高的精度,所求的特征值和特征向量也不是严格意义上的解析解。实际上,当矩阵有较高阶数或者说比较因素较多时,特征值的解析解是很难求出来的。一般来说,有两种近似方法可以求解最大特征值:一种是方根法,一种是求和法。此处采用方根法来求解。
第一,计算n阶判断矩阵每一行各元素的乘积Mk:
第二,计算Mk的n次方根珨Mk:
![]()
第三,规范化处理(归一化处理)得特征值Wk:
从而得到特征向量ω=(ω1,ω2,…,ωn)T,就是所求相对权重向量。
第四,近似计算最大特征根λmax:
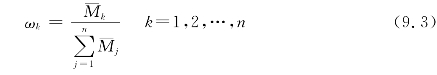

③一致性检验。由于人们认识的片面性,在进行主观评价时,所建立的判断矩阵不可能表现出完全一致性。这就需要对所建立的判断矩阵进行一致性检验,以防止对各要素重要性的判断出现矛盾现象。只有通过一致性检验的判断矩阵才可用于层次排序。
引入判断矩阵的一致性指标(Consistency Index),记为C.I.,计算式如下:
![]()
C.I.值越大,表明判断矩阵偏离完全一致性的程度越大;C.I.值越小(越接近于0),表明判断矩阵的一致性越好。
对于不同阶的判断矩阵,人们判断的一致误差不同,其C.I.值的要求也不同。为度量不同阶判断矩阵是否具有满意的一致性,再引入判断矩阵的平均随机一致性指标(Random Index),记为R.I。是一个系数,对应不同阶次的数值如表9-6所示。
表9-6 平均随机一致性指标

对于一阶、二阶矩阵,判断矩阵是完全一致的,不必计算一致性指标。当n≥3时,判断矩阵的一致性指标C.I.与同阶平均随机一致性指标R.I.之比称为随机一致性比值(Consistency Ratio),记作C.R.,即
![]()
当C.R.<0.1时,即认为判断矩阵具有满意的一致性;C.R.≥0.1时,则认为判断矩阵不一致,应作适当调整,使其满足C.R.<0.1,从而具有满意的一致性。
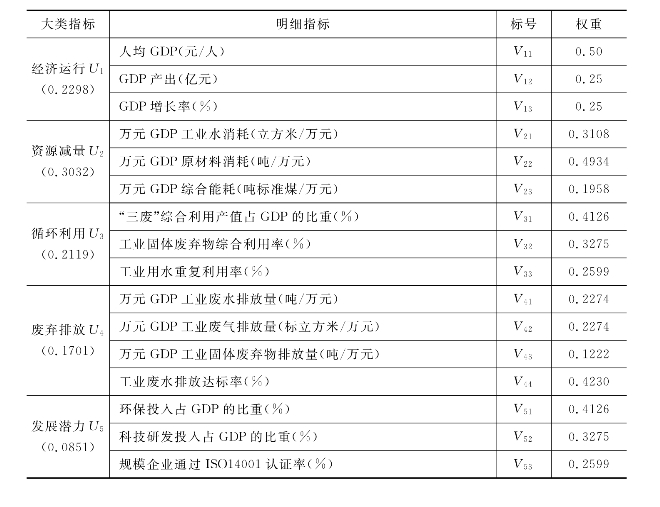
因此,经过对专家访谈意见的汇总整理,采用“1—9标度法”,得到大类指标的判断矩阵;运用方根法求解,确定区域循环经济评价指标的相对权重,具体结果如表9-7所示。
表9-7 区域循环经济评价指标权重
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















