行业特征与制造业产业升级

本节将在Leung　＆Yuen（2010）模型的基础上，分析人民币汇率对中国制造业技术进步的影响。本节在理论分析中引入资本调整成本的影响，考察在存在资本调整成本的情况下汇率对制造业技术进步的影响机制；在经验分析中测算制造业各行业的实际汇率，分析不同行业实际汇率的差异，从而进一步研究汇率调整对制造业各行业技术进步的非对称性影响。

7．3．1　理论模型

为了便于分析，本节作如下假设。第一，存在一个典型的出口产品制造商，该厂商投入资本和劳动，产品用于出口^[2]。第二，本文根据Bernstein　＆Mamuneas（2005）及Lee　＆Kim（2006）的研究，将资本的用途分为技术更新和生产制造，厂商通过调整技术更新投入、生产制造投入和劳动投入量，实现利润最大化。技术更新投入主要用于研发、引进先进的机器设备，生产制造投入用于购买直接用于生产的原材料。厂商技术进步反映了厂商可以用更少的投入生产更多的产出，而不仅仅指劳动生产率的提高。第三，厂商改变技术更新资本投入和生产制造资本投入会产生资本调整成本。第四，假设该国采用有管理的浮动汇率制度，汇率在很大程度上受政府干预，为模型的外生变量。汇率以直接标价法表示，出口商品以外币标价，厂商无法影响国际市场价格。此外，本节将产品的国内价格标准化为1。

该厂商的实际利润等于出口的实际总收入减去资本和劳动的实际成本以及资本调整成本，本节在Leung　＆Yuen（2010）方法的基础上加入资本调整成本，将厂商的目标函数表示为：

其中，Πt，Yt，Kt，Lt和CACt分别表示厂商利润、产量、资本投入、劳动总量和资本调整成本；qt为以直接标价法表示的汇率；r和w为实际利率和实际工资率，它们也反映了一国经济和金融市场发展程度。我们假定这些参数外生，以考察特定的经济发展阶段汇率调整对制造业行业技术进步的影响。由于国内价格标准化为1，国际市场价格（PF，t）实际上等于该产品的国内外比价，（7．23）式中名义汇率与国际市场相对价格的乘积（qt·PF，t）等于行业的实际汇率（exrt）。由（7．23）式可见，在其他因素不变的情况下，本币升值将减少出口收入的本币价值，从而减少厂商的实际利润。

假定厂商具有柯布-道格拉斯生产函数，即：

其中，At表示该厂商的技术水平；KM，t表示该厂商的生产制造资本投入量；α和β分别表示用于生产制造的资本和劳动投入对产出的贡献率。

根据前提假设和现有研究，厂商的技术进步的速度受技术更新投入和用于技术更新的人力资本投入的影响（Jones，1995；Hornstein　＆Peled，1998），技术函数可以表示为：

其中，A0为初始技术水平；KR，t表示该厂商用于技术更新的资本投入量；参数ξ反映了研发效率，且ξ＞α，技术更新资本对产出的贡献比生产制造资本大；LR，t为用于技术更新的人力资本投入；λ为研发人力资本投入对厂商技术进步的影响系数，且ξ和λ均大于0。

对于任何厂商来说，其当年的研发资本存量（KR，t）等于原有研发资本存量（KR，0）加上当年研发投资（IR，t），即：

根据Bernstein　＆Mamuneas（2005）及Lee　＆Kim（2006）的研究，生产制造资本投入（KM，t）和技术更新投入（KR，t）之和为厂商的总资本（Kt），即：

在一国经济金融发展水平不高的情况下，厂商往往面临资本硬约束。此时，由于资本总量一定，用于技术更新的资本投入越多，可用于生产制造的资本就越少。

对于厂商来说，由于资本投入会形成沉淀成本，因此，改变生产制造资本和技术更新资本的比重、调整资本结构就会产生资本调整成本。一般来说，资本调整的规模越大，调整成本就越高。多数研究认为，资本调整成本比劳动调整成本大得多（Hall，2004），因此，本节忽略劳动调整成本。同时，对于资本密集度较高的厂商来说，厂商对资本的依赖更大，改变生产制造资本投入会极大地影响产出，其资本调整成本更高（Chakrabarti，2009）。在总投资量一定的情况下，如果厂商新增技术更新投资，就必须减少生产制造投资。因此，厂商的资本调整成本可以表示为资本—劳动比率和新增技术更新投资的函数，即：

其中，σ为参数。

由以上各式，可以得到厂商利润最大化时的一阶欧拉条件：

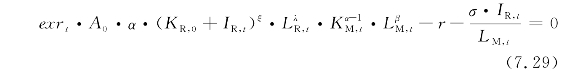
（7．29）式表明，当厂商的生产制造资本投入等于其边际成本时，厂商生产达到最优水平，可以实现利润最大化。显然，由于存在资本调整成本，只有当生产制造资本投入的边际产出更高时，厂商才会增加生产制造投资，否则就会增加技术更新资本投入。

由（7．29）式，假定其他因素不变，可以得到利润最大化时厂商的最优技术更新资本投入与汇率之间的关系，即：

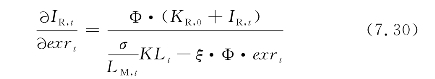
其中，Φ＝A0·α·（KR，0＋IR，t）ξ－1·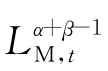，且KLt＝Kt／Lt，为厂商的资本-劳动比率。一般来说，对于资本密集型行业来说，KLt较大，因此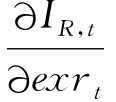大于0，本币实际汇率升值，exrt下降，技术更新投资就会减少，厂商减少技术更新资本；在劳动密集型行业中，KLt较小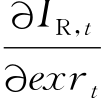，就会小于0，本币实际汇率升值，技术更新资本投入上升。这是因为，当本币实际汇率升值时，厂商出口减少，为了维持利润最大化，厂商有两个选择：一是减少生产制造资本投入，增加技术更新投入，通过技术更新提升利润；二是压缩技术更新投入，通过增加生产制造资本投入以扩大生产规模，增加利润。对于资本—劳动比率高的行业，也就是资本密集型行业来说，由于存在资本调整成本，减少生产制造资本投入、增加技术更新资本投入会带来较高的资本调整成本，不利于利润的增加。相反，对于劳动密集型行业来说，资本调整成本相对较低，增加技术更新投入对利润的提升作用更大。因此，在本币实际汇率升值时，资本—劳动比率高的厂商会减少技术更新投入。

由（7．25）式和（7．30）式，可以得到厂商技术进步与行业实际汇率之间的关系：

由（7．31）式可见，汇率调整能够影响制造业厂商技术进步，但其影响是复杂的，具有非对称性特征。行业的资本-劳动比率不同，行业实际汇率对各行业技术更新投入和技术进步的影响也将存在很大差异。对于资本密集型行业来说，资本-劳动比率（KLt）较高，厂商对生产制造资本的依赖更大。由于生产制造资本大多具有专用性（specificity）特征，减少生产制造投入、增加技术更新投入带来的资本调整成本过高，厂商无法在短期内迅速地实现资本投入结构的调整。因此，行业实际汇率升值后资本密集型行业中的厂商难以立即增加技术更新投入，技术进步受到的影响较为有限。但是，在劳动密集型行业中，资本-劳动比率（KLt）较低，厂商对生产制造资本的依赖度相对较低，资本调整成本不大，行业实际汇率升值后厂商可以立即增加技术更新投入，从而促进行业技术进步。

7．3．2　方法与数据

在理论分析的基础上，本节将运用经验分析方法研究分行业汇率对中国制造业行业全要素生产率的影响。

1．研究方法

本节首先测算制造业的行业实际汇率，再利用本章第一节中所描述的ODonnell（2010）的数据包络方法估算中国制造业行业2002～2010年的全要素生产率，最后利用面板数据模型分析行业实际汇率对制造业行业的影响，同时还将进行稳健性检验。

首先，我们根据Goldberg（2004）的方法，分两步计算行业实际汇率。第一步，先计算人民币对制造业行业主要贸易伙伴的实际汇率。实际汇率的计算公式为：

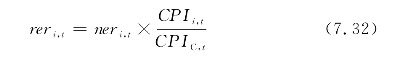
其中，rer和ner分别表示实际汇率和名义汇率，均以直接标价法表示；CPI为消费者价格指数，中外CPI均为以2001年为基期的年度同比数据；下标i和t分别表示第i个贸易伙伴和第t年，CPIC，t表示中国在第七年的消费者价格指数。第二步，再计算行业实际汇率。行业实际汇率等于以中国与各贸易伙伴国的贸易量为权重的加权平均实际汇率：

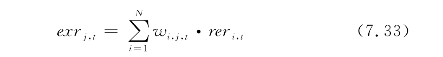
其中，exrj，t表示第j个行业在第t期的实际汇率；wi，j，t表示第j个行业在第t期与第i个贸易伙伴的贸易量在该行业总贸易量中所占权重。本节将根据世界贸易组织（WTO）统计的行业贸易指标计算权重。

其次，本节的理论模型分析了行业实际汇率对制造业行业技术进步的非对称性影响机制，考虑到（7．31）式中包含较多未知参数，无法直接运用经验分析方法进行估计，本节将构建简化的经验分析模型，考察资本—劳动比率在不同的行业中实际汇率对制造业行业技术进步的影响，验证理论分析的结论。本节利用面板数据模型分析行业实际汇率对制造业全要素生产率的影响，为了考察行业实际汇率对不同类型行业全要素生产率的影响，我们在利用全样本数据进行分析之后，还根据行业的平均资本—劳动比率指标对制造业行业进行分组，将行业平均资本—劳动比率高于全部行业平均水平的划为高比率组，低于平均水平的行业划为低比率组，研究行业实际汇率对分组指标的影响^[3]。本节经验分析中，同时运用最小二乘法（OLS）和广义矩（GMM）方法估计模型参数。由于本节的经验分析包含了全部28个制造业行业，且制造业行业全要素生产率可能存在行业截面差异和时间差异，我们在OLS方法中包含了截面—时间固定效应，利用White方法进行异方差调整，同时利用截面—时间固定效应F检验验证模型是否存在截面—时间固定效应。根据巴拉萨-萨缪尔森效应，技术变动会影响汇率，全要素生产率的变化也会影响汇率，用行业实际汇率作为自变量、以行业全要素生产率作为因变量可能会产生模型的内生性问题，降低模型估计结果的有效性。为了克服模型可能存在的内生性问题，我们将运用广义矩（GMM）方法估计模型参数。在广义矩方法中，我们根据Miguel等（2004）的方法，选择自变量的一阶和二阶滞后项作为工具变量。为了验证工具变量选择的有效性，我们再运用Sargent－Hansen检验的J统计量进行过度识别检验。Sargent－Hansen检验的原假设是模型不存在过度识别问题，工具变量选择有效，可以克服模型内生性问题。

由于全要素生产率是反映行业技术水平进步的动态指标，本节相对应地以行业实际汇率与上年的变化率作为行业汇率指标，反映行业实际汇率的变动。我们的基本模型如下：

其中，dlexrj，t＝ln（exrj，t）－ln（exrj，t－1），衡量行业实际汇率的变化率（当dlexrj，t＞0时，行业实际汇率贬值，而当dlexrj，t＜0时，行业实际汇率升值）；CONTj，t为一系列控制变量；μj，t为残差项。

第三，根据Aghion等（2009）、Benhima（2010）和Biatour等（2011）的研究，本节的控制变量包括研发活动、人力资本、市场竞争、国际贸易、财务状况、发展速度和行业中企业规模等。在控制变量的指标选择上，本节以研发投资占销售额比重反映研发活动，以劳动总量衡量人力资本^[4]，以行业中企业数量的倒数衡量市场竞争程度，以出口交货额占销售总量的比重衡量国际贸易的影响，以资产负债率和流动资产比率反映行业中的企业财务状况，以行业工业增加值的增长速度反映行业发展速度，以大中型企业比重反映企业规模。

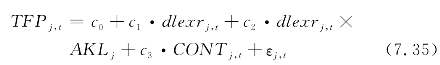
第四，本节参考Aghion等（2009）的交叉项方法，就行业实际汇率对全要素生产率的非对称性影响机制进行稳健性检验。在模型中增加行业平均资本-劳动比率和行业实际汇率的交叉项，验证行业实际汇率对全要素生产率的非对称性影响。稳健性检验的模型为：其中，AKLj为第j个行业的平均资本—劳动比率；εj，t为残差项。汇率对行业全要素生产率的综合影响系数为c1＋c2· AKLj，当c1和c2的符号相反时，说明行业实际汇率对全要素生产率具有非对称性影响，且其影响方向与行业的平均资本-劳动比率（AKLj）有关。同样，在稳健性检验中，我们也分别采用截面—时间固定效应面板数据模型和广义矩方法拟合（7．35）式。

2．数据说明

由于中国制造业行业从加入WTO后开始加速发展，本节在经验分析中选用2002～2010年中国28个制造业行业的工业增加值、劳动、工资、资产规模、工业品出厂价格、固定资产投资价格指数、各行业内国有企业总产值、外资企业总产值、流动资产比率、资产负债率、资本—劳动比率、2002～2010年人民币对美元、欧元、日元、英镑、新台币和港币的汇率，以及美国、欧元区、日本、英国、中国台湾和中国香港等经济体的消费者物价指数等数据。由于行业资产包括固定资产和流动资产，我们利用各行业固定资产和流动资产的构成比率，以及固定资产价格指数与原材料、燃料和动力购进价格指数构建加权资产价格指数，具体计算公式为：APA，t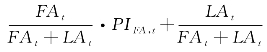＝·PILA，t。其中：APA，t，FAt，LAt， PIFA，t和PILA，t分别表示第t年加权平均资产价格指数、固定资产年平均余额、流动资产总额、固定资产价格指数和原材料、燃料和动力购进价格指数。在行业实际汇率计算过程中，根据世界贸易组织网站的统计，我们选择欧元区、美国、日本、英国、中国香港、中国台湾和韩国等7个最主要经济体作为制造业行业的主要贸易对象。所有数据选自《中国统计年鉴》、美国劳动统计网、欧洲中央银行网站、日本银行网站、韩国中央银行网站、世界贸易组织网站。

7．3．3　经验研究

1．相关指标的描述性统计值

表7．8显示了2002～2010年28个制造业行业主要指标的描述性统计分析结果。

表7．8　描述性统计检验

注：RDSR指研发投入占销售收入比重；NUM指行业中企业数量；EXPR指出口交货额占销售收入比重；ALR指资产负债率；LAR指流动资产比率；LMYR指大中型企业比重；KL 指资本-劳动比率（对数）。

由表7．8可见，在考察期内，各主要指标存在较大的差异。工业增加值的最大值和最小值相差100多倍，资产规模的差异超过12倍，而劳动的差异超过了50倍。工业品出厂价格和加权资产价格与上年同比既有上升也有下降。行业间工资的差异超过了12倍。

2．行业全要素生产率和行业实际汇率的估计结果

我们运用ODonnell（2010）的方法估算了28个制造业行业的全要素生产率，根据Goldberg（2004）的方法估算了各行业的实际汇率。表7．9显示了28个制造业行业全要素生产率和行业实际汇率变动率的平均值、中间值和标准差。

表7．9　制造业行业全要素生产率和行业实际汇率变动率的主要统计指标（2002～2010）

续　表

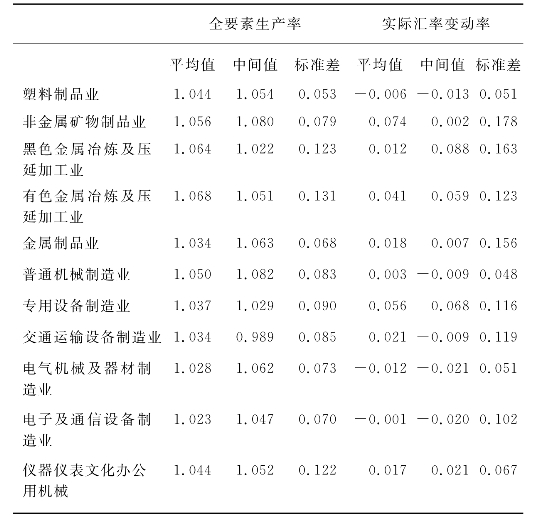
由表7．9可见，2002～2010年，各行业全要素生产率指数的平均值大于1，说明中国制造业行业存在较明显技术进步（涂正革和肖耿，2005；张海洋，2005；李小平和朱钟棣，2006）。在所有行业里，烟草制品业的全要素生产率平均值和中间值都最高，而石油加工及炼焦业的全要素生产率最低，仅为1．013。单从统计数据来看，烟草制品业是最具优势的行业（常亚青和宋来，2006）。有色金属冶炼及压延加工业全要素生产率波动性最高，其标准差达到0．131，文教体育用品制造业波动最低，仅为0．025。

此外，对于多数行业来说，2002～2010年的实际汇率变化率的平均值都大于0，说明实际汇率数值上升，行业实际汇率出现了贬值。2005年人民币汇率形成机制改革以来，人民币相对美元大幅升值，但美元相对欧元、日元和英镑等主要货币波动较为复杂，再加上中国和主要贸易伙伴国物价水平的走势也不相同，因而实际汇率与对美元名义汇率的走势并不一致。在所有行业里，木材加工及木、竹、藤、棕、草制品业的实际汇率变化率的平均值最大，达到0．150，说明该行业的实际汇率贬值幅度最大，有利于出口。电气机械及器材制造业的实际汇率变动率的平均值和中间值都小于0，说明该行业实际汇率升值，不利于产品出口。从标准差来看，各个行业实际汇率在2002～2010年的变动幅度并不相同。

我们接下来分析28个制造业行业全要素生产率和行业实际汇率是否存在显著的行业差异。如果存在显著差异，说明本书采用行业实际汇率作为汇率指标效果更好。传统的多样本差异性检验方法是方差分析方法，该方法要求样本具有齐方差性、独立性等前提条件。但是，行业实际汇率都受到名义汇率的影响，存在一定的相关性，不满足方差分析的前提条件，因此，本节采用非参数检验，即Friedman检验方法，检验结果见表7．10。

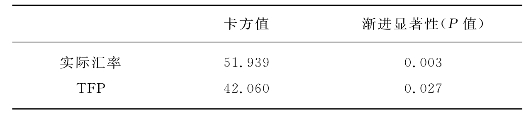
表7．10　分行业实际汇率和全要素生产率的Friedman检验结果

注：自由度为27。

表7．10中实际汇率和全要素生产率的Friedman检验值分别为51．939和42．060，分别在1%和5%的水平上显著，说明中国28个制造业行业的实际汇率和全要素生产率存在显著差异，利用行业实际汇率指标能更加客观地反映行业间的差异。

3．面板数据模型分析

为了避免模型在拟合过程中出现多重共线性问题，我们对自变量进行相关分析，结果见表7．11。

表7．11中相关分析结果表明，相关系数都小于0．7，主要指标之间并不存在高度相关关系。本节采用这些指标作为自变量，不会产生多重共线性问题。

我们先分别运用截面—时间固定效应最小二乘法（OLS）和广义矩（GMM）方法对所有28个制造业行业的全样本数据，利用Eviews6．0软件拟合（7．34）式，回归结果见表7．12。

表7．12　全样本数据估计结果

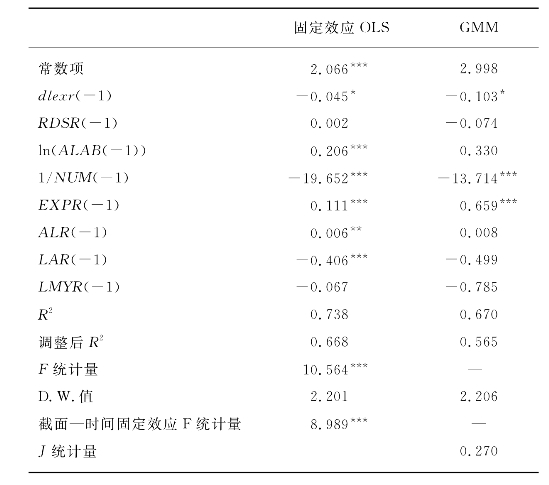
注：回归模型的因变量为全要素生产率（TFP），自变量为行业实际汇率变动率（dlexr）、行业研发支出占销售比率（RDSR）、行业平均员工数的对数［ln（ALAB）］、行业中企业数量的倒数（1／NUM）、行业出口交货额占销售额之比（EXPR）、行业资产负债率（ALR）、行业流动资产占总资产比率（LAR）和行业中大中企业工业增加值在全行业中占比（LMYR），所有自变量均滞后一年（－1）。

由表7．12可见，用两种方法估算的全样本模型中，调整后R2都超过了50%，说明模型具有一定的解释力。OLS估计结果中，F统计量可以在1%的水平上通过显著性检验，说明模型所反映的变量关系成立。截面—时间固定效应F统计量也可以在1%的水平上通过检验，证明了模型存在截面和时间固定效应。在两个模型中，D．W．值都表明模型的残差不存在自相关性。在GMM模型中，J统计量说明本书选择的工具变量是有效的，采用GMM方法可以有效地克服模型的内生性问题，其估计结果比OLS方法更有效。在两个模型中，除研发指标外，其他系数的符号都相同。行业实际汇率变动率的系数小于0，但仅在10%的水平上通过显著性检验，显著性不好，可能是因为实际汇率的影响在不同类型行业中存在差异，需要利用分组样本做进一步分析。

我们根据行业资本-劳动比率的不同将所有行业分为高比率组和低比率组，分别运用固定效应OLS方法和GMM方法，利用Eviews6．0软件进行估算，结果见表7．13^[5]。调整后R2显示，两个模型的拟合效果都较好，模型的解释力较高。OLS固定效应模型的F统计量说明变量之间的关系成立，GMM模型的J统计量说明模型中的工具变量的选择较为合理。因此，以下将着重分析GMM模型的结果。

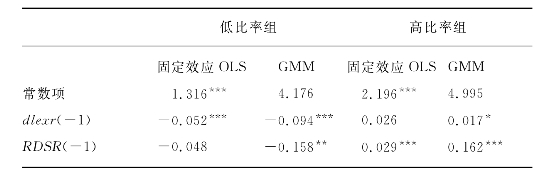
表7．13　分组检验结果

续　表

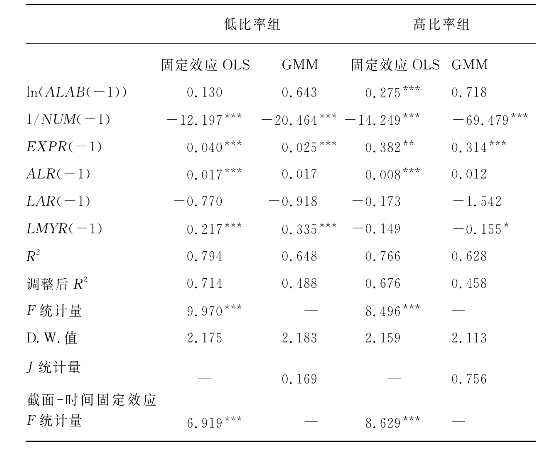
表7．13的回归结果显示了行业实际汇率对不同资本-劳动比率行业组技术进步的影响。在低比率样本组，上一年行业实际汇率变化率（dlexr）的拟合系数在OLS固定效应模型和GMM模型中都很显著，在资本劳动比率较低的行业中，行业实际汇率的变动能够影响行业的全要素生产率。GMM模型中行业实际汇率的回归系数为－0．094，说明在其他因素不变的情况下，行业实际汇率升值速度上升1倍，低资本-劳动比率行业的全要素生产率将增长0．094。相反，在高比率样本组，上一年行业实际汇率变化率（dlexr）的拟合系数都大于0，但显著性不好，说明行业实际汇率变化对高资本-劳动比率行业的技术进步的影响并不显著。

由表7．13结果可见，汇率调整能够在一定程度上促进制造业技术进步，但是对制造业技术进步的影响是有条件的，受行业的资本-劳动比率影响。资产和高技能劳动的专用性较高，低技能劳动的专用性程度相对较低（Hainmueller　＆Hiscox，2007）。如果制造业多为劳动密集型行业，低技能劳动比重大，那么企业对资本的依赖度就不高。现有机器设备不多，在技术更新过程中现有机器设备折旧及报废造成的损失就不大，企业进行技术更新投资所产生的资本调整成本就会较小。在人民币升值导致行业实际汇率适度的升值的情况下，为了应对日益加剧的国际市场竞争，企业有可能增加技术更新资本投入，有效地促进制造业行业的技术进步（Leung　＆Yuen，2010）。但是，在高资本-劳动比率组别里，由于企业现有机器设备价值较大，技术更新投资过程中的资本调整成本较高，因此，行业实际汇率变动后，资本调整成本过高，增加技术更新投入的动力不足，全要素生产率受到的影响并不显著。汇率调整对劳动密集型行业的影响更大，这一结果证明了理论模型的结论，也与现有研究结论基本一致（袁堂军，2009；马君潞等，2010）。

此外，在高比率样本组中，研发投入比率（RDSR）能够在1%的水平上通过系数显著性检验，且回归系数大于0，说明在高资本-劳动比率行业中，加强研发能够有效地促进行业技术进步。在低比率样本组中，大中企业比重（LMYR）能够通过系数显著性检验，且回归系数大于0，说明在资本-劳动比率较低的行业中，大中型企业越多就越有利于行业的技术进步，因此企业规模是影响低资本-劳动比率行业技术进步的关键因素之一。在两个组别的回归结果中，反映行业竞争度的企业数量倒数（1／NUM）和出口比率（EXPR）等指标的回归系数都能够通过显著性检验，这两个变量的回归系数说明低竞争和高出口比重能够促进行业全要素生产率的提升。从回归系数的符号可见，企业数量越多、竞争度越高，越不利于全要素生产率的提升。出口比率的系数大于0，说明出口比重大的行业技术进步速度也越快，出口越活跃的行业越有可能通过技术外溢效应实现全要素生产率的提升（Bernard　＆Jensen，1995）。

4．稳健性检验

我们再利用Eviews6．0软件就行业实际汇率对制造业技术升级的非对称性影响机制进行稳健性检验，表7．14显示了利用交叉项进行的稳健性检验结果。

表7．14　稳健性检验

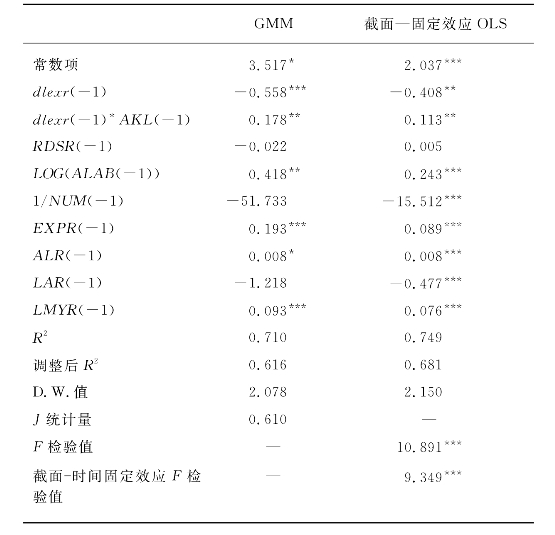
由GMM分析的J统计量可见，GMM模型更有效。行业实际汇率项（dlexr）及其与行业平均资本-劳动比率交叉项［dlexr（－1）＊AKL（－1）］的回归系数能够通过系数显著性检验，且汇率项的回归系数小于0，与表7．12一致。同时，汇率交叉项与汇率的回归系数符号相反，说明随着行业平均资本-劳动比率的变化，行业实际汇率对行业全要素生产率具有非对称性影响。

经验分析结果显示，中国制造业行业的实际汇率对行业全要素生产率具有显著的影响，实际汇率对全要素生产率的作用机制受制造业行业的资本-劳动比率影响，具有非对称性特征。在资本-劳动比率低的劳动密集型行业，适度升值可以促进技术进步。

7．3．4　简要结论

人民币汇率制度改革和制造业产业升级是当前中国经济发展中的重要课题，能否在人民币汇率制度改革的背景下有效地促进制造业产业升级，将直接影响中国发展为制造业强国的进程，具有极其重要的理论价值和现实意义。

本节在现有研究的基础上，构建了包含技术更新资本和生产制造资本的生产函数，考虑了资本调整成本，分析了企业利润最大化时汇率调整对技术水平的影响机制，并运用中国的数据测算了行业实际汇率，运用经验分析方法研究了人民币实际汇率对中国制造业技术进步的影响。研究结果发现，汇率对制造业技术进步具有显著的影响，但是其影响具有行业特征。资本密集型行业资本-劳动比率高，对资本依赖大，资本调整成本更高，人民币升值对资本密集型行业的技术进步的作用不显著。相比之下，人民币适度升值对劳动密集型行业的技术进步具有一定的推动作用。

在当前情况下，要协调人民币汇率体制改革和制造业发展战略，促进制造业技术进步，必须做到以下几点。第一，汇率体制改革必须考虑到制造业的行业特征。不同的行业在人民币升值过程中表现也不同，在设计汇率体制改革方案时，必须充分考虑到中国制造业行业的具体差异，通盘考虑汇率制度改革对不同行业的影响。减少人民币升值对资本密集型行业的负面影响，同时，为劳动密集型行业的技术进步创造良好的外部条件。第二，利用贸易结构调整战略化解人民币名义汇率调整的不利影响。在当前国际经济环境动荡不安的情况下，既要保证贸易对象的适度稳定，更要灵活调整贸易对象的结构，才能有效调节行业实际汇率，促进制造业技术进步。第三，创造良好的政策环境，鼓励资本-劳动比率高的制造业行业加快研发投入，促进技术进步。经验研究表明，研发投入的增加对高资本—劳动比率的制造业行业全要素生产率的提升具有积极影响，应当大力发展科技金融，通过税收优惠、低息贷款和科技创新基金等多种方式向这些行业提供技术更新资本，实现技术升级。第四，国际贸易能够对制造业行业全要素生产率产生正的溢出效应，制造业行业应当积极融入国际市场，通过国际贸易促进自身的技术进步。此外，还要根据制造业行业的具体特征，避免重复投资造成的过度竞争，促进制造业的适度集中，增强制造业企业实现技术升级的能力。