的面板数据

一、概述

伴随着房地产业的蓬勃发展，房地产投资占全社会固定资产投资比重过高、房价暴涨、金融融资渠道单一、银行信贷风险加大等一系列问题开始涌现出来，这里面最突出的问题就是始于2003年以来全国房价水平的大幅上涨。虽然国家先后出台了许多相关政策，但是房价仍然处于高位运行状态，日益高涨的房价显然超出了中国广大人民的购买力水平，住房已经成为“生命中不可承受之重”。根据吕江林（2010）的研究，2006—2008年三年我国35个大中城市的房价收入比平均为9.71、10.63、10.06，其中北京市最高，三年分别为15.55、19.59、19.58，远远超过国际公认3—6年的合理标准。究竟是什么原因导致了房价的暴涨？社会上有些人把它归因于高地价，特别是国土资源部2002年5月9日《招标拍卖挂牌出让国有土地使用权规定》和2004年3月31日《关于继续开展经营性土地使用权招标拍卖挂牌出让情况执法监察工作的通知》（即著名的“8·31”大限）政策的先后出台，明令商业、旅游、娱乐和商品住宅等各类经营性用地必须以招标、拍卖或者挂牌方式出让，即自2004年8月31日后不得再以历史遗留问题为由采用协议方式出让经营性土地使用权。

由于实行土地招拍挂以后，土地出让费用的大幅上涨与房价飞涨的时期基本一致，自然就得出了在房价中占30%左右比例的地价上涨从而使建筑成本上升，导致房屋最终销售价格不断攀升的结论。特别值得一提的是，持这种观点的人主要以中国房地产业协会的杨慎（2003）、包宗华（2004）和以陈淮（2004）为主的建设部课题组为代表，他们认为正是由于在土地交易时大量采用了价高者得的拍卖方式，导致地价激增从而拉动房价的飞涨，这一“成本推动论”的观点自然也得到了以华远集团总裁任志强为首的广大开发商的拥护。与之相反的是国土资源部的观点，时任副部长的贠小苏（2006）认为，经营建设用地的招拍挂虽然导致地价上涨，但却不一定抬升了房价，影响房价最重要的要素是房屋市场的供求关系，土地是房地产业的一个生产要素，对土地的需求是由对房屋需求产生的引致需求。正是由于房屋市场上的供不应求，房价上涨使得开发商对土地需求增加，拉动了地价上涨，这一“需求拉动论”的观点与“成本推动论”形成了鲜明对比，双方似乎都想把造成房价上涨的原因推给对方，对于这个类似于究竟是“鸡生蛋”还是“蛋生鸡”的问题，吸引了国内外一大批学者对其进行了深入的研究。

这个问题同样也在国内学者中同样也引起了很大的争论，绝大多数学者都认为房价和地价在长期内互为因果，其中以严金海（2006）、郑娟而和吴次芳（2006）、宋勃和高波（2007）为代表。分歧主要在短期，如况伟大（2005）、郑娟而和吴次芳（2006），他们都认为短期内房价与地价也相互作用；而严金海（2006）则认为短期内房价决定地价，宋勃和高波（2007）却认为短期内地价影响房价。国内学者的上述研究大都采用全国层面的季度时间序列数据，从1998年中国房地产市场化改革到2008年，最多也不过10年40个样本。由于样本容量有限，该方法的可信度又大打折扣。更重要的是，房地产市场是个具有浓重地方色彩的区域性市场，不同地区房价的决定因素是不同的，地价对房价的影响方式和大小也不尽相同，采用国家层面的时序数据就不能体现中国各个不同地区的异质性，这是在研究方法上的一个重大缺陷。因此研究房地产问题，最好采用分地区的面板数据。值得一提的是，黄静和屠梅曾（2009）采用全国29个大中城市1999—2008年的季度面板数据检验了房价与地价之间的因果关系，但是他们使用的数据仍然是来自《中国经济景气月报》的房屋销售价格指数和土地交易价格指数，由于这个是季度同比指标，只能反映某一个地区房价和地价纵向时间序列变化，而不能进行同期的横向比较^[12]，因此也不能完全反映房地产价格的区域差异，这也是他们利用面板协整DOLS估计出来各城市的地价弹性差异悬殊的一个很重要原因，因而本书有必要用合理的面板数据来研究房价与地价的因果关系问题。

二、房价与地价相互关系的一个简单模型

在进行计量检验之前，本书导出了一个房价与地价之间的函数关系式，为后面的计量模型设定提供一定的参考。该模型参考了Brueckner（1986）的研究框架，假设存在这么一个住房生产函数Q（L，K），其中Q为住房建筑面积，L、K分别为建筑房屋所投入的土地、资本等生产要素，在Brueckner（1986）的模型中，该住房生产函数有以下三个特点：①土地与资本两种生产要素之间具有完全替代性，地价上升，可以通过减少土地投入并增加资本投入使得产出水平保持不变。②规模报酬不变，即Q（tL，tK）＝t Q（L，K）。③QK（K，L）＞0，QKK（K，L）＜0，QL（K，L）＞0，QLL（K，L）＜0，一阶导数为正说明资本与土地的边际产出为正，二阶导数为负说明资本与土地的边际产出递减，同时这个条件也保证了利润函数有最大值。

一个代表性开发商的目标函数为：

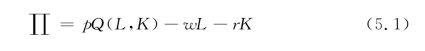
其中∏为利润，p、w分别为每单位面积的住房价格、土地价格，r为每单位资本的价格，也可以简化为利率。开发商通过选择最优的资本投入K和土地投入L来最大化利润∏。此时，最优的资本投入K和土地投入L取决于土地的价格w和资本的价格r。

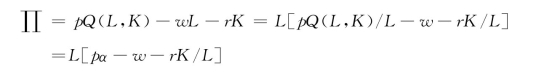
这里的α为容积率，它等于住房建筑面积除以建筑所使用的土地面积，即α＝Q（L，K）／L。由于住房生产函数具有规模报酬不变的特点，则：

k为单位土地面积的资本存量，则开发商的利润函数为：

此时问题转化为开发商选择一个最优的容积率α使得利润最大化，对（5.3）式求一阶条件，则有：

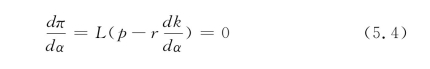
在完全竞争的市场条件下^[13]，开发商的利润为0，故：

联立（5.2）、（5.4）、（5.5）三式，可以解出容积率：

从（5.6）式可以看出，最优容积率α与住房生产函数Q、土地价格w和利率r有关。给定具体的生产函数，容积率就取决于w和r。当地价上升时，由于资本和土地具有完全替代性，这时就可以通过减少土地投入并增加资本投入使得建筑面积保持不变，从而提高了容积率，这也是Peng and Wheaton（1994）的观点。所以是地价影响容积率，而不是容积率决定地价（丁成日，2008）。给定地价和利率，开发商通过选择土地和资本的最优投入水平（进而决定了容积率）使利润最大化。

由于不知道住房生产函数Q（k）的具体形式，（5.6）式只能得到α关于w，r，Q的隐式解，同样地将（5.6）式代入（5.5）式，消去α也无法得到p与w和r之间的显式解。要想清楚地揭示房价与地价、利率之间的函数关系，则必须给出Q（k）的具体数学表达式。在这里我们假设：

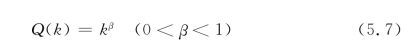
此时开发商的利润函数变成∏＝＝L［p kβ－w－rk］。由于k和α具有（5.2）式的函数关系，为了计算方便，因此转而对k而不是对α求一阶导数，有：

（5.9）式就是反映房价与地价、利率之间关系的数学表达式，房价与地价、利率之间是对数加权平均的关系，这也是本书后面进行实证检验的基本方程式。其中房价对地价的弹性为1－β，这是个小于1的正数，说明地价上涨导致房价以相对较小的幅度上涨。正是由于地价的上升幅度更大，导致当地价上升时，地价在房价中所占的比例也随之上升，这一点得到了实际数据的验证。1998年我国房地产市场化改革以来，地价平均以每年10%的速度上涨，地价在房价中所占的比例也由1998年的18.1%一路上升到2008年的31.2%^[14]。可以预见，随着地价的上涨，地价在房价中所占的比例将会越来越大。

三、实证检验

（一）数据说明和变量选取

本书计量的全部数据都来源于中经网统计数据库，时间跨度从2002年3月—2008年6月，由于西藏自治区、青海省、海南省三省（区、市）的数据缺失较多，所以选取去掉这三个省（区、市）后剩下28个省（区、市）作为截面的面板数据^[15]。由于中经网没有直接公布全国各地区每个月的房价和地价指标，只有按月统计的本年购置土地面积＿累计（单位万平方米）、房地产开发中土地购置费投资总额＿累计（单位亿元）、商品房销售额＿累计（单位亿元）、商品房销售面积＿累计（单位万平方米），因此在本书中是按照如下公式计算的：

当月地价＝（本月本年房地产开发中土地购置费投资总额＿累计

　　　　　－上月本年房地产开发中土地购置费投资总额＿累计／

　　　　　本月本年购置土地面积＿累计

　　　　　－上月本年购置土地面积＿累计）×10 000

房价也采用类似方法计算。由于每年没有公布一月份相关数据，所以二月份计算数据其实是一、二两个月的平均水平，这样每年实际只有11个月数据。同时每个省都没有2007年10月的数据，这样一来，2007年又损失了两个月数据。所以总共实际有68个月的数据，理论上应该有68×28＝1 904个样本。去掉其中一些明显的异常值和某些地区在某些时间的缺失值以后，得到的是一个非平衡面板数据。由于这种数据是房地产价格的绝对值，而不是黄静和屠梅曾（2009）所使用的房地产价格指数的相对值，因而在不同地区之间就有了横向可比性。

从表5.12可以看出，各地在2002年3月—2008年6月的平均地价水平798.8元可以占到房价2 640.1元的30.3%。同时地价与房价的标准差也很大，说明各地区各个时期的房价和地价水平是处于巨大波动当中的。房地产市场的一个很明显特征就是区域的异质性，不同地区房地产价格的差异是非常大的。因此本书从全国31个省（区、市）中选取几个比较有代表性的省（市），他们是东部的北京市（BJ）、上海市（SH）、广东省（GD），中部的江西省（JX）和湖南省（HN），西部的贵州省（GZ）与新疆维吾尔自治区（XJ），对它们的房价与地价分别作图表示。

表5.12　变量的描述性统计

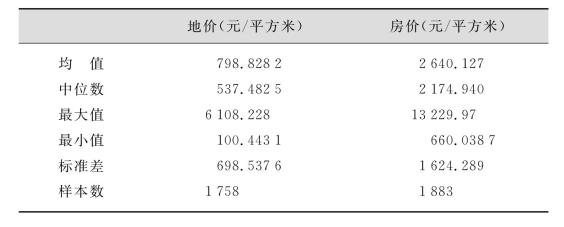
图5.5表示的是房价随时间的变化情况，图5.6表示的是地价变动情况。中间间断是由于统计数据的缺失或者属于明显的异常值被剔除了。从图5.5、图5.6中可以看出，相比于房价有着明显随时间向上的趋势，地价的时间趋势不是那么明显，忽上忽下，呈现出周期性变化，但是总体趋势仍然还是上升的。无论是房价还是地价，东部地区北京市、上海市、广东省的变动幅度都特别大，而且始终在高位运行，而西部地区贵州省与新疆维吾尔自治区几乎没有什么变化，且价格也始终处在一个较低的水平，中部地区湖南省和江西省的价格水平和变化幅度处于前面两者之间。这些都说明了我国的房地产价格的区域差异是非常明显的，因此采用面板数据模型进行研究是非常必要的。

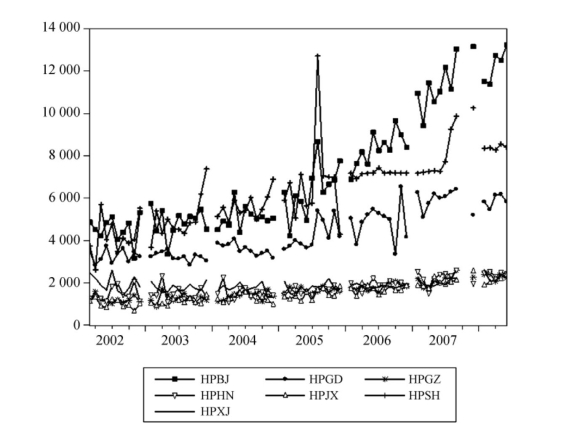
图5.5　代表性地区房价变化图

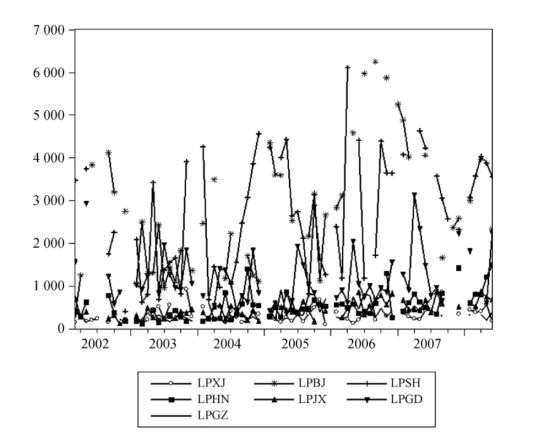
图5.6　代表性地区地价变化图

注：以上数据来源于中经网统计数据库，并根据作者整理所得。

（二）房价分布滞后模型估计结果

前面推导出的房价与地价之间的关系式为：

本书计量模型的设定以此为基础，由于各个开发商向银行的借款利率差别不大，因此可以把它视为常数，计量方程变为：

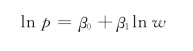
Peng and Wheaton（1994）等人的相关研究表明当期地价往往是对一到两年后的房价发生显著影响，因此在这里也引用了若干期的滞后地价作为解释变量，采用分布滞后模型的形式。为了体现土地招拍挂制度和房地产市场的区域差异的影响，随后还引入了相关虚拟变量作为控制变量进行回归。房价hp和地价lp在下面的回归和检验时都取了自然对数（下面都用小写字母表示取自然对数后的变量），见表5.13。

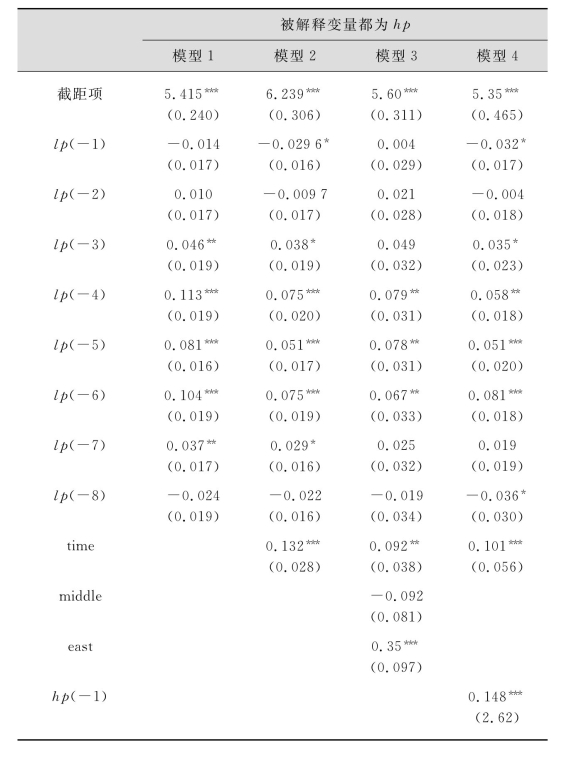
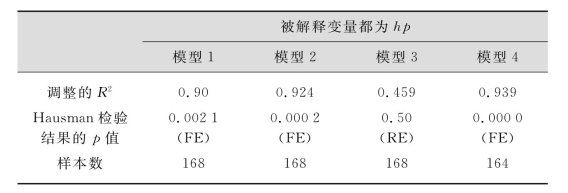
表5.13　模型估计结果

续　表

注：（1）＊＊＊表示该变量在1%的显著性水平上显著，＊＊表示在5%的显著性水平上显著，＊表示在10%的显著性水平上显著。
（2）每个变量的估计值下报告的是面板稳健性标准差（PCSE）。
（3）通过Hausman检验选择相应估计形式。其中FE表示固定效应模型，RE表示随机效应模型，并采用了截面加权广义最小二乘估计以克服各截面之间可能存在的异方差。

在模型1中，只是对滞后1—8期的地价进行回归^[16]，结果第1、2两期的系数都不显著，第3—7期的系数都比较显著，特别是第4、5、6三期估计出来地价对房价的弹性值平均在10%左右，这说明：在短期内，地价并不影响房价，但是在长期中，地价是会对房价产生一定影响。随着“8·31”大限政策的出台，要求从2004年8月31日以后所有经营建设用地都必须以招拍挂形式出让。为了分析这一政策对房价的影响效果，在模型2中引入了一个时间虚拟变量（time），让2004年9月以后的各个月份都取1，结果该变量在1%的显著性水平上显著，其估计结果显示土地招拍挂制度实施后，全国房价水平平均上涨了13.2%^[17]。为了进一步考察各地区房价水平的差异，在模型3中以西部地区作为对照组，选取了中部和东部两个地区虚拟变量，结果东部地区虚拟变量也是非常显著，其值显示在控制住地价水平的前提下，由于经济基本面因素的作用（如物价水平、人均收入等）使东部地区房价的平均水平比西部高出了35%，这也是非常符合实际情况的。中部地区虚拟变量估计出来的系数为负，但是不显著。一个可能的原因是由于在西部地区的样本中剔除了经济发展水平最落后的西藏自治区和排名也比较靠后的青海省后，同时包括经济在全国都比较发达的四川省、重庆市，在经济基本面的作用下，使西部和中部的房价水平整体体现不出多大差异。这一点从图5.5和图5.6中也可以大致判断出，作为中部代表的湖南省和江西省与西部代表的贵州省与新疆维吾尔自治区四省（区、市）的房价都在2 000元上下波动。最后在模型4中加入了上一期的房价水平，结果该变量显著异于0，并显示上一期的房价以14.8%的变化程度影响现在的房价水平，表明房价的变化遵循较强的适应性预期。

（三）基于面板误差修正模型的Granger因果关系检验

在上面通过加入地价滞后期的几个模型回归结果都有两个特点：第一，在模型3和4中分别加入了地区虚拟变量和上一期的房价，反映土地招拍挂效果的时间虚拟变量都是非常显著的，而且其估计出来的结果也变化不大，平均都在10%左右，说明这个结果是非常稳健的，土地招拍挂制度的实施确实对房价上升造成了一定的影响。第二，在所有4个模型中，滞后第1、2两期的系数基本都不显著，从第3期开始变得显著，但是估计出来的弹性值很小。第4、5、6期都在5%显著性水平以下通过变量显著性检验，而且其系数也都比较大，平均在8%左右，这些都能够在一定程度说明在短期内地价不影响房价，在长期内地价才会对房价产生作用。但是为了更清楚地验证两者之间的相互关系，必须使用由Granger（1969）提出的Granger因果关系检验。为了避免“伪回归”，在做因果关系检验前，必须进行相关的单位根和协整检验。

在面板数据中主要有五种单位根检验方法，分别是：LLC检验（Levin、Lin and Chu，2002）、IPS检验（Im、Pesaran and Shin，2003）、Breitung检验、Fisher检验（包括ADF和PP检验）和Hadri检验（Hadri，2000）。其中LLC检验、Breitung检验和Hadri检验是假设面板数据中各截面序列具有相同单位根过程。而IPS检验、Fisher检验面板数据中各截面序列具有不同单位根过程。其中只有Hadri检验类似于时间序列中的KPSS检验，原假设是面板数据中各截面序列都不含有单位根。为了保证结果的稳健性，这里采用了分别包含同质面板的LLC检验和异质面板的ADF－Fisher检验。由于房价和地价数据都有着随时间变化的趋势，因而在对原变量进行单位根检验时，都选择带有截距项和时间趋势项形式，在对其一阶差分变量进行单位根检验时则采用不带有任何截距项和时间趋势项形式。由于时间跨度比较长，有68个月的月度数据，因此在检验时选择了较长的滞后期，结合样本等多方面的因素，在这里选择最大滞后期为6，具体阶数由软件根据sic准则自动选取。

表5.14　面板单位根检验结果

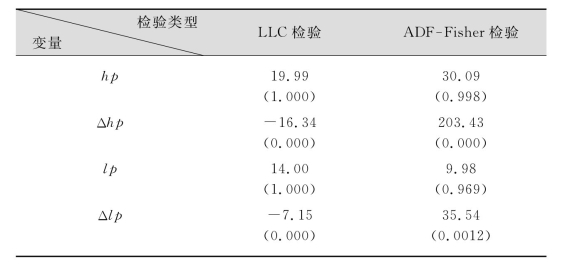
注：报告的结果都是该检验对应统计量的值，下边括号里的数字表示其相伴概率。

从该结果可以发现房价和地价都存在单位根，其一阶差分变量都是平稳的，说明房价和地价都是I（1）变量。为了检验其在长期中是否存在均衡关系，本书还有必要对这两个变量继续进行协整检验。

面板数据的协整检验方法可以分为两大类：一类是原假设为不存在协整关系，使用类似Engle and Granger（1987）平稳回归方程，从面板数据中得到残差构造统计量进行检验，如Pedroni（1999）、Kao（1999）就属于类似分析；另一类是Maddala and Wu（1999）基于Fisher所提出的单个因变量联合检验结论，该方法通过联合单个截面个体Johansen协整检验的结果获得对应于面板数据的检验统计量。本书选择的是Pedroni检验，同样才进行检验时也采用了带有时间趋势项的形式，最大滞后阶数也为6，具体阶数由软件根据sic准则自动选取，见表5.15。

表5.15　面板协整检验结果

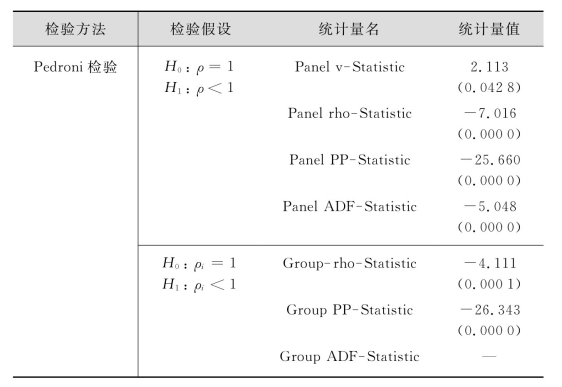
注：前四个统计量主要检验同质面板的协整关系，后三个统计量主要检验异质面板的协整关系。统计量值下边括号里的数字表示其相伴概率。

上述各个统计量都拒绝了不存在协整关系的原假设，但是变量之间有协整关系只能告诉我们变量之间存在着长期因果关系，但不知道因果关系的具体方向。Pesaran and Smith（1995）、Pesaran、Shin and Smith（1997，1999）等提出了面板误差修正模型的估计方法，也是采用类似Engle and Granger（1987）提出的EG两步法，第一步先估计出其对应的自回归分布滞后模型（ARDL）：

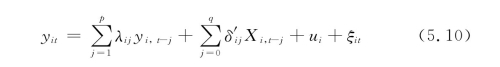
第二步则得到如下误差修正模型：

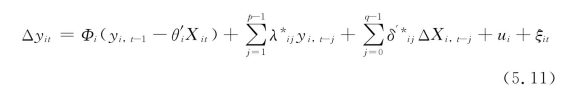
上式中Φi代表误差修正项的调整系数，如果显著为负，说明变量之间确实存在恢复到长期均衡的关系，也就是通常所说的协整关系。X是各解释变量的向量集合，如果其中某个解释变量前面的系数δi1＝δi2＝…＝δiq－1＝0，则说明该解释变量不是被解释变量的短期Granger原因。对于（5.11）式，Pesaran and Smith（1995）、Pesaran、Shin and Smith（1997，1999）先后提出了MG（mean－group）和PMG（pooled mean－group）估计方法，两者的共同之处都是短期系数δij都随个体发生变化，不同的是PMG估计中的长期系数θ不随个体发生变化，本书采用长、短期系数都不随个体发生变化的dynamic fixed effect方法进行估计^[18]。综合样本大小和实际经济情况，最大滞后阶数p选择4，为了保证结果的稳健性，本书也对滞后3、5阶的情况进行估计，结果也没有很大不会，在估计的时候同时考虑了其截面相关性。

参照梁云芳、高铁梅（2007）的研究，考虑到中国各个地区房地产价格波动的差异性，除了对全国进行全样本检验以外，还分别对东部、中部、西部进行分地区的考察。上面三式中的下标j＝0，1，2，3，分别代表全国、东部、中部和西部，i＝1，2…，28，代表中国的28个省（区、市），t＝1，2，…，68，代表从2002年3月到2008年6月之间的68个有效月度。

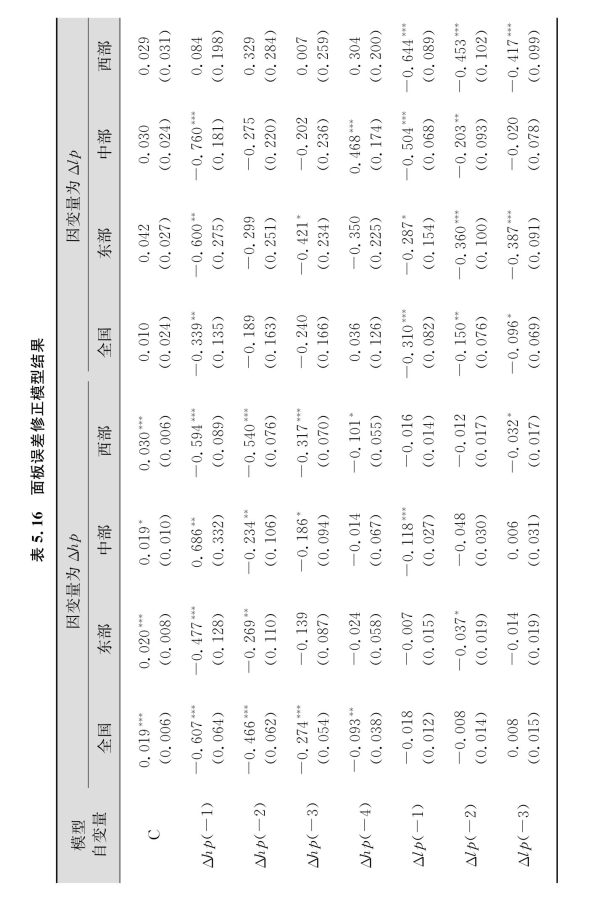
在上面地价与房价的双向因果关系检验中，除了在因变量为Δhp时，东部的误差修正项不显著以外，其他模型的误差修正项基本都在1%的显著性水平（只有在因变量为Δlp时，西部是在10%的水平）上通过变量显著性检验。这说明除了在东部，地价不是房价的长期Granger原因以外，其他地区长期中房价和地价都是互为长期Granger原因。这主要是由于在东部房地产市场上一直以来都存在着较为严重的投机泡沫，房价预期主导着该地区的住房市场（况伟大，2008）。本书在以东部地区为样本对模型4进行估计发现，上一期的房价每提高1%，导致本期的房价提高0.5%^[19]，这说明在东部房价表现出非常强的自回归性。在短期中，只有中部地区的地价非常明显地表现为房价的短期Granger原因，而房价都基本是地价的短期Granger原因（虽然东部地区在10%的显著性水平上没有通过检验，但是如果能够稍微放松点显著性水平，由于其对应的p值为0.116，在12%的显著性水平下，房价在短期内还是存在着对地价的影响）。之所以只有中部地区的地价表现为房价的短期Granger原因，一个很可能的原因就是虽然国家提出了中部崛起战略，但是由于现阶段中央政府的财政支出重点还是在西部，因而对中部地区财政支持力度不够。为了筹集经济发展的大量资金，这些地区的地方政府在土地出让中较大比例采取了价高者得的拍卖形式，而中央政府出于发展当地地方经济，扩大地方政府财政收入的角度考虑，往往默许了这一举措，从而导致了地价激增在短期内也推动了房价的上涨。本书同样也以中部地区为样本对模型2进行回归发现，这时时间虚拟变量前的系数非常大，其值显示由于土地招拍挂制度的实施使得中部地区的房价提高了21.1%，远远超过全国13.2%的平均水平。综上所述，在全国范围来看，无论是长期还是短期，房价都基本表现为地价的Granger原因，说明房价对地价的需求拉动作用明显。地价对房价的成本推动作用在短期还不是很明显，而在长期中地价确实推动了房价的上涨。

综上所述，本书从估计房价对地价弹性和检验两者之间的因果关系两方面进行了实证研究。首先利用2009年7月25日国土资源部对外正式公布的全国30个省（区、市）、87个城市、536个楼盘调查数据，对我国的房价与地价关系进行了十分细致的实证研究。再通过统计分析发现我国房地产价格存在着十分明显的区域差异，这种差异不仅仅局限在东部与中部和西部之间的区间差异，更体现在每个地区大城市与中小城市的区内差异，随后本书对影响房价的因素（特别是地价）进行了计量检验。从全国来看，地价每上涨1%，将导致房价上涨0.355%，这个结果是高度稳健的，基于分位数回归、空间计量、截断回归均得到了与之十分接近的结果。分区域来看，地价弹性在中部和西部之间差距不明显，而东部则要高出中部和西部许多。而同样是经济发达地区的大城市地价弹性却要比中小城市低，此时地价对房价影响程度体现出了较为明显的区域间差异。进一步深入到各地区各城市之间，这种区内差异体现得更为明显，西部中小城市地价弹性比西部大城市低了0.1个百分点。地价弹性最高是东部中小城市，其次是中部大城市、西部大城市、中部中小城市，东部大城市地价弹性仅高于西部中小城市。随后本书利用2002年3月—2008年6月中国28个省的面板数据，采用Pesaran、Shin and Smith（1997，1999）提出的面板误差修正模型方法对房价与地价的因果关系进行了检验，证实了在全国范围内，无论是长期还是短期，房价都表现为地价的Granger原因，因此房价对地价的需求拉动作用明显，而地价只是房价的长期Granger原因，因而地价对房价的成本推动作用主要还是体现在长期中。就不同地区而言，东部地区的地价不是房价的长期Granger原因，中部地区的地价非常明显地表现为房价的短期Granger原因，西部地区只有地价不是房价的短期Granger原因。

【注释】

[1]该节主要内容出自王岳龙，“地价对房价影响程度区域差异的实证分析”，《南方经济》，2011年第3期。

[2]利用这三年中国统计年鉴中的商品房销售额除以商品房销售面积计算得到。

[3]这里之所以没有按照房地产业中通常所说“一线城市”“二线城市”和“三线城市”进行划分，一个最主要的原因就是目前上述分类在业内还是一个很模糊的概念，尚未形成有说服力的具体分类标准。

[4]这里东部是指北京、福建、广东、江苏、辽宁、山东、河北、上海、天津、浙江、海南10省（区、市）；中部地区包括：安徽、河南、山西、黑龙江、湖南、湖北、吉林、江西、内蒙古9省（区、市）；西部地区包括：甘肃、广西、贵州、宁夏、新疆、云南、四川、重庆、陕西、西藏、青海11省（区、市），后面都按照这个标准划分。

[5]由于本书是一个由不同土地出让时间、不同地区的楼盘所堆积在一起的混合截面数据，估计的时候为了控制不同地区、不同时间的影响，采用类似面板数据固定效应虚拟变量最小二乘法的原理，设置了若干地区和时间虚拟变量，因此在估计时把这些虚拟变量都以加法形式引入模型。如果要体现地区和时间差异，本书则采用进一步分子样本回归的方法，而不是以乘法形式设置虚拟变量与相应变量的交叉项进行估计，这样能够有效避免虚拟变量设置过多的问题。

[6]该结论的证明可查阅伍德里奇，《计量经济学导论：现代观点》（第二版），中译本，中国人民大学出版社，第85页。

[7]对于形如lny＝a＋bx这样的半对数模型，伍德里奇，《计量经济学导论：现代观点》（第二版），中译本，第185页中提出了如下关系式：%Δy＝100·［exp（b）－1］，这个b就是x每增加一个单位使y提高100［exp（b）－1］个百分点的半弹性，以下同，并且直接报告根据估计系数算出来的半弹性值。

[8]2006—2008年出让土地的楼盘售价均值分别为5 247元／平方米、4 548.7元／平方米和3 605.5元／平方米，2008年拿地的楼盘售价较之2006年下降了近30%，这个与估计下降24.1%很接近。

[9]Chow　test除了在时间序列模型中用来检验是否存在稳定的结构参数，还可以用来比较两组截面数据的回归模型是否存在差异。在伍德里奇，《计量经济学导论：现代观点》（第二版），中译本，第222页，给出了一个用该方法检验男女之间的学习成绩影响因素是否存在差别的例子。

[10]stall manual，stata press在stata11的手册中提供了一个劳动力市场方面的例子，在250个妇女的子样本中，其中有150个有工作，而100个没有工作。如果只是为了考虑有工作的妇女其工作时间的影响因素，这个时候采用去掉100个没有工作妇女样本的OLS估计方法更有效。如果不考虑是否有工作对工作时间的影响，这个时候用截断回归模型更有效。

[11]该节主要内容出自王岳龙、张瑜，“基于中国省级面板数据的房价与地价关系研究”，《山西财经大学学报》，2010年第1期。

[12]举个例子，如果2008年1季度上海市的房价季度同比指数为105，贵阳市为110，这就说明上海2008年1季度的房价是2007年1季度房价的1.05倍，贵阳市是1.1倍，只能说2008年1季度贵阳市房价增速高于上海市。但是不能由此认为贵阳市房价已经超过了上海市。

[13]现实生活中的房地产市场是个高度寡占的市场，在这里看成是完全竞争市场，是一种基于长期中的理想化假定，即在长期中房地产市场的进入壁垒最终消失，企业自由进出最后将导致0利润的结果。Smith（1976）建立了一个与本书十分类似的模型，也是假设开发商的利润在长期中满足零利润的条件。

[14]作者根据中国资讯行公布的数据计算得到。

[15]研究房地产最好是以城市一级的数据作样本，但是考虑到数据的可得性，城市往往只有年度数据。由于Granger因果关系检验通常需要较长的时期，所以在这里只好选择了省级面板数据。考虑到2008年下半年度以来全球金融危机对房地产业带来的不利影响，本书将其后的样本给剔除了。由于本书样本已经足够大，因而不会产生很大影响。

[16]这里之所以选择到第8期，是因为从第7期开始地价开始变得不是很显著，而第8期的系数不显著地为负，说明太多滞后项导致变量之间的多重共线性问题比较严重，故在回归时只取到滞后第8期。这也说明了相比与外国的房地产市场，我国土地价格的变化对房价的反应更加迅速。

[17]这个其实就是王松涛（2008）加入土地招拍挂时间虚拟变量的方法，由于没有有效分离出干预序列，因而其估计系数并不是政策实际影响效果，只能简单说土地招拍挂制度实施以后的这段时间，房价变化了多少。

[18]关于面板误差修正模型的理论和软件操作方面的详细介绍，可以参考Edward F.Blackburne Mark W.Frank，Estimation of nonstationary heterogeneous panels，Stata Journal 2007，Vol.7，1ss.2，pp.197－208。

[19]在况伟大（2008）的研究中该值为更大的0.73%，笔者认为这个差异主要还是由于选择的样本区间和解释变量不同造成的。