总体风险限额的确定

保险公司总体风险限额反映了保险公司可以承受的最大资产损失的大小。作为开端，保险公司董事会和风险管理委员会应当主持确定一个合适的总体风险限额。保险公司总体风险限额的确定是一个复杂的工作，它需要依赖各个方面的信息，这些信息主要包括：公司的资本实力、股东的风险偏好、宏观经济条件、监管要求、公司的收益以及对公司过去所有风险的判断与估计等。

图5-2保险公司风险限额管理过程

目前，确定保险公司总体风险限额的方法主要有以下几种。

(1)专家判断法。根据内部和外部风险管理人员的知识和经验。

(2)构建模型法。①指标判断法：基于统计数据和统计方法。②期权模型法：将保险公司看成是一种期权。③动态财务分析法。

(3)混合模型。结合专家判断法和期权模型法。

一、专家判断法确定保险公司总体风险限额

早期确定总体风险限额的方法主要依赖于主观判断，也就是说，不经过任何精确的计算，而只是靠公司董事会、风险管理人员和风险管理专家的经验和知识对总体风险限额做出的一种合理但是主观的评估，其中，风险管理专家可以是企业内部的风险管理人员，也可以是来自外部的风险管理人员。用于评估总体风险限额的专家判断系统可以归纳为以下几个方面：公司资本实力，即公司能够支付损失的财务能力;股东的风险偏好，即股东承担风险的意愿;周期，即未来市场的宏观经济条件;监管要求，即监管机构对保险公司承担风险的要求，通常而言，监管机构不愿意保险公司承担过度风险;特性，即保险公司的收益状况和风险状况。尽管风险限额各个指标的评估是由公司董事会、风险管理人员和风险管理专家进行，但是经常出现不一致性和主观化这些问题。而且传统的专家判断法无法预测企业的违约概率。所以专家判断法存在着很多问题，主要包括以下几个方面。

(1)做出决策的过程存在主观性和随意性，不同的专家可能对相关信息做出不同的判断，这些判断甚至可能导致截然不同的决策。

(2)决策过程除了学徒方式，不存在其他有效的培训方式。

(3)确定总体风险限额的过程是非自动化的，操作过程比较慢，与风险限额管理要求实时动态调整的目标不符，尤其在内外部条件发生急剧变化时，专家判断法很难做出及时反映。

但是，尽管构建模型法在风险限额模型中的应用变得更加广泛，但是专家判断法还是在总体风险限额确定中扮演了重要角色。其原因是多方面的，例如，小样本的统计分析在总体风险限额模型中存在很多问题，如预测的过度拟合、缺少观察值造成变量系数的不稳定等。在这种情况下，专家判断方法因为较好地反映了风险管理专家对公司风险的判断经验，显得更有代表性。

二、指标判别法确定保险公司总体风险限额

指标判别法是保险公司广泛应用的总体风险限额确定方法。运用指标判别法确定保险公司总体风险限额，首先需要建立与保险公司总体风险限额相关的指标体系。指标体系的建立又包括风险限额指标的初选和风险限额指标的筛选两个步骤。通常而言，选取的指标要有代表性、实用性和可操作性，能够很好地反映保险公司整体风险的状况。近些年来，尤其是2008年世界性金融危机的爆发，使人们越来越意识到操作风险和业务风险的重要性，因此，在指标的选取中，除了包含市场风险、承保风险、信用风险等风险状况的指标外，还应该包含操作风险的相关指标。常见的判别指标可以由表5-1表示。

指标体系建立之后，接下来需要做的就是建立风险限额的指标判别系统。判别系统的核心是寻找合适的统计方法，最常见的方法是首先使用聚类分析方法提取因子，然后使用主成分分析方法得到提取因子的得分系数矩阵，最后通过变量标准化方法计算得出因子的得分。随着遗传算法和人工神经网络方法的引进，也可以建立基于遗传算法和人工神经网络的判别系统(张维功等，2009;刘洪渭等，2009)。

指标判别系统建立之后，就可以运用已有数据得到各指标的权重，并据此预测保险公司的总体风险限额。基于指标判别法的保险公司总体风险限额确定过程可以用图5-3表示。

指标判别法可以有效解决保险公司总体风险限额确定过程中的主观性和随意性，具有更强的实用价值和参考价值。保险公司在完成构建总体风险限额指标判别系统后，可以根据实时数据更新已有的总体风险限额数据，因此具有更强的时效性。指标判别法同专家判断法一样，不能通过指标判别法确定公司的违约概率。另外，指标判别法的精确度与指标的选取息息相关，完善的指标体系可以产生良好的预测效果，对于不完善的指标体系会降低预测的效果，甚至会导致灾难性的后果。与保险公司相关的指标成百上千，要准确找到与总体风险限额相关的指标是相当困难和繁琐的工作，需要相关人员具有扎实的理论基础和丰富的实践经验。

表5-1可用于保险公司指标判别体系的代表性指标

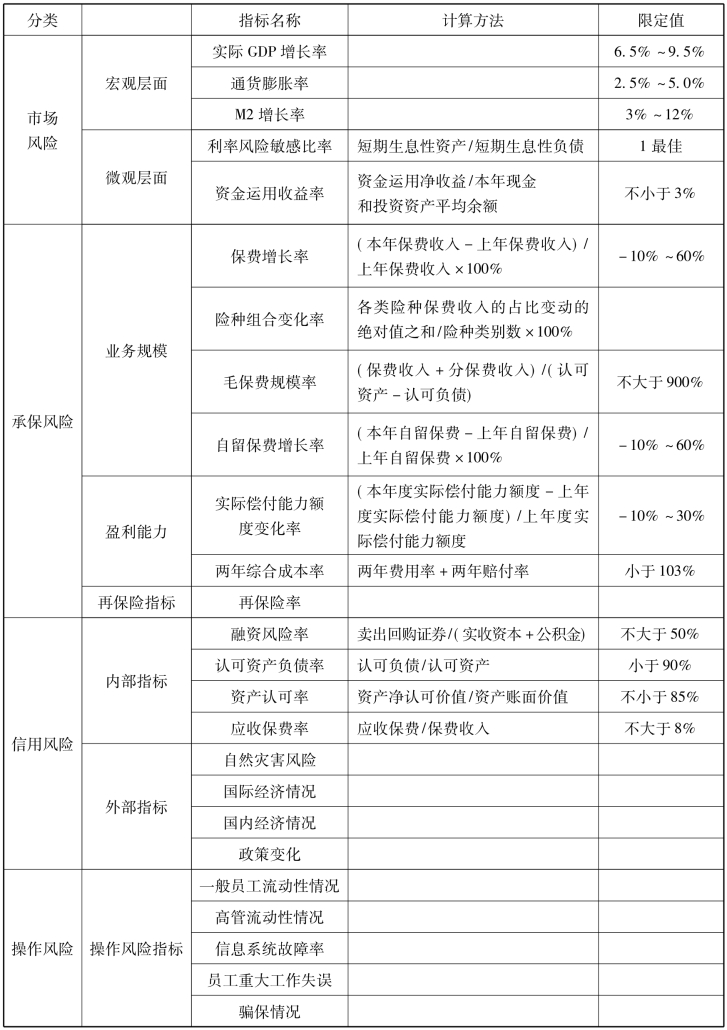
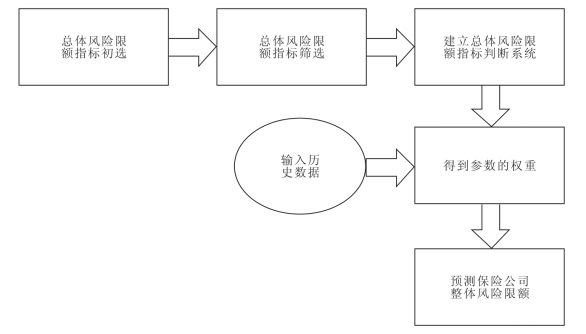
图5-3保险公司基于指标判别法的总体风险限额确定过程

三、期权模型法确定保险公司总体风险限额

目前，期权模型法正被越来越多的保险公司所采用。期权模型可以克服专家判断法和指标判别法的相关缺陷，正逐渐成为保险公司确定总体风险限额的主流。期权模型法主要是将保险公司看成是一个期权，如Merton(1974)年提出的默顿模型。根据默顿模型，保险公司股东实际上拥有的是一个看涨期权(Call Option)，由式(2-10)可以得到总体经济资本限额为：

虽然，默顿模型在实践中获得了广泛的应用，如穆迪KMV成功开发出了KMV模型，其判断违约概率的方法便是使用默顿模型。但是应该看到默顿模型还存在不完善的地方，有学者认为不能只将保险公司看成是一个看涨期权，而应该将保险公司的资产和负债看成两个期权，因此公司的净资产可以看成是一个置换期权(Myers、Read，2001)。作为对默顿模型的改进，本部分将保险公司的资产和负债看成两个期权，运用置换期权相关理论研究保险公司总体风险限额。

设保险公司在年初的资产价值为V0，保险公司的总损失为L0，则保险公司的净资产为E0，E0=V0-L0。到年末时，记该保险公司的资产价值为V1，总损失为L1。如果到年末时，公司的资产价值V1大于或等于L1，则公司所有者拥有V1-L1的权益价值;若V1小于或等于L1，则公司的所有者权益价值为0，因此年末时保险公司的净资本额为：

假设保险公司的资产和负债均服从下述Ito过程：

其中，d Z1和d Z2为维纳过程，d Z1和d Z2之间的相关系数为ρ12。进一步假设α1、α2、v1、v2为常数。

不难看出，保险公司所有者权益E(Vt，Lt，t)实际上是欧式期权，该期权的价值至少为0，且不小于t时刻的资产V1，即：

期权购买者在t时刻可以通过出售ω1≡∂E/∂Vt单位的资产，同时购买-ω2≡-∂E/∂Lt单位的负债对冲风险。定价公式E(·)必须是对Lt、Vt而言是线性齐次的，运用欧拉定理可得：

运用McKean(1969)中的方法，可得：

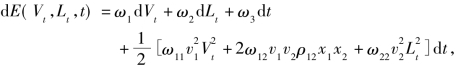
其中，ω3=∂E(Vt，Lt，t)/∂t。

结合式(5-8)和式(5-9)可得：

反解方程(5-10)，可以得到欧式期权E(V t，Lt， t)的定价公式为：

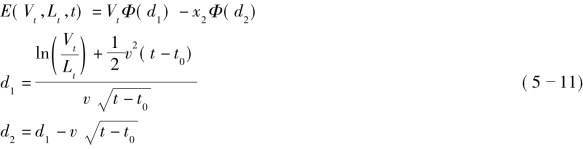
其中，Φ(·)是标准正态分布的累积概率函数;的方差; Φ(d2)为在风险中性世界中执行该欧式期权的概率，同时这个概率也是期权到执行时刻t时，保险公司资产价值大于负债价值的概率P(Vt≥Lt)。显然，当公司资产Vt小于负债价值的概率PD=P(Vt＜Lt)为：

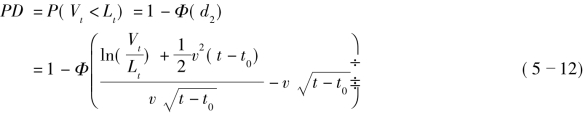
经过简单推导，容易得到∂PD/∂v＞0，说明保险公司出现破产的概率随着企业所有者权益波动率的增加而增加，并且违约概率PD与所有者权益的波动率v的关系是一一对应的。

进一步对式(5-12)进行求解，可得：

根据式(5-13)可以看出，当给定执行期(t0，t］结束时的资产估计值Vt，容忍概率PD，资产和负债波动率v1、v2，d Z1和d Z2之间的相关系数为ρ12，就可以得到t时刻企业的净资产。如果假设企业不能从外部获得资本，那么企业能够使用的最大资本量就是E(Vt，Lt，t)，即保险公司总体风险限额Et就是E(Vt，Lt，t)^[1]。

类似穆迪KMV公司提出的违约距离(Distance to Default)，同样可以定义违约距离为资产价格偏离违约点的距离占标准差的倍数，违约距离的定义为：

当违约距离减少时，保险公司出现违约的可能性加大;反之，当违约距离增加时，保险公司出现违约的可能性降低。在实际应用中，可以对违约距离设定不同的等级(也称为关卡)，针对不同的等级采取不同的行动。

四、动态财务分析法确定保险公司总体风险限额

无论期权模型法是将保险公司看成一个看涨期权，还是看成一个置换期权，都对资产和(或)负债的分布特征进行了限定，即假定它们服从对数正态分布，在这点上，理论界是存在争议的。Kneuer(2003)、Ruhm和Mango(2003)、Vrieze和Brehm(2003)、Mildenhall(2004)分析了期权模型使用的前提条件，以及期权模型的局限性。对期权模型最广泛的质疑就是有关分布函数的假设。通常情况下，当保险公司业务处于较稳定状态时，运用期权模型可以很好地估计保险公司的总体风险限额;而对于业务快速发展的保险公司而言，期权模型法并不能反映保险公司业务增长的特征。

针对期权模型法在确定保险公司总体风险限额方法存在的局限性，本项目提出可以使用动态财务分析法(Dynamic Financial Analysis，DFA)确定保险公司总体风险限额。Eling等(2008)、Eling和Toplek(2009)较早将DFA模型应用于保险公司的财务分析，本项目所使用的DFA模型就是以Eling等(2008)、Eling和Toplek(2009)的模型为基础。

令ECt表示保险公司在时期t，t∈{1，2，…，T}的权益资本，Et表示保险公司在时刻t的收益，则保险公司的权益资本ECt可以表示为：

其中，max((It+Ut)·tr，0)表示当(It+Ut)·tr＞0时，max((It+Ut)·tr，0)=(It+Ut)·tr;当(It+Ut)·tr＜0时，max((It+Ut)·tr，0)=0。

保险公司在配置资产时，可以将资产配置于无风险资产(银行存款和国债投资)和风险资产，其中无风险资产的比例和收益率分别为αt-1(αt-1∈(0，1］)和r1t，风险资产的比例和收益率分别为1-αt-1和r2t。保险公司总体投资收益率rpt和投资收益It分别可以表示为：

保险公司在时刻t的收益Et主要是由两个部分组成的：投资收益It和承保收益Ut。假设保险公司面临的税率为tr，则保险公司的收益Et可以表示为：其中，Pt-1表示保费收入;k表示可投资资金的比例，是外生变量，小于等于1，且大于等于0。

接下来需要估计保险公司的保费收入。在保费预测中，关键是要对保费收入的周期性进行刻画，Cummins和Outreville(1987)、Eling和Toplek(2009)认为保险市场存在承保周期，并运用一个含有二阶滞后项的向量自回归模型估计。借用Cummins和Outreville(1987)、Eling和Toplek(2009)的模型，设∏t 为保费水平：

保险公司的保费收入由两个方面决定：承保周期和消费者反映函数。消费者反映函数(cr)主要是由保费水平和保险公司偿付能力决定。令MV表示整个保险市场的承保金额，βt-1表示保险公司所占市场份额。则保费收入Pt-1可以表示为：

保险公司的成本用综合费用表示，并记为Exct。综合费用通常是索赔金额C的一个固定比例，记为δ，即：

在对保险公司承保业务进行分类时，可以将保险公司的业务分为高风险承保业务和低风险承保业务。高风险承保业务和低风险承保业务赔付率分别记为l1t和l2t，所占份额分别为βt-1和1-βt-1(βt-1∈(0，1］)，则总索赔损失C可以表示为：

因此承保收益Ut为：

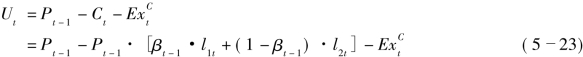
在非寿险公司动态财务分析模型中，关键是要刻画不同风险之间的相关关系，最常见的方法是假设资产与负债均服从正态分布，并使用线性相关关系刻画资产与负债之间的相关关系，然而也有研究表明资产与负债之间存在非线性关系(Eling、Toplek，2009)。最常见的刻画不同随机变量之间非线性关系的方法是Copula方法(McNeil et al，2005;Demarta、McNeil，2005;Embrechts，2009)。

为了在财产保险公司DFA模型中刻画低风险投资、高风险投资、高风险承保业务和低风险承保业务之间的相关关系，引入4种不同的Copula函数，它们分别为四维Gauss Copula函数、四维T Copula函数和两种四维不可互换Archimedean Copula函数(Clayton Copula函数和Frank Copula函数)(Sun et al，2008;SCOR Switzerland AG，2008;Eling、Toplek，2009)。

Gauss Copula函数、T Copula函数和四维不可互换Archimedean Copula函数可分别表示为下式。

(1)四维Gauss Copula函数：

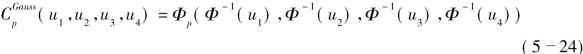
其中，Φ(·)表示标准正态分布的分布函数;Φ-1(·)表示标准正态分布的逆分布函数。

(2)四维T Copula函数：

其中，tv，p(·)表示相关系数矩阵为p，自由度为v的标准四元t分布函数。

(3)四维不可互换Archimedean Copula函数：

其中，φ称为Archimedean Copula函数的生成元，不同的Archimedean Copula函数可以由不同的生成元构成，其中Clayton Copula函数和Frank Copula函数的生成元及主要性质见表5-2。

表5-2 Archimedean Copula函数的主要性质

假设保险公司能够容忍的风险水平为α，则保险公司所能容忍的最大风险损失为：

即：

其中，F1(r1t)、F2(r2t)、G1(l1t)、G2(l2t)分别表示低风险投资收益率、高风险投资收益率、低风险承保业务赔付率和高风险承保业务赔付率的边缘分布函数;C(·)表示四维Copula函数，Ω={(r1t，r2t，l1t，l2t)|ECt(r1t，r2t，l1t，l2t)＜0}。

则保险公司能够容忍的风险水平为α时，保险公司的风险限额P Limit为：

反解方程(5-28)并结合公式(5-29)，就可以得到总体风险限额的值。在实际应用中通常是将Monte Carlo方法得到总体风险限额的近似值。运用Monte Carlo方法估计总体风险限额的近似值包括以下几个步骤。

(1)运用极大似然法、两阶段极大似然法等估计风险随机变量的相关关系和Copula参数值。

(2)根据相关关系和Copula参数值，运用Monte Carlo方法产生N个分位数值，通常N= 100 000。

(3)对产生的N个分位数值按照从小到大的顺序进行排序，第(1-α)N个值即为估计得到的在险价值VaRα(ECt)的值。

(4)计算权益资本的期望值E(ECt)，用第三步得到的在险价值VaRα(ECt)的值减去权益资本的期望值E(ECt)即为保险公司的风险限额P Limit。